Задача розв'язування
|
Read other articles:

Proklamasi Penghapusan Perbudakan di Koloni Prancis, 27 April 1848, 1849, oleh François Auguste Biard, Istana Versailles Penghapusan perbudakan terjadi pada waktu yang berbeda di berbagai negara. Penghapusan ini sering terjadi secara berurutan dengan lebih dari satu tahap – misalnya, penghapusan perdagangan budak di negara tertentu, dan kemudian dilanjutkan dengan penghapusan perbudakan di seluruh kerajaan atau kekaisaran. Setiap langkah penghapusan ini biasanya merupakan hasil dari hukum ...

Bagian dari seriPaleontologi Fosil Fosilisasi Fosil jejak (Ichnofosil) Mikrofosil Persiapan fosil Fosil indeks Daftar Fosil Daftar situs fosil Lagerstätte Daftar Fosil peralihan Daftar fosil evolusi manusia Sejarah alam Biogeografi Kepunahan massal Geokronologi Skala waktu geologi Catatan geologis Sejarah kehidupan Abiogenesis Garis waktu evolusi makhluk hidup Fosil transisi Evolusi dari berbagai Organ tubuh Terbang pada burung Sel Multisel Mata Flagela Rambut Evolusi mosaik Sistem syaraf Se...
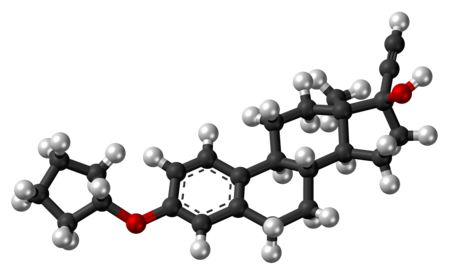
Pharmaceutical drug QuinestrolClinical dataTrade namesEstrovis, othersOther namesQuinoestrol; Quinestrenol; Quinoestrenol; Ethinylestradiol 3-cyclopentyl ether; EECPE; EE2CPE; W-3566; 3-(Cyclopentyloxy)-17α-ethynylestra-1,3,5(10)-trien-17β-olAHFS/Drugs.comMicromedex Detailed Consumer InformationRoutes ofadministrationBy mouthDrug classEstrogen; Estrogen etherATC codeNonePharmacokinetic dataElimination half-life>120 hours (>5 days)[1]Identifiers IUPAC name (8R,9S,13S,14S,17R)-3...

Okura Museum of Art大倉集古館Exhibition Hall (1927) by Itō Chūta; reinforced concrete with bronze roof; Registered Cultural PropertyAlternative namesŌkura ShūkokanGeneral informationAddress2-10-3 ToranomonTown or cityMinato, TokyoCountryJapanCoordinates35°40′1″N 139°44′36″E / 35.66694°N 139.74333°E / 35.66694; 139.74333OpenedAugust 1917 / October 1928Design and constructionArchitect(s)Itō ChūtaArchitecture firmŌkura DobokuWebsiteshukokan.org Oku...

United States historic placeAgricultural Heating stationU.S. National Register of Historic Places Agricultural Heating StationLocation1535 Observatory Dr., Univ. of WI, Madison, WisconsinCoordinates43°04′34″N 89°24′42″W / 43.07611°N 89.41167°W / 43.07611; -89.41167 (Agricultural Heating station)Arealess than one acreArchitectJohn T.W. JenningsArchitectural styleRichardsonian RomanesqueNRHP reference No.85000570[1]Added to NRHP...

Monumen Penjelajahan (Padrão dos Descobrimentos) Monumen (Monumento) Nama asal: padrão dos descobrimentos dalam bahasa Portugis berarti penanda penjelajahan Negara Portugal Region Lisboa Sub-region Grande Lisboa Kabupaten Lisboa Munisipalitas Lisboa Lokasi Santa Maria de Belém - elevasi 50 m (164 ft) - koordinat Panjang 46 m (151 ft), Utara-Selatan Lebar 20 m (66 ft), Barat-Timur Tinggi 52 m (171 ft) Kedalaman 20 m (66 f...

Voce principale: L.R. Vicenza Virtus. L.R. Vicenza VirtusStagione 2018-2019Sport calcio Squadra Vicenza Allenatore Giovanni Colella (1ª-19ª) Michele Serena (20ª-28ª) Giovanni Colella (29ª-38ª e play-off) All. in seconda Moreno Greco (1ª-19ª giornata) Davide Zanon (20ª-28ª giornata) Moreno Greco (29ª-38ª) Presidente Stefano Rosso Serie C8º posto (ai playoff) Coppa Italia2º turno Coppa Italia Serie CSemifinale Maggiori presenzeCampionato: Zonta, Grandi (27)Totale: Zonta (36)...

Pour les articles homonymes, voir Gongué et Agogo (Ghana). Cet article est une ébauche concernant la musique traditionnelle. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Agogô à quatre cloches. L'agogô, gã ou gongué est un instrument de musique d'origine africaine. C'est un instrument de percussion idiophone constitué d'une ou plusieurs cloches en bois ou en métal (sans battant), reliées entre elles...

Pura Taman AyunPintu masuk bangunan ke pusatInformasi umumGaya arsitekturCandi HinduAlamatMengwi, Kabupaten Badung, BaliNegaraIndonesiaMulai dibangun1632Rampung1634Desain dan konstruksiArsitekTan Hu Cin Jin Situs Warisan Dunia UNESCONama resmiLanskap kultur Provinsi Bali: Sistem subak sebagai perwujudan dari filosofi Tri Hita KaranaJenisBudayaKriteriaii, iii, v, viDitetapkan2012 (sesi ke- 36)No. referensi1194NegaraIndonesiaKawasanAsia-Pasifik Pura Taman Ayun merupakan Pura Paibon/Pedarma...

Kebenaran artikel ini dipertanyakan. Kemungkinan isinya berupa hoaks. Harap verifikasi sumber tepercaya yang digunakan di artikel atau bagian-bagiannya, serta tambahkan sumber tepercaya pada klaim yang tidak ada rujukannya. Jika rujukannya tidak tepercaya, cobalah mengusulkan artikel ini untuk dihapus dan/atau menghapus bagian yang dipertanyakan. Jika halaman ini terang-terangan merupakan hoaks, tambahkan {{db-hoax}} agar dapat dihapus dengan cepat. Silakan bicarakan halam...

UK political publisher This article is about the publisher. For the Malaysian animal rights campaign, see Bite Back. Biteback PublishingFounded2009Country of originUnited KingdomHeadquarters locationHullDistributionMarston Book Services (UK)Consortium Book Sales & Distribution (US)NewSouth Books (Australia)Pansing Distribution (Singapore)[1]Publication typesBooksImprintsThe Robson PressOfficial websitewww.bitebackpublishing.com Biteback Publishing is a British publisher based in H...

1899 battle of the Second Boer War Battle of ElandslaagtePart of Second Boer WarPositions at noon, before the battleDate21 October 1899LocationElandslaagte, KwaZulu-Natal, South Africa28°24′S 29°57′E / 28.400°S 29.950°E / -28.400; 29.950 (Battle of Elandslaagte)Result British victoryBelligerents United Kingdom South African RepublicCommanders and leaders John FrenchIan Hamilton Johannes Kock †Adolf SchielStrength 3,50018 guns[1] 1,...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

31st Miss Universe pageant Miss Universe 1982Date26 July 1982PresentersBob BarkerJoan Van ArkEntertainmentRex SmithJosé Luis RodríguezVenueColiseo Amauta, Lima, PeruBroadcasterCBS (international)Panamericana (official broadcaster)Entrants77Placements12DebutsNew CaledoniaWithdrawalsCyprusFijiGibraltarSt. KittsTahitiReturnsEl SalvadorIndonesiaPapua New GuineaSt. MaartenSurinameWinnerKaren Dianne Baldwin CanadaCongenialityMaureen Lewis Cayman IslandsBest National CostumeMaría Fran...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

South Korean footballer and manager An Ik-soo An in December 2021Personal informationFull name An Ik-sooDate of birth (1965-05-06) 6 May 1965 (age 59)Place of birth South KoreaHeight 1.83 m (6 ft 0 in)Position(s) Centre-backCollege careerYears Team Apps (Gls)1985 Incheon National University Senior career*Years Team Apps (Gls)1986–1987 Sangmu FC (draft) 1988 Kookmin Bank 1989–1995 Ilhwa Chunma 142 (1)1996–1998 Pohang Steelers 58 (0)Total 200 (1)International career199...

Overview of the foreign relations of Cyprus Politics of Cyprus Constitution Cyprus dispute Law of Cyprus Taxation Executive President Nikos Christodoulides Council of Ministers (Cabinet) Legislative House of Representatives President: Annita Demetriou Judiciary Supreme Court of Cyprus Elections Presidential: 20182023 Legislative: 201120162021 European: 201420192024 List of Political Parties Administrative divisions Famagusta Kyrenia Larnaca Limassol Nicosia Paphos Foreign relations Diplomatic...

Period of Romania under the Soviet occupation Part of a series on the History of Romania Prehistory Cucuteni–Trypillia culture Hamangia culture Bronze Age in Romania Prehistory of Transylvania Antiquity Dacia Dacian Wars Roman Dacia Origin of the Romanians Middle Ages (Early) History of Transylvania Banat in the Middle Ages First Bulgarian Empire Second Bulgarian Empire Voivodeship of Maramureș Founding of Wallachia Founding of Moldavia Rumelia Eyalet Early Modern Times Silistra Eyalet Pri...