Простий вузол (теорія вузлів)

В теорії вузлів простий вузол або просте зачеплення — вузол, який, у певному сенсі, нерозкладний. Точніше, це нетривіальний вузол, який не можна подати у вигляді конкатенації двох нетривіальних вузлів. Про вузли, які не є простими, кажуть як про складені вузли або складені зачеплення. Визначити, чи є даний вузол простим чи ні, може виявитися складною задачею.

Приклади

Хорошим прикладом сімейства простих вузлів служать торичні вузли. Ці вузли утворюються шляхом накручування кола на тор p разів в одному напрямку і q разів в іншому, де p і q є взаємно простими цілими числами.

Найпростіший простий вузол — це трилисник з трьома перетинами. Трилисник є, фактично, (2, 3)-торичним вузлом. Вузол «вісімка» з чотирма перетинами є найпростішим неторичним вузлом. Для будь-якого додатного цілого числа n є скінченне число простих вузлів з n перетинами. Перші кілька значень числа простих вузлів (послідовність A002863 з Онлайн енциклопедії послідовностей цілих чисел, OEIS) подані в таблиці.

n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Число простих вузлів
з n перетинами 		0 0 1 1 2 3 7 21 49 165 552 2176 9988 46 972 253 293 1 388 705
Складені вузли 0 0 0 0 0 2 1 4 … … … …
Всього 0 0 1 1 2 5 8 25 … … … …

Зауважимо, що антиподи враховувалися в цій таблиці і на малюнку нижче тільки один раз (тобто вузол і його дзеркальне відображення вважаються еквівалентними).

Зображення всіх простих вузлів з сімома і менше перетинами без урахування дзеркальних відображень. (Тривіальний вузол простим не вважається)

Теорема Шуберта

Теорема, що належить Хорсту Шуберту, стверджує, що будь-який вузол можна єдиним чином подати у вигляді конкатенації простих вузлів[1].

Див. також

Примітки

  1. ↑ Schubert, 1949, с. 57—104.

Література

  • H. Schubert. Die eindeutige Zerlegbarkeit eines Knotens in Primknoten // S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. — 1949.

Посилання

  • Weisstein, Eric W. Prime Knot(англ.) на сайті Wolfram MathWorld.
  • [Prime Links with a Non-Prime Component] Атлас вузлів (англ.)

Read other articles:

Kepler-9

Kepler-9 Lukisan artistik mengenai Kepler-9, termasuk planet Kepler-9b dan c Data pengamatan Epos J2000      Ekuinoks J2000 Rasi bintang Lyra[1] Asensio rekta  19j 2m 17.7544d[2] Deklinasi  +38° 24′ 03.177″[2] Magnitudo tampak (V) 13.9[3] AstrometriGerak diri (μ) RA: 2,491±0,028[2] mdb/thn Dek.: −14,713±0,032[2] mdb/thn Paralaks (π)1,5629±0,017...

 

Muhammad Quraish Shihab

Al-Habib Muhammad Quraish ShihabPotret Quraish Shihab sebagai Menteri Agama Indonesia Menteri Agama Indonesia ke-16Masa jabatan14 Maret 1998 – 21 Mei 1998PresidenSoeharto PendahuluTarmizi TaherPenggantiAbdul Malik FadjarRektor UIN Syarif Hidayatullah Jakarta ke-8Masa jabatan1992–1998 PendahuluAhmad SyadaliPenggantiAhmad Sukardja Informasi pribadiLahir16 Februari 1944 (umur 80)Sidenreng Rappang, Celebes, Hindia Belanda masa pendudukan JepangSuami/istriFatmawati Assega...

 

Pedra de Lume

Pedra de LumePedra de LumeKoordinat: 16°45′47″N 22°53′42″W / 16.763°N 22.895°W / 16.763; -22.895Koordinat: 16°45′47″N 22°53′42″W / 16.763°N 22.895°W / 16.763; -22.895Negara Tanjung VerdePulauSalMunisipalitasSalParoki sipilNossa Senhora das DoresKetinggian3 m (10 ft)Populasi (2010)[1] • Total329 Pedra de Lume adalah sebuah desa di bagian timur laut pulau Sal, Tanjung Verde. Desa ini ...

George Hamilton (aktor)

George HamiltonHamilton pada Agustus 2009LahirGeorge Stevens Hamilton12 Agustus 1939 (umur 84)Memphis, Tennessee, A.S.Tempat tinggalPalm Beach, Florida, A.S.PekerjaanAktorTahun aktif1952–sekarangSuami/istriAlana Stewart ​ ​(m. 1972; c. 1975)​PasanganKimberly Blackford (1997–1999)AnakAshley Hamilton (l. 1974)George Thomas Hamilton (l. 1999) George Stevens Hamilton (lahir 12 Agustus 1939) adalah seorang aktor film dan televisi Ameri...

 

Rumah Sakit Huoshenshan

Rumah Sakit Huoshenshan(火神山医院)GeografiLokasiJalan Raya Zhiyinhu, Distrik Caidian, kota Wuhan, provinsi Hubei, TiongkokKoordinatCoordinates: Unknown argument formatKoordinat: Coordinates: Unknown argument format{{#coordinates:}}: lintang salahOrganisasiPendanaanPemerintah TiongkokJenisKhususPelayananUnit Gawat DaruratVirus KoronaRanjang pasien1,000[1]SejarahDibuka22 Januari 2020 s/d 2 Februari 2020 Rumah Sakit Huoshenshan Hanzi sederhana: 火神山医院 Hanzi tradisional: �...

 

Fifth Third Field (Toledo, Ohio)

Home venue of the Toledo Mud Hens Fifth Third FieldLocation406 Washington StreetToledo, OhioUnited StatesCoordinates41°38′54″N 83°32′20″W / 41.64833°N 83.53889°W / 41.64833; -83.53889OwnerLucas CountyOperatorToledo Mud Hens Baseball Club, Inc.Capacity10,300 (8,943 fixed seats)Field sizeLeft field: 320 ft (98 m)Center field: 400 ft (120 m)Right field: 320 ft (98 m)SurfaceNatural GrassConstructionBroke groundOctober 20, 2000[...

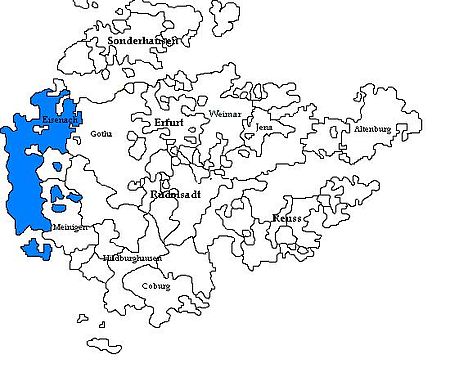
Sachsen-Eisenach

Kadipaten Sachsen-EisenachHerzogtum Sachsen-Eisenach1596–16381640–16441662–1809 Bendera Lambang   Kadipaten Sachsen-Eisenach pada 1672 (biru) di antara Negara-negara Kadipaten Ernestine yang lain di ThuringiaStatusNegara dalam Kekaisaran Romawi Suci (hingga 1806),Negara Konfederasi RhineIbu kotaEisenachPemerintahanKadipaten (Kepangeranan)Era SejarahAbad Pertengahan• Divisi Erfurt 1572• Memisahkan diri dri    S.-Coburg-Eisenach 1596• Ter...

 

Teruntum

Teruntum Lumnitzera racemosa, pelat botani menurut Blanco Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Eudikotils (tanpa takson): Rosids Ordo: Myrtales Famili: Combretaceae Genus: LumnitzeraWilld. (1803)[1] Peta persebaran Teruntum[1] Sinonim[2] Bruguiera Thouars Funckia Dennst. Petaloma Roxb. Pokornya Montrouz. Problastes Reinw. Pyrrhanthus Jack Teruntum atau Duduk (Lumnitzera ) adalah sebuah genus tumbuhan mangrove dalam famili C...

 

kartunis

Untuk orang yang membuat kartun animasi, lihat animator. KartunisKartunis Jack Elrod sedang mengerjakan halaman Minggu dari komik strip Mark TrailKomik Balon ucapan Studi komik Pendidikan Sejarah Glosarium Metode Kartun Fumetti Format Media Buku komik Strip komik Kartun editorial Kartun lelucon Novel grafik Komik web Webtoon Komik menurut Negara dan Budaya Komik Amerika Komik Belanda Komik Belgia Komik Britania Raya Komik Indonesia Komik Italia Komik Jerman Komik Kanada Komik Prancis-Belgia M...

Wressle railway station

Railway station in the East Riding of Yorkshire, England WressleGeneral informationLocationWressle, East Riding of YorkshireEnglandCoordinates53°46′23″N 0°55′26″W / 53.77292°N 0.92401°W / 53.77292; -0.92401Grid referenceSE710312Managed byNorthernPlatforms2Other informationStation codeWRSClassificationDfT category F2HistoryOpened1840Passengers2018/19 7202019/20 8662020/21 942021/22 5022022/23 494 NotesPassenger statistics from the Office of Rail and Road Wre...

 

Euripide

Disambiguazione – Se stai cercando altri significati, vedi Euripide (disambigua). (GRC) «Μνῆμα μὲν Ἑλλὰς ἅπασ᾿ Εὐριπίδου· ὀστέα δ᾿ ἴσχειγῆ Μακεδών· ᾗ γὰρ δέξατο τέρμα βίου.Πατρὶς δ' Ἑλλάδος Ἑλλάς, Ἀθῆναι· πλεῖστα δε Μούσαιςτέρψας, ἐκ πολλῶν καὶ τὸν ἔπαινον ἔχει.» (IT) «L'Ellade tutta è tomba di Euripide; ma conserva le os...

 

История христианства в Центральной Азии

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Norvège au Concours Eurovision de la chanson 2019

Norvègeau Concours Eurovision 2019 Données clés Pays  Norvège Chanson Spirit in the Sky Interprète KEiiNO Langue Anglais, Same du Nord Sélection nationale Radiodiffuseur NRK Type de sélection Melodi Grand Prix 2019 Date 2 mars 2019 Concours Eurovision de la chanson 2019 Position en demi-finale 7e (210 points, qualifiée) Position en finale 6e (331 points) 2018 2020 modifier La Norvège est l'un des quarante et un pays participants du Concours Eurovision de la chanson 2019, qui se...

 

土库曼斯坦总统

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府（Oguzkhan Presidential Palace）機關所在地阿什哈巴德任命者直接选举任期7年，可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關（英语：National Council of Turkmenistan） ...

 

Magee, Mississippi

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Magee, Mississippi – news · newspapers · books · scholar · JSTOR (July 2016) (Learn how and when to remove this message) City in Mississippi, United StatesMagee, MississippiCityDowntown Magee in March 2013 FlagLocation of Magee, MississippiMagee, MississippiLo...

Braille Without Borders

Tibet-based organization for the blind Braille Without BordersAbbreviationBWBFormation1998FounderSabriye Tenberken, Paul KronenbergFounded atLhasa, Tibet, China Braille Without Borders (BWB) is an international organisation for the blind in developing countries. It was founded in Lhasa, Tibet, by Sabriye Tenberken and Paul Kronenberg in 1998. Overview BWB's mission is to give hope and practical skills to the blind and in particular to teach braille to the blind in developing countries; if no ...

 

2016 Subic local elections

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 2016 Subic local elections – news · newspapers · books · scholar · JSTOR (August 2022) 2016 Subic local elections ← 2013 May 9, 2016 2019 →   Nominee Jay Khonghun Rolando Ampunin Heber Bascon Party SZP PDP–Laban Independen...

 

Freedom Airlines

Cet article est une ébauche concernant une compagnie aérienne et les États-Unis. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Les entreprises étant sujet à controverse, n’oubliez pas d’indiquer dans l’article les critères qui le rendent admissible. Logo der Freedom Airlines Freedom Airlines était une compagnie aérienne régionale américaine. Elle était une filiale de Mesa Air Group. Elle a cessé ses activités en 2010. Notes et références v&#...

Lee Kuan Yew

Prime Minister of Singapore from 1959 to 1990 In this Chinese name, the family name is Lee (李). The HonourableLee Kuan YewGCMG CH SPMJ DK李光耀Lee in 19751st Prime Minister of SingaporeIn office5 June 1959 – 28 November 1990MonarchsElizabeth II (1959–1963)Putra of Perlis (1963–1965)PresidentYusof IshakBenjamin ShearesDevan NairWee Kim WeeDeputyToh Chin ChyeGoh Keng SweeS. RajaratnamGoh Chok TongOng Teng CheongPreceded byOffice establishedLim Yew Hock (as Chief Mini...

 

العلاقات التوفالية الكولومبية

العلاقات التوفالية الكولومبية توفالو كولومبيا   توفالو   كولومبيا تعديل مصدري - تعديل   العلاقات التوفالية الكولومبية هي العلاقات الثنائية التي تجمع بين توفالو وكولومبيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ...