Група кіс
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Divisi Panzer Cadangan ke-273 Jerman adalah divisi tentara cadangan. Setelah Pertempuran Kursk, Divisi Panzer Cadangan ke-273 Jerman digunakan untuk memperkuat Divisi Panzer ke-11,[1] sedangkan pasukan mereka yang tersisa dipindahkan ke front I...

86Gambar sampul kompilasi Blu-ray pertama, menampilkan Vladilena Lena Milizé.Nama asliJepang86-エイティシックス-HepburnEiti Shikkusu Negara asalJepangJumlah episode23 + 3 SpecialRilisSaluran asliTokyo MX, BS11, GYT, GTV, ytv, CTVTanggal tayang11 April 2021 (2021-04-11) –19 Maret 2022 (2022-3-19) 86 adalah serial anime berdasarkan seri novel ringan dengan nama yang sama yang ditulis oleh Asato Asato dan diilustrasikan oleh Shirabii. Adaptasi seri diumumkan dalam siara...

South Korean singer (born 1984) This article is about the South Korean singer. For her self-titled EP, see Sandara Park (EP). The native form of this personal name is Park Sandara. This article uses Western name order when mentioning individuals. In this Korean name, the family name is Park. Sandara ParkPark in September 2022Born (1984-11-12) November 12, 1984 (age 39)Busan, South KoreaOther namesDaraOccupationsSingeractresstelevision hostAgentStar Magic (2004–2007)RelativesTh...
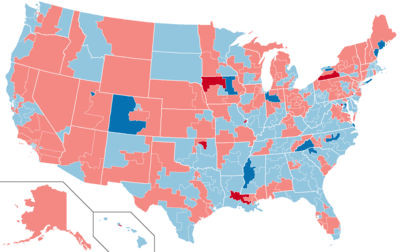
1986 United States elections← 1984 1985 1986 1987 1988 → Midterm electionsElection dayNovember 4Incumbent presidentRonald Reagan (Republican)Next Congress100thSenate electionsOverall controlDemocratic gainSeats contested35 of 100 seats (34 Class 3 seats + 1 special election)Net seat changeDemocr...

Questa voce sull'argomento film d'azione è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Fuga da SeattleJake Gyllenhaal e Jared Leto in una scena del filmTitolo originaleHighway Paese di produzioneStati Uniti d'America Anno2002 Durata97 min Genereazione RegiaJames Cox SceneggiaturaScott Rosenberg ProduttoreScott Rosenberg, Guy Riedel Produttore esecutivoMichal Gruber, Donna Langley FotografiaMauro Fior...

Bupati PaniaiPetahanaMeki Fritz Nawipasejak 23 November 2018Masa jabatan5 tahun (definitif)Dibentuk2001Pejabat pertama-Situs webpaniaikab.go.id/main/ Berikut ini adalah daftar Bupati Paniai yang menjabat sejak pembentukannya pada tahun 2001. No Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Wakil Bupati - Zubaer Husein Tidak diketahui 2007 - [Ket. 1] – 1 Naftali YogiS.Sos. 22 Februari 2007 22 Februari 2012 1 [1] Derek PakageS.IP. - Drs.F.A. Gatotkodjo 22 Februari 2012 12 ...

Pour les personnes ayant le même patronyme, voir Masson. Pierre-Maurice Masson Pierre-Maurice Masson en 1901 collection particulière Données clés Naissance 4 octobre 1879 Metz, Moselle Décès 16 avril 1916 (à 36 ans) Flirey, Meurthe-et-Moselle Nationalité Française Pays de résidence Suisse, 1904-1914 Profession Écrivain, critique. Autres activités Professeur à Fribourg Formation Normalien, agrégé, docteur (à titre posthume) Distinctions Prix d'éloquence (1906 e...

1900年美國總統選舉 ← 1896 1900年11月6日 1904 → 447張選舉人票獲勝需224張選舉人票投票率73.2%[1] ▼ 6.1 % 获提名人 威廉·麥金利 威廉·詹寧斯·布賴恩 政党 共和黨 民主党 家鄉州 俄亥俄州 內布拉斯加州 竞选搭档 西奧多·羅斯福 阿德萊·史蒂文森一世 选举人票 292 155 胜出州/省 28 17 民選得票 7,228,864 6,370,932 得票率 51.6% 45.5% 總統選舉結果地圖,紅色代表�...

Artikel ini mengenai kampung di Lampung. Untuk pengertian lain, lihat kampung Artikel ini adalah bagian dari seriPembagian administratifIndonesia Tingkat I Provinsi Daerah istimewa Daerah khusus Tingkat II Kabupaten Kota Kabupaten administrasi Kota administrasi Tingkat III Kecamatan Distrik Kapanewon Kemantren Tingkat IV Kelurahan Desa Dusun (Bungo) Finua Gampong Kute Kalurahan Kampung Kalimantan Timur Lampung Papua Riau Lembang Nagari Nagori Negeri Maluku Maluku Tengah Negeri administratif O...

Indian painter and writer (1871–1951) Not to be confused with Rabindranath Tagore. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Abanindranath Tagore – news · newspapers · books · scholar · JSTOR (May 2015) (Learn how and when to remove this message) শিল্পাচার্য - Great Teacher of t...

Ogun's delegation in Nigeria's National Assembly Politics of Nigeria Constitution Human rights Government President (list) Bola Tinubu Vice President Kashim Shettima Cabinet Federal Parastatals Legislature National Assembly of Nigeria Senate President Godswill Akpabio (APC) Deputy President Barau Jibrin (APC) (List of members of the Senate) House of Representatives Speaker Abbas Tajudeen (APC) Deputy Speaker Benjamin Okezie Kalu (APC) (List of members of the House) State delegations Abia Adam...

Bandar Udara Internasional BradleyIATA: BDLICAO: KBDLFAA LID: BDL BDLLokasi Bandara Internasional BradleyInformasiJenisPublikPemilikNegara Bagian ConnecticutPengelolaConnecticut Airport AuthorityMelayaniHartford, Connecticut dan Springfield, MassachusettsLokasiWindsor Locks, Connecticut / Hartford County, ConnecticutKetinggian dpl53 mdplKoordinat41°56′20″N 72°41′0″W / 41.93889°N 72.68333°W / 41.93889; -72.68333Situs webBradleyAirport.comLandasan p...

У статті наведено список втрат українських військовослужбовців у російсько-українській війні 1 серпня — 23 серпня 2014 року. 12 серпня 2014 року — початок масованого вторгнення регулярних підрозділів Збройних сил РФ в Україну. Докладніше: Втрати силових структур внас...

World War II Allied nuclear weapons program This article is about the atomic bomb project. For other uses, see Manhattan Project (disambiguation). Manhattan DistrictThe Trinity test of the Manhattan Project on 16 July 1945 was the first detonation of a nuclear weapon.Active1942–1946Disbanded15 August 1947CountryUnited StatesUnited KingdomCanadaBranchU.S. Army Corps of EngineersGarrison/HQOak Ridge, Tennessee, U.S.Anniversaries13 August 1942EngagementsAllied invasion of ItalyAllied invasion ...

Age of Empires III: The Asian Dynasties Información generalDesarrollador Ensemble Studios y Big Huge GamesDistribuidor MicrosoftDiseñador Bruce ShelleyDatos del juegoGénero Estrategia en tiempo realModos de juego Monojugador y Multijugador (hasta 8 jugadores)Clasificaciones ESRBPEGIDatos del softwarePlataformas Windows XP-Vista - Mac OS XDatos del hardwareFormato 1 CDDispositivos de entrada teclado DesarrolloLanzamiento 23 de octubre de 2007.[1]Age of Empires Age of Empires III: The...

الهقار تي في معلومات عامة النوع منوعة المالك علي بوجمعة المدير علي قايدي تاريخ التأسيس 2012 البلد الجزائر المقر الرسمي الجزائر الموقع الرسمي الموقع الرسمي لتلفزيون الهقار عبر الساتل أتلانتك بيرد7 تردد 11603 أفقي 2750011603 أفقي 27500 تعديل مصدري - تعديل هي قناة جزائرية مستقلة ...

село Яснище Країна Україна Область Львівська Район Золочівський Громада Підкамінська селищна громада Код КАТОТТГ UA46040110330028835 Основні дані Засноване 1546 Населення 208 Площа 0,545 км² Густота населення 381,65 осіб/км² Поштовий індекс 80696[1] Телефонний код +380 3266[2] ...

Château Saint-Gilles Nom local قلعة طرابلس Début construction 1103 Propriétaire initial Raymond de Saint Gilles Coordonnées 34° 26′ 00″ nord, 35° 50′ 40″ est Pays Liban Région historique Gouvernorat du Nord Ville Tripoli Géolocalisation sur la carte : Liban Château Saint-Gilles modifier Qala'at Sanjil et Qala'at Tarablus en arabe, est une citadelle et un fort sur une colline à Tripoli, au Liban. Autrefois connue sous le nom...

Classe Implacable Le HMS Implacable. Caractéristiques techniques Type porte-avions Longueur 233,6 m Maître-bau 29,18 m Tirant d'eau 8,8 m Déplacement 23 450 long tons (23 825 t) À pleine charge 32 110 long tons (32 624 t) Propulsion Turbines à vapeur (8 chaudières Admiralty 3 tambours, 4 arbres, turbines Parsons) Puissance 148 000 ch Vitesse 32 nœuds (59 km/h) Caractéristiques militaires Blindage Coque: 114 ...

2021 studio album by MadlibSound AncestorsStudio album by MadlibReleasedJanuary 29, 2021 (2021-01-29)GenreBoom bapinstrumental hip hopLength41:15LabelMadlib InvazionProducerMadlibMadlib chronology Pardon My French(2020) Sound Ancestors(2021) In the Beginning, Vol. 1(2021) Singles from Sound Ancestors Road of the Lonely OnesReleased: December 14, 2020 HopprockReleased: January 4, 2021 DirtknockReleased: January 22, 2021 Sound Ancestors is a studio album by American music...













