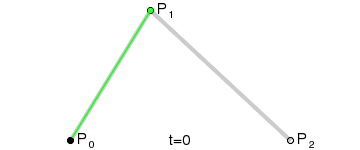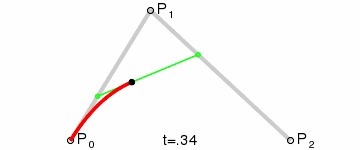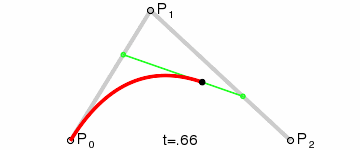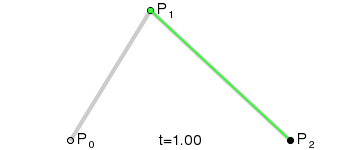
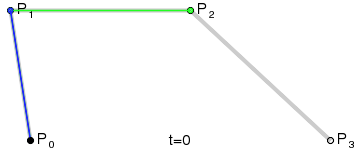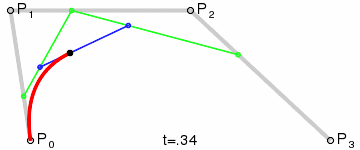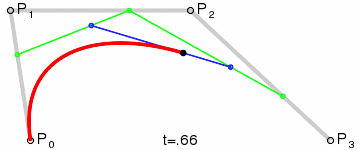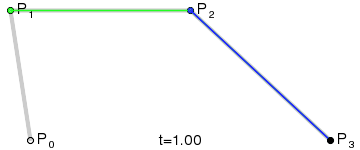
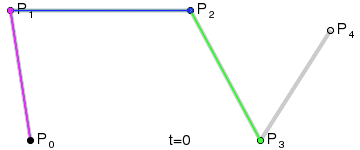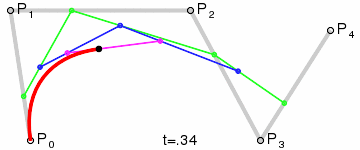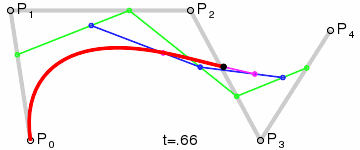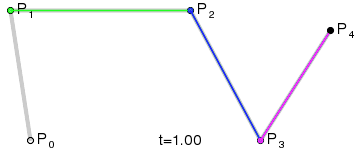
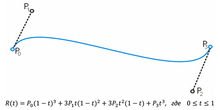
Кривая Безье
|
Read other articles:

1995 novel by Dave Stone This article is about the 1995 novel. For the topic, see sky pirate and skyjacker. For other uses, see sky pirate (disambiguation). Sky Pirates! AuthorDave StoneCover artistJeff CumminsSeriesDoctor Who book:Virgin New AdventuresRelease number40SubjectFeaturing:Seventh DoctorBernice, Chris, RozPublisherVirgin BooksPublication dateJuly 1995ISBN0-426-20446-8Preceded byOriginal Sin Followed byZamper Sky Pirates! is an original novel written by Da...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مايو 2021) الاتحاد السعودي لكرة القاعدة والكرة الناعمة الرياضة كرة القاعدة، والكرة اللي

AuriaccomuneAuriac – VedutaIl Municipio (sulla destra il Monumento ai caduti) LocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Pirenei Atlantici ArrondissementPau CantoneTerres des Luys et Coteaux du Vic-Bilh TerritorioCoordinate43°27′N 0°18′W / 43.45°N 0.3°W43.45; -0.3 (Auriac)Coordinate: 43°27′N 0°18′W / 43.45°N 0.3°W43.45; -0.3 (Auriac) Superficie5,29 km² Abitanti258[1] (2009) Densità48,77 ab...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Dezembro de 2013) Coordenadas: 38° 22' N 21° 4' E Equinadas EquinadasLocalização aproximada do centro do arquipélago das Equinadas na Grécia Coordenadas: 38° 22' N 21° 4' E Mapa do arquipélago das Equinadas Geograf...

Australian tennis player Garton HoneFull nameGarton Maxwell HoneCountry (sports) AustraliaBorn(1901-02-21)21 February 1901Morphett Vale, South AustraliaDied28 May 1991(1991-05-28) (aged 90)Myrtle Bank, South AustraliaSinglesGrand Slam singles resultsAustralian OpenSF (1924)Wimbledon1R (1939)DoublesGrand Slam doubles resultsAustralian OpenSF (1925)Wimbledon1R (1939)Mixed doublesGrand Slam mixed doubles resultsAustralian OpenF (1924)Wimbledon3R (1939) Dr. Gart...

1934 film by Henry Hathaway The Last Round-UpTheatrical release posterDirected byHenry HathawayScreenplay byRandolph ScottBased onThe Border Legionby Zane GreyProduced byHarold HurleyStarring Randolph Scott Monte Blue Barbara Fritchie CinematographyArchie StoutMusic byHerman HandProductioncompanyParamount PicturesDistributed byParamount PicturesRelease date May 1, 1934 (1934-05-01) (USA) Running time61 minutesCountryUnited StatesLanguageEnglish The Last Round-Up is a 1934 A...

Koordinat: 5°08′15″S 119°32′53″E / 5.1376003°S 119.5481758°E / -5.1376003; 119.5481758 Bonto BungaDesaKantor Desa Bonto Bunga di Dusun ManjallingNegara IndonesiaProvinsiSulawesi SelatanKabupatenMarosKecamatanMoncongloeKode pos90564[1]Kode Kemendagri73.09.13.2004 Luas10,02 km² tahun 2017Jumlah penduduk1.355 jiwa tahun 2017Kepadatan135,23 jiwa/km² tahun 2017Jumlah RT10Jumlah RW5 Bonto Bunga (Ejaan Van Ophuijsen: Bonto Boenga; Lontara Bugis &...

ستيف وودن معلومات شخصية الميلاد 6 يناير 1955 (العمر 68 سنة)بيركنهيد [لغات أخرى] الطول 1.79 م (5 قدم 10 بوصة) مركز اللعب مهاجم الجنسية نيوزيلندا المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1972–1975 Cammell Laird 1907 F.C. [الإنجليزية] 1975 ترانمير روفرز 3 (0) 1975–1976 New Brighton A.F.C.&...

Sports season1893 AHAC seasonLeagueAmateur Hockey Association of CanadaSportIce hockeyDurationJanuary 7, 1893 – March 17, 1893Number of teams51893ChampionsMontreal Hockey ClubAHAC seasons← 18921894 → Montreal Hockey Club with the Stanley Cup The 1893 Amateur Hockey Association of Canada season lasted from January 7 until March 17. The Montreal Hockey Club defeated the Crystals 2-1 to claim the league and Canadian champion for the sixth season in a row and was awarded the new S...

Not to be confused with Drama Centre London. Drama Studio LondonOther nameDSLTypeDrama schoolStudents100+LocationEaling, EnglandAffiliations Federation of Drama Schools Websitedramastudiolondon.co.uk Drama Studio London (DSL) is a British drama school in London. It is accredited by the Federation of Drama Schools.[1] The Drama Studio London was founded in 1966 by actor and director Peter Layton,[2] focusses on developing individual talent nurtured around what makes each studen...

1951 film by Arthur Pierson Home Town StoryTheatrical release posterDirected byArthur PiersonWritten byArthur PiersonProduced byArthur PiersonStarringJeffrey LynnDonald CrispMarjorie ReynoldsMarilyn MonroeAlan Hale Jr.CinematographyLucien N. AndriotEdited byWilliam F. ClaxtonMusic byLouis ForbesAlfred NewmanDistributed byMetro-Goldwyn-MayerRelease date May 18, 1951 (1951-05-18) Running time61 minutesCountryUnited StatesLanguageEnglishBox office$334,000[1] Home Town Stor...

Telaga AngkerSutradara Sisworo Gautama Putra Produser Ram Soraya Ditulis oleh Naryono Prayitno PemeranSuzzanna George Rudy Sendy Taroreh Rukman Herman Nina AnwarDistributorSoraya Intercine FilmsTanggal rilis1984Durasi115 menitNegara Indonesia Bahasa Indonesia Telaga Angker adalah film horror Indonesia yang dirilis pada tahun 1984 dengan disutradarai oleh Sisworo Gautama Putra dan dibintangi antara oleh Suzzanna, George Rudy, Sendy Taroreh, Rukman Herman, dan Nina Anwar. Sinopsis Anita (Suzann...

Town in County Wexford, Ireland This article is about the town in Ireland. For other uses, see Gorey (disambiguation). Town in Leinster, IrelandGorey GuaireTownMain Street Coat of armsGoreyLocation in IrelandCoordinates: 52°40′37″N 6°17′31″W / 52.677°N 6.292°W / 52.677; -6.292CountryIrelandProvinceLeinsterCountyCounty WexfordElevation48 m (157 ft)Population (2022)[1]11,517Time zoneUTC±0 (WET) • Summer (DST)UTC+1 (IST)Eirc...

See also: Ślesin, Kuyavian-Pomeranian Voivodeship Place in Greater Poland Voivodeship, PolandŚlesinHoly Family Monument, landmark to commemorate the independence of Poland Coat of armsŚlesinCoordinates: 52°22′N 18°18′E / 52.367°N 18.300°E / 52.367; 18.300Country PolandVoivodeshipGreater PolandCountyKoninGminaŚlesinFirst mentioned1231Town rights1358Area • Total7.18 km2 (2.77 sq mi)Population (2006) • Total3,10...

Untuk prekuelnya, lihat London Love Story. London Love Story 2Sutradara Asep Kusdinar Produser Sukhdev Singh Wicky V. Olindo Ditulis oleh Sukhdev Singh Tisa TS SkenarioSukhdev SinghTisa TSCeritaTisa TSPemeran Michelle Ziudith Dimas Anggara Rizky Nazar Salshabilla Adriani Mawar Eva de Jongh Ramzi Ina Marika Irene Librawati Penata musikJoseph S. DjafarSinematograferRama HermawanPenyuntingWawan I. WibowoPerusahaanproduksiScreenplay FilmsDistributor Screenplay Films Disney+ Hotstar Netflix ...

Australian equestrian Sharon Jarvis2016 Australian Paralympic team portraitPersonal informationBorn (1978-10-31) 31 October 1978 (age 45)SportCountryAustraliaSportPara-equestrian Medal record Equestrian World Equestrian Games 2010 Kentucky Individual Test Grade III 2010 Kentucky Freestyle Test Grade III Sharon Jarvis (born 31 October 1978) is an Australian para-equestrian. She represented Australia at the three Summer Paralympics - 2008 Beijing, 2016 Rio and 2020 Tokyo .[1] Perso...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Yasumichi UchimaInformasi pribadiNama lengkap Yasumichi UchimaTanggal lahir 10 September 1984 (umur 39)Tempat lahir Prefektur Okinawa, JepangPosisi bermain BekKarier senior*Tahun Tim Tampil (Gol)2007-2009 Sagan Tosu 2010-2012 Gainare Tottori * Pe...

В Википедии есть статьи о других людях с фамилией Тейлор. Джозеф Хотон Тейлорангл. Joseph Hooton Taylor Дата рождения 29 марта 1941(1941-03-29)[1][2] (82 года) Место рождения Филадельфия, США Страна США Научная сфера физика Место работы Массачусетский университет в Амхерсте[d] Ал...

Chemical compound BenorilateClinical dataRoutes ofadministrationOralATC codeN02BA10 (WHO) Identifiers IUPAC name 4-acetamidophenyl 2-(acetyloxy)benzoate CAS Number5003-48-5 NPubChem CID21102ChemSpider19846 NUNIIW1QX9DV96GChEMBLChEMBL162036 NCompTox Dashboard (EPA)DTXSID5022649 ECHA InfoCard100.023.340 Chemical and physical dataFormulaC17H15NO5Molar mass313.309 g·mol−13D model (JSmol)Interactive image SMILES O=C(C)Oc2ccccc2C(=O)Oc1ccc(NC(C)=O)cc1 InChI InChI=1S...

Legendary sumo wrestler Nomi no Sukune by Kikuchi Yōsai Nomi no Sukune (野見 宿禰) was a legendary figure in Japanese history, regarded as the founder of sumo wrestling.[1] He was the founder of the Haji no Muraji clan.[2] Life Nomi no Sukune wrestling with Taima no Kehaya (by Yoshitoshi) Sukune is said to have lived during the reign of Emperor Suinin (29 BC – 70).[3] Allegedly, in 23 B.C., the Emperor instructed Nomi no Sukune to deal with Taima no Kehaya (当�...






























![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)








![{\displaystyle \mathbf {B} (t)=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}\quad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/184d535909668636476113a80ef52c158fb23e31)
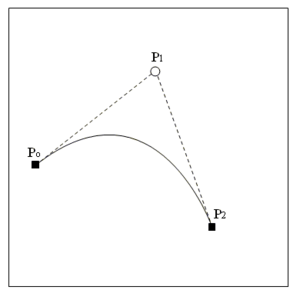
![{\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2t(1-t)\mathbf {P} _{1}+t^{2}\mathbf {P} _{2},\quad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39003f739f43fd3080ea11c28f4dba23944e9ac)




![{\displaystyle \mathbf {B} (t)=(1-t)^{3}\mathbf {P} _{0}+3t(1-t)^{2}\mathbf {P} _{1}+3t^{2}(1-t)\mathbf {P} _{2}+t^{3}\mathbf {P} _{3},\quad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26ff769812d3f7ad991b184a4ff63bfd08fd2919)