仮説検定
|
Read other articles:

Mangrove ecoregion in Central America Mosquitia-Nicaraguan Caribbean Coast mangrovesBig Corn Island, 70 km east of Nicaragua coastEcologyBiomeMangrovesGeographyArea4,400 km2 (1,700 sq mi)CountriesHondurasNicaraguaConservationConservation statusRelatively Stable/Intact[1] The Mosquitia-Nicaraguan Caribbean Coast mangroves ecoregion, in the Mangrove biome, are along the Caribbean coasts of Nicaragua and Honduras as well as off shore islands such as the Corn Islands. Descr...

Agencia Espacial del Perú - CONIDALocalizaciónPaís Perú PerúInformación generalSigla CONIDATipo organismo públicoSede Luis Felipe Villarán 1069, San Isidro, LimaOrganizaciónJefe Institucional MAG FAP José Antonio García MorganDepende de Ministerio de DefensaHistoriaFundación 11 de junio de 1974Sitio web oficial[editar datos en Wikidata] La Comisión Nacional de Investigación y Desarrollo Aeroespacial (CONIDA) es el organismo que rige las actividades relacionadas co...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mikkeli Province – news · newspapers · books · scholar · JSTOR (October 2021) (Learn how and when to remove this template message) Mikkeli ProvinceMikkelin lääniS:t Michels länProvince of Finland1831–1997 Coat of arms CapitalMikkeliArea • 1.1.199321,628 km2...

Gereja di Novorossisk Eparki Novorossisk adalah sebuah eparki Gereja Ortodoks Rusia yang terletak di Novorossisk, Federasi Rusia. Eparki tersebut didirikan pada tahun 1919.[1] Referensi ^ http://www.patriarchia.ru/db/text/2844968.html lbsKeuskupan Gereja Ortodoks RusiaPatriark MoskwaEparki di Rusia Abakan dan Khakassia Akhtubinsk Alapayevsk Alatyr Alexdanrov Almetyevsk Amur Anadyr Ardatov Arkhangelsk Armavir Arsenyev Astrakhan Balashov Barnaul Barysh Belgorod Belyov Bezhetsk Birobidzh...

العلاقات العراقية البالاوية العراق بالاو العراق بالاو تعديل مصدري - تعديل العلاقات العراقية البالاوية هي العلاقات الثنائية التي تجمع بين العراق وبالاو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة العر�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Gambar tumor sel Sertoli-Leydig di bawah mikroskop Arenoblastoma adalah jenis kanker ovarium yang langka dan termasuk golongan tumor sel Sertoli-Leydig.[1][2][3] Dari seluruh kasus kanker ovarium, hanya kurang dari 0,5% yang me...

Tallo Gadji oleh Ben Sutherland, 2015Informasi pribadiNama lengkap Tallo Carmel Gadji-Celi Jr.Tanggal lahir 21 Desember 1992 (umur 31)Tempat lahir Magbehigouepa,[1] Pantai GadingTinggi 1,87 m (6 ft 1+1⁄2 in)Posisi bermain PenyerangInformasi klubKlub saat ini SC Bastia (pinjaman dari Roma)Nomor 11Karier junior2005–2006 Stella Club d'Adjamé2007–2008 Centre de formation Cyril Domoraud[2]2010–2011 Chievo2011 → Internazionale (pinjaman)Karier sen...

Dalam artikel ini, nama keluarganya adalah Zhang. Zhang YugeZhang, 2019Lahir11 Mei 1996 (umur 27)Harbin, Heilongjiang, TiongkokNama lainTakoPekerjaanPenyanyipenariaktrisTahun aktif2013–sekarangKarier musikGenrePopMandopopK-popJ-popInstrumenVokalLabelStar48Ninestyle Model AgencyNinestyle MusicArtis terkaitSNH48Style-77Senses Zhang Yuge Nama Tionghoa Hanzi tradisional: 張語格 Hanzi sederhana: 张语格 Alih aksara Mandarin - Hanyu Pinyin: Zhāng Yǔgé Nama Korea Hangul: 장...

Hungarian Space Research OfficeAgency overviewFormedJanuary 1992 (1992-01)JurisdictionGovernment of HungaryHeadquartersBudapest, HungaryAgency executiveDr. Fruzsina Tari, DirectorWebsitehso.hu The Hungarian Space Research Office (HSO; Hungarian: Magyar Űrkutatási Iroda) is the official Government of Hungary agency responsible for the civilian space program as well as aeronautics and aerospace research. It is the organization whose purpose is to coordinate Hungarian space explorati...
Artikel ini adalah bagian dari seri:Permainan video Pelantar Dingdong Konsol permainan Konsol video rumah Permainan elektronik Konsol genggam Permainan ponsel Permainan daring Permainan PC Linux Mac Genre Laga Berhantam Bertarung Arung pelantar Bertahan hidup Siluman Bertahan hidup horor Petualangan Bermain peran Bermain peran laga Bermain peran taktik Simulasi Konstruksi dan manajemen Simulasi kehidupan Olahraga Kendaraan Strategi Bertarung daring banyak pemain Strategi waktu nyata Taktik wa...

Former American mobile network provider payLo redirects here. For the actress, see Paydin LoPachin. Virgin Mobile USACompany typeSubsidiaryIndustryWireless communicationsEntertainmentFoundedOctober 18, 2001; 22 years ago (2001-10-18)San Francisco, California, United StatesFounderRichard BransonJohn Tantum[dubious – discuss]DefunctJanuary 2020; 4 years ago (2020-01)FateMerged with Boost Mobile on February 2, 2020 (2020-...

Xiamafang下马坊Nama lainMonumen Sun Yat-sen (中山陵)LokasiDistrik Xuanwu, Nanjing, JiangsuChinaOperatorNanjing Metro Co. Ltd.Jalur Jalur 2KonstruksiJenis strukturBawah tanahSejarahDibuka28 Mei 2010Operasi layanan Stasiun sebelumnya Nanjing Metro Stasiun berikutnya Muxuyuan Yuzui Jalur 2Xiaolingwei Jingtianlu Sunting kotak info • L • BBantuan penggunaan templat ini Stasiun Xiamafang (Stasiun Monumen Sun Yat-sen, Hanzi: 下马坊站)...

Франц Саксен-Кобург-Заальфельдскийнем. Franz von Sachsen-Coburg-Saalfeld герцог Саксен-Кобург-Заальфельдский 8 сентября 1800 — 9 декабря 1806 Предшественник Эрнст Фридрих Саксен-Кобург-Заальфельдский Преемник Эрнст I Саксен-Кобург-Заальфельдский Рождение 15 июля 1750(1750-07-15)Кобург, Сакс...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

County in New York, United States For other uses, see Wayne County. Not to be confused with Wayne, New York or Wayne County, Michigan. County in New YorkWayne CountyCountyWayne County Courthouse in Lyons FlagSealLocation within the U.S. state of New YorkNew York's location within the U.S.Coordinates: 43°17′N 77°03′W / 43.28°N 77.05°W / 43.28; -77.05Country United StatesState New YorkFounded1823Named forAnthony WayneSeatLyonsLargest townArcadiaGovernme...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2020) الأسماء النائبة أو أسماء الحيز هي كلمات يمكنها الإشارة إلى ما لم يكن له اسم بعد، أو إلى ما كان اسمه منسيًا...
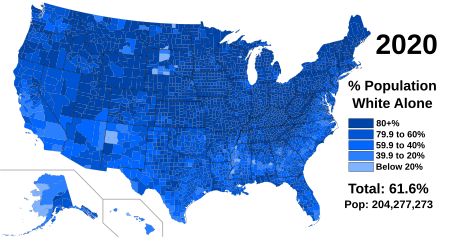
Kulit putih Amerika SerikatKulit putih Amerika Serikat (murni/satu ras saja) pada tahun 2020Jumlah populasi235.411.507 (71,02%) Kulit putih murni atau campuran 204.277.273 (61,63%) Kulit putih murni 31.134.234 (9,39%) Kulit putih campuran [1]Daerah dengan populasi signifikanSemua wilayah di Amerika SerikatBahasaMayoritas Bahasa InggrisAgamaProtestan 48%Katolik 19%Mormon 2%Yahudi 3%Lainnya 3%Tidak beragama 24%[2] Kulit putih Amerika Serikat (juga disebut sebagai Eropa Amerika S...

تعداد إيران 2016 المعلومات البلد إيران الموقع إيران التاريخ 2016 تعديل مصدري - تعديل طبقا للمركز الإحصائي في إيران في عام 2016 وصل عدد السكان بايران إلى 79,926,270 مليون نسمة حيث 39,427,828 اناث و40,498,442 ذكور.[1] وتظهر الدراسات ان معدل النمو السكاني سيستمر بالتباطؤ حتى يستق...

Questa voce sull'argomento cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. George McCloudGeorge McCloud nel 2002Nazionalità Stati Uniti Altezza198 cm Peso93 kg Pallacanestro RuoloAla piccola Termine carriera2002 CarrieraGiovanili Mainland High School1985-1989 Fl. State Seminoles117 (1.577) Squadre di club 1989-1993 Indiana Pacers247 (1.358)1993-1994 V.L. Pesar...

جويل روبلز (بالإسبانية: Joel Robles) معلومات شخصية الاسم الكامل جويل روبلز بلازكيز الميلاد 17 يونيو 1990 (العمر 34 سنة)خيتافي ، إسبانيا الطول 1.95 م (6 قدم 5 بوصة) مركز اللعب حارس مرمى الجنسية إسباني معلومات النادي النادي الحالي ليدز يونايتد الرقم 22 مسيرة الشباب سنوات فريق 2...

