十分統計量
|
Read other articles:

Gempa bumi Hokkaidō 2003 平成15年(2003年)十勝沖地震Kebakaran di TomakomaiKushiro Map showing the epicenter of the mainshockTampilkan peta HokkaidoGempa bumi Hokkaido 2003 (Jepang)Tampilkan peta JepangWaktu UTC2003-09-25 19:50:06ISC7134409USGS-ANSSComCatTanggal setempat26 September 2003Waktu setempat04:50Kekuatan8.3 Mw[1]Kedalaman27 km (17 mi)Episentrum41°47′N 143°52′E / 41.78°N 143.86°E / 41.78; 143.86Koordinat: 41°47′N 1...

Locality in Aragon, SpainLardiésLocalityLardiésShow map of AragonLardiésShow map of SpainCoordinates: 42°29′55″N 0°7′58″W / 42.49861°N 0.13278°W / 42.49861; -0.13278[1]Country SpainAutonomous community AragonProvinceProvince of HuescaMunicipalityFiscal, AragonElevation907 m (2,976 ft)Population • Total10 Lardiés is a hamlet located in the municipality of Fiscal, Aragon, in Huesca province, Aragon, Spain. As of 202...

South Korean general and martial artist (1918–2002) This article cites its sources but does not provide page references. You can help providing page numbers for existing citations. (March 2024) (Learn how and when to remove this template message) In this Korean name, the family name is Choi. Choi Hong-hiBorn(1918-11-09)9 November 1918Hwadae, Myongchon County, Kankyōhoku-dō (North Hamgyong Province), Korea, Empire of JapanDied15 June 2002(2002-06-15) (aged 83)Pyongyang, North KoreaSty...

James Madison ParkGarden on the James Madison shelter roof, c. 2014LocationMadison, WisconsinCoordinates43°04′53″N 89°22′59″W / 43.08126°N 89.38319°W / 43.08126; -89.38319Area12.63-acre (51,100 m2)Operated byCity of MadisonPublic transit access Metro Transit James Madison Park is a 12.63-acre (51,100 m2) waterfront park located on Lake Mendota in Madison, Wisconsin. It is owned by the city of Madison.[1] Gates of Heaven Synagogue The ...

Pour les articles homonymes, voir Braine. Cet article est une ébauche concernant une localité brabançonne wallonne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Braine-le-Château Le château des comtes de Hornes ou château de Robiano (XIIe siècle). Héraldique Drapeau Administration Pays Belgique Région Région wallonne Communauté Communauté française Province Province du Brab...

Vous lisez un « bon article » labellisé en 2015. Pour les articles homonymes, voir GO. Grand Orient de FranceHistoireFondation 1773CadreSigle InstitutionelementZone d'activité Europe, Amérique, Asie, Océanie, AfriqueType Obédience maçonniqueForme juridique Association loi de 1901Siège Hôtel du Grand Orient de France (16, rue Cadet, 75009, Paris)Pays FranceOrganisationFondateur Anne Charles Sigismond de Montmorency-LuxembourgGrand maître Guillaume Trichard (d) (depu...

German publishing house Manesse VerlagParent companyPenguin Random HouseFounded1944Country of originGermanyHeadquarters locationMunichKey peopleHorst LauingerFiction genresClassic LiteratureOfficial websitewww.manesse.ch The Manesse Verlag is a German publishing house for classical literature, founded in 1944 in Zürich in Switzerland. It belongs today to Random House publishing group based in Munich. The publishing house is mainly known for its library of world literature.[1] It also...

Scheduling algorithm, the first piece of data inserted into a queue is processed first This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: FIFO computing and electronics – news · newspapers · books · scholar · JSTOR (March 2015) (Learn how and when to remove this message) Representation of a FIFO queue In c...

Pub in Whitehall, London The Old ShadesThe Old ShadesThe Old ShadesShow map of City of WestminsterThe Old ShadesShow map of Greater LondonGeneral informationAddress37–39 WhitehallTown or cityLondonCountryEnglandCoordinates51°30′23″N 0°07′37″W / 51.506486°N 0.12691162°W / 51.506486; -0.12691162Opened1898Design and constructionArchitecture firmTreadwell and MartinDesignations Listed Building – Grade IIOfficial nameOld Shades Public HouseDesignated5 Februa...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (décembre 2020). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ?...

Indonesian spicy water spinach dish Plecing kangkungPlecing kangkungPlace of originIndonesiaRegion or stateBali and LombokServing temperatureCold and freshMain ingredientsKangkung and plecing sambal Media: Plecing kangkung Plecing kangkung is an Indonesian spicy water spinach dish from the island of Bali and Lombok. Plecing kangkung is made from blanched water spinach leaves (Ipomoea aquatica) and served cold with plecing sambal made from ground red chili pepper, shallot, garlic, bi...

Remaining life expectancy is the expected remaining number of years of life as a function of current age.[1] Life expectancy at birth is indicated above the 0 current age. Life expectancy in the US states in 2019[2] Life expectancy in the US states in 2020[3] Alernative visualization of data for 2020[3] Development of life expectancy in the US according to estimation of the World Bank Group[4] Life expectancy with calculated gender gap[4] Life ...

مجموعة من العصي المتألقة العصا المضيئة مصدر ضوئي مكثف ذاتياً وقصير الأمد، وهو يتألف من أنبوب بلاستيكي شفاف يحتوي على مواد عازلة، تصدر الضوء بعميلة توهج كيميائي، لذلك لا تتطلب العملية مصدر طاقة خارجي.[1][2] لا يمكن إيقاف الضوء ويمكن استخدامها مرة واحدة فقط. وغالبا ما ...

You can help expand this article with text translated from the corresponding article in Polish. (December 2021) Click [show] for important translation instructions. View a machine-translated version of the Polish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikip...

Differentiation under the integral sign formula This article is about the integral rule. For the convergence test for alternating series, see Alternating series test. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Leibniz integral rule – news · newspapers · books · scholar · JSTOR (October 2016) (Learn how ...

Soviet military official and diplomat Ivan Ilyichev Ivan Ivanovich Ilyichev (Russian: Иван Иванович Ильичёв; 14 August 1905 – 2 September 1983) was a Soviet military official and diplomat.[1] Born in Navoloki, Kaluga Governorate in 1905, Ilyichev joined the Russian Communist Party (bolsheviks) in 1925 and went on to serve in the Red Army. He studied at the Lenin Military-Political Academy until May 1938, and after graduation he became the head of the Political...

Impatiens edgeworthii Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Asterid Ordo: Ericales Famili: Balsaminaceae Genus: Impatiens Spesies: Impatiens edgeworthii Nama binomial Impatiens edgeworthiiHook.f. Impatiens edgeworthii adalah spesies tumbuhan yang tergolong ke dalam famili Balsaminaceae. Spesies ini juga merupakan bagian dari ordo Ericales. Spesies Impatiens edgeworthii sendiri merupakan bagian ...
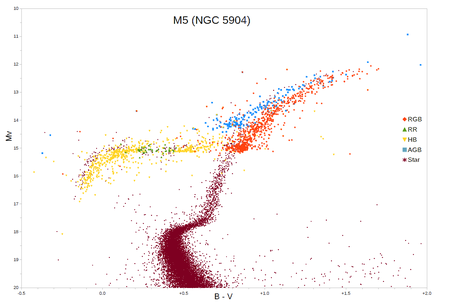
النجوم الشبيهة بالشمس لها قلب متحلل على فرع العمالقة الحمر حيث يصعد إلى الحافة (الرأس) قبل بدء اندماج الهيليوم الأساسي مع اشعاع وميض شديد. رأس فرع العملاق الأحمر (TRGB) هو مؤشر المسافة الأساسي المستخدم في علم الفلك. يستخدم هذا المؤشر ضياء أكثر نجوم فرع العملاق الأحمر سطوعًا في...

Artikel ini merupakan bagian dari ProyekWiki berikut ini: ProyekWiki Geografi (Dinilai kelas templat, Mid) GeografiWikipedia:ProyekWiki GeografiTemplat:ProyekWiki GeografiArtikel Geografi Portal Geografi lbsTemplat ini berada dalam lingkup ProyekWiki Geografi, sebuah kolaborasi untuk meningkatkan kualitas Geografi di Wikipedia. Jika Anda ingin berpartisipasi, silakan kunjungi halaman proyek, dan Anda dapat berdiskusi dan melihat tugas yang tersedia. Templat Templat in...

Tupai ramping Tupaia gracilis Status konservasiRisiko rendahIUCN41495 TaksonomiFilumChordataKelasMammaliaOrdoScandentiaFamiliTupaiidaeGenusTupaiaSpesiesTupaia gracilis Thomas, 1893 DistribusiPeta sebaran spesies Tupai ramping (Tupaia gracilis) adalah sebuah spesies tupai dari famili Tupaiidae.[3] Tupai ini berasal dari Kalimantan dan hidup di hutan tua dataran rendah. Referensi ^ Han, K. H.; Stuebing, R. (2016). Tupaia gracilis: e.T41495A115189017. Parameter |name-list-styl...

















