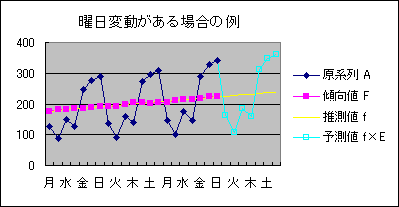
対移動平均比率法
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Roti lapis keju dan acarNama lainCheese and pickle sandwich, Cheese and chutney sandwich (dengan chutney)Tempat asalInggris RayaBahan utamaRoti, keju (jenis yang biasa dipakai Cheddar), acar (merek Branston)Sunting kotak info • L • BBantuan penggunaan templat ini Roti lapis keju dan acar (bahasa Inggris: cheese and pickle sandwich), atau terkadang disebut juga roti lapis keju dan chutney (bahasa Inggris: cheese and chutney sandwich) atau ploughman's sandwich, adalah roti lapis k...

Untuk tempat lain yang bernama sama, lihat Kendal (disambiguasi). KendalKecamatanNegara IndonesiaProvinsiJawa TimurKabupatenNgawiPemerintahan • CamatSofwan AhmadiLuas[1] • Total87,33 km2 (33,72 sq mi)Populasi • Total52.418[1] jiwa • Kepadatan600/km2 (2,000/sq mi)Kode area telepon+62 351Kode Kemendagri35.21.04 Desa/kelurahan10 Desa 48 DusunSitus webkendal.ngawikab.go.id Kendal[2] (Jawa: ꦏꦺ�...

Untuk versi televisi 2015, lihat The Dresser (film 2015). The DresserSutradaraPeter YatesProduserPeter YatesDitulis olehRonald HarwoodPemeran Albert Finney Tom Courtenay Edward Fox Zena Walker Eileen Atkins Michael Gough Cathryn Harrison Penata musikJames HornerSinematograferKelvin PikePenyuntingRay LovejoyDistributorColumbia PicturesTanggal rilis 9 Desember 1983 (1983-12-09) Durasi118 menitNegaraBritania RayaBahasaInggrisPendapatankotor$5,310,748 The Dresser adalah sebuah film 198...

American SplendorPoster film American SplendorSutradaraShari Springer BermanRobert PulciniProduserTed HopeChristine Kunewa WalkerJulia KingDeclan BaldwinDitulis olehShari Springer BermanRobert PulciniBerdasarkanAmerican Splendor dan Our Cancer Yearoleh Harvey Pekar dan Joyce BrabnerPemeranPaul GiamattiHope DavisPenata musikMark SuozzoSinematograferTerry StaceyPenyuntingRobert PulciniPerusahaanproduksiGood MachineDark Horse EntertainmentDistributorFine Line FeaturesHBO FilmsTanggal rilis...

Bandiera del Bunyoro In rosso: l'attuale regno di Bunyoro in Uganda Bunyoro chiamato anche Bunyoro-Kitara, è uno degli antichi regni dell'Africa orientale. I regni sono stati aboliti nel 1967, nel 1993 il presidente Yoweri Museveni li ha nuovamente riconosciuti come entità culturali, da quell'anno è ritornato in vigore il titolo di sovrano (Omukama); l'attuale sovrano è Solomon Gafabusa Iguru I, 27º Omukama (re) di Bunyoro-Kitara. Il territorio del regno è situato a nord-ovest del regno...

Italia Uniformi di gara Casa Trasferta Sport Pallavolo Federazione FIPAV Confederazione CEV Codice CIO ITA Selezionatore Gaetano Gagliardi(Under-20) Michele Fanni(Under-18) Pasquale D'Aniello(Under-17) Le selezioni giovanili della nazionale di pallavolo femminile dell'Italia sono gestite dalla Federazione Italiana Pallavolo (FIPAV) e partecipano ai tornei pallavolistici internazionali per squadre nazionali femminili limitatamente a specifiche classi d'età. Indice 1 Under-23 2 Under-22 3 Und...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Same-sex marriage in Canada BC AB SK MB ON QC NB PE NS NL YT NT NU Legal Reference Re Same-Sex MarriageHalpern v Canada (AG)Civil Marriage Act Parliament 38th House · 39th House Same-sex marriage by province Related Civil unions in QuebecAdult interdependent relationship in AlbertaDomestic partnership in Nova ScotiaCommon-law relationships in Manitoba vte Part of the LGBT rights seriesLegal status ofsame-sex unions Marriage Andorra Argentina Australia Austria Belgium Brazil Cana...

Fictional character in Capcom's Mega Man X series Fictional character XMega Man characterConcept art of X as seen in Maverick Hunter X by Tatsuya YoshikawaFirst appearanceMega Man X (1993)Last appearanceMega Man X Dive (2020)Created byKeiji InafuneHayato KajiVoiced by English Ruth Shiraishi (X4)Peter von Gomm (X7)Mark Gatha (2004–2006)Iain Gibb (Mega Man ZX Advent)Zach LeBlanc (Puzzle Fighter)Ted Sroka (2017–present) Japanese Megumi Ogata (X1)[1]Kentaro Ito (X4)Showtaro Morikubo (...

Criminal organization in Italy For the 1972 film originally titled Camorra, see Gang War in Naples. For the 1986 Italian film, see Camorra (1986 film). Criminal organization CamorraFounding locationCampania, ItalyYears activeSince the 17th centuryTerritoryTerritories with established coordination structures with significant territorial control are in Campania, in particular in the provinces of Naples, Caserta and Salerno. The Camorra has secondary ramifications in other Italian regi...

Dieser Artikel behandelt den Staat. Zu weiteren Bedeutungen siehe Schweiz (Begriffsklärung). Schweizerische Eidgenossenschaft Confédération suisse (französisch)Confederazione Svizzera (italienisch)Confederaziun svizra (rätoromanisch)Confoederatio Helvetica (CH) (lateinisch) Fahne Wappen Wahlspruch: “Unus pro omnibus, omnes pro uno”[1]Lateinisch für:«Einer für alle, alle für einen» (deutsch)«Un pour tous, tous pour un» (französisch)«Uno per tutti, tutti per uno» (it...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. PriscillaSutradaraSofia CoppolaProduser Sofia Coppola Youree Henley Lorenzo Mieli SkenarioSofia CoppolaBerdasarkanElvis and Meoleh Priscilla PresleySandra HarmonPemeran Cailee Spaeny Jacob Elordi SinematograferPhilippe Le SourdPenyuntingSarah FlackPerusa...

HMS Queen Elizabeth di Lemnos pada 24 April 1915 Tentang kelas Nama:Kelas Queen ElizabethOperator: Angkatan Laut Britania RayaDidahului oleh:Kapal tempur kelas-Iron DukeDigantikan oleh:Kapal tempur kelas-RevengeBertugas:1914–1947Rencana:6Selesai:5Batal:1Hilang:1 Ciri-ciri umum Kelas dan jenis Kapal tempurBerat benaman 27.500 ton (standard) 36.500 ton (muat penuh)Panjang 645 ft 9 in (196,82 m)Lebar 90 ft 6 in (27,58 m)Daya muat 30 ft 2 in (9...

United States Navy base in Virginia For US naval vessels named Yorktown, see USS Yorktown. Naval Weapons Station YorktownYorktown, Virginia Typenaval baseSite informationControlled byUnited States NavySite historyBuilt1918,In use1918–present Naval Weapons Station Yorktown is a United States Navy base in York County, James City County, and Newport News in the Hampton Roads region of Virginia. It provided a weapons and ammunition storage and loading facility for ships of the United ...

Alexander Petrovich KazhdanLahir(1922-09-03)3 September 1922Moskwa, Uni SovietMeninggal29 Mei 1997(1997-05-29) (umur 74)Washington, D.C.AlmamaterUniversitas MoskwaDikenal atasOxford Dictionary of ByzantiumKarier ilmiahBidangIlmu BizantiumInstitusiAkademi Ilmu Pengetahuan Soviet Dumbarton OaksTerinspirasiEvgenii A. Kosminskii Alexander Petrovich Kazhdan (bahasa Rusia: Алекса́ндр Петро́вич Кажда́н; 3 September 1922 – 29 Mei 1997) adalah seorang peneliti Biz...

Largest religious Zionist youth movement in the world World Bnei Akivaבני עקיבא העולמיתWorld Bnei Akiva logoBnei Akiva building in Ramat GanFormationMay 28, 1929; 95 years ago (May 28, 1929)TypeJewish Youth MovementLegal statusNon-profit organizationPurposeEducationalHeadquartersJerusalem, IsraelLocation54 King George Street, Jerusalem, IsraelCoordinates31°46.892′N 35°12.988′E / 31.781533°N 35.216467°E / 31.781533; 35.216467Region se...

Prime Minister of Denmark (1877–1962) Erik Scavenius12th Prime Minister of DenmarkIn office9 November 1942 – 29 August 1943MonarchChristian XPreceded byVilhelm BuhlSucceeded byGerman military rule(next Prime Minister: Vilhelm Buhl)Minister of Foreign AffairsIn office8 July 1940 – 29 August 1943Prime MinisterThorvald Stauning Vilhelm Buhl HimselfPreceded byPeter R. MunchSucceeded byGerman military rule(next Foreign Minister: John C. Møller)In office24 June 1913 �...

Eugenio Gaggiotti, protagonista della vicenda Il caso Gaggiotti, anche riportato come scandalo Gaggiotti,[1] fu il fallito tentativo di corruzione della partita di Serie B Fanfulla-Alessandria (1-2) del 6 dicembre 1953, per il quale la società lodigiana, in quanto responsabile dell'illecito, fu penalizzata di cinque punti nello stesso campionato. Indice 1 I fatti 2 L'inchiesta 3 Sentenze 4 Note I fatti Venerdì 4 dicembre 1953[2] Emanuele Dalla Fontana, portiere dell'Alessand...

画像提供依頼:大阪いばらきキャンパス新棟(H棟)の画像提供をお願いします。(2024年4月) 立命館大学 衣笠キャンパス大学設置 1922年創立 1900年創立者 中川小十郎学校種別 私立設置者 学校法人立命館本部所在地 京都府京都市中京区西ノ京朱雀町1キャンパス 朱雀(京都府京都市中京区)衣笠(京都府京都市北区)びわこ・くさつ(滋賀県草津市)大阪いばらき(大�...