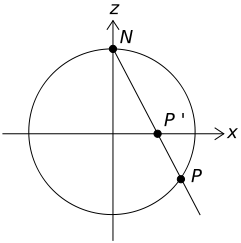
Geometria birazionale
|
Read other articles:

Darjah Kebesaran Sultan Ahmad Shah PahangDianugerahkan oleh Sultan PahangTipeOrdeDidirikan24 Oktober 1977StatusMasih dianugerahkanPendiriSultan Haji Ahmad Shah Al-Musta’in BillahPenguasaAl-Sultan Abdullah Ri'ayatuddin Al-Mustafa Billah ShahTingkatSri Sultan (S.S.A.P.) Darjah Sri Sultan (D.S.A.P.) Setia (S.A.P.) Ahli (A.A.P.)PrioritasTingkat lebih tinggiDarjah Sri Diraja Sultan Ahmad Shah PahangTingkat lebih rendahDarjah Kebesaran Mahkota PahangDarjah Kebesaran Sultan Ahmad Shah Pahang Yang ...

Disambiguazione – Se stai cercando altre forme di governo nella storia della Birmania/Myanmar, vedi Unione Birmana. Disambiguazione – Myanmar rimanda qui. Se stai cercando l'omonimo blocco Unicode, vedi Myanmar (Unicode). Disambiguazione – Burma rimanda qui. Se stai cercando altri significati, vedi Burma (disambigua). Questa voce o sezione tratta di eventi in corso o di immediata attualità. Le informazioni possono pertanto cambiare rapidamente con il progredire degli e...

Pulau Grand Bé, dilihat dari tembok Saint-Malo Grand Bé merupakan sebuah pulau gelombang di dekat Saint-Malo, Prancis. Terletak di mulut Sungai Rance, beberapa ratus meter dari tembok Saint-Malo. Ketika gelombang surut pulau dapat dicapai dengan berjalan kaki dari pantai Bon-Secours. Di pulau itu terdapat sisa-sisa benteng masa lampau. François-René de Chateaubriand, seorang penulis Prancis dari Saint-Malo, dimakamkan di pulau itu, pada sebuah makam yang menghadap ke laut. Lihat pula Peti...

سفارة اليمن في بولندا اليمن بولندا الإحداثيات 52°10′28″N 21°04′26″E / 52.174563888889°N 21.073902777778°E / 52.174563888889; 21.073902777778 البلد بولندا المكان وارسو الاختصاص بولندا الموقع الالكتروني الموقع الرسمي تعديل مصدري - تعديل سفارة اليمن في بولندا هي أرفع تمثيل دبلوماسي[1&...

A series of four paintings by English artist William Hogarth For series of paintings by Joseph Vernet, see Four Times of the Day (Joseph Vernet). The paintings of Four Times of the Day (clockwise from top left: Morning, Noon, Night, and Evening) Four Times of the Day is a series of four oil paintings by English artist William Hogarth. They were completed in 1736 and in 1738 were reproduced and published as a series of four engravings. They are humorous depictions of life in the streets of Lon...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Menorah Medical Center – news · newspapers · books · scholar · JSTOR (May 2019) (Learn how and when to remove this template message) Hospital in Kansas, United StatesMenorah Medical CenterHCA Midwest DivisionGeographyLocation5721 W. 119th Street, Overland Park, Kansas, United StatesOrganizationNetworkHCA M...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Place in Al-Anbar, IraqAl-Qa'im القائمAl-Qa'imCoordinates: 34°22′7.66″N 41°5′40.10″E / 34.3687944°N 41.0944722°E / 34.3687944; 41.0944722Country IraqProvinceAl-AnbarDistrictAl-Qa'imElevation175 m (574 ft)Population (2018) • Total74,100Time zoneUTC+3 (GMT+3)Postal code31003 View of al-Qa'im, 2009 Al-Qa'im (Arabic: القائم, Kurdish: قائیم ) is an Iraqi border town located nearly 400 km (248 mi) northwe...

Honor awarded to college basketball coaches Big Ten Coach of the YearAwarded forthe top men's basketball coach in the Big Ten ConferenceCountryUnited StatesHistoryFirst award1974Most recentFred Hoiberg,NebraskaMatt Painter, Purdue The Big Ten Conference Men's Basketball Coach of the Year, is an annual college basketball award presented to the top men's basketball coach in the Big Ten Conference. The winner is selected by the Big Ten media association and conference coaches. The award was firs...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2022) أريل بوريسيوك معلومات شخصية الميلاد 29 يوليو 1991 (العمر 32 سنة)بيالا بودلاسكا[1] الطول 1.78 م (5 قدم 10 بوصة) مركز اللعب وسط الجنسية بولندا معل...

Untuk sinetron religi Islam produksi Amanah Surga Productions, lihat Setulus Kasih Ibu. Kasih IbuGenre Drama Religi PembuatSinemArtSutradaraMaruli AraPemeran Meriam Bellina Bobby Joseph Paula Tobing Billy Davidson Ketrin Agustine Joy Octaviano Jessica Lontoh Penggubah lagu temaNikitaLagu pembukaDi Doa Ibuku Namaku Disebut oleh NikitaLagu penutupDi Doa Ibuku Namaku Disebut oleh NikitaNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode14ProduksiProduser eksekutifElly Yanti ...

District in Karnali province, Nepal District in NepalJajarkotDistrictLocation of Jajarkot District (dark yellow) in KarnaliCountry NepalEstablished2016Admin HQ.KhalangaGovernment • TypeCoordination committee • BodyDCC, JajarkotArea • Total2,230 km2 (860 sq mi)Population (2011) • Total171,304 • Density77/km2 (200/sq mi)Time zoneUTC+05:45 (NPT)Websiteddcjajarkot.gov.np Jajarkot District (Nepali: जाज�...

Arena Bola BasketThe Marshmallow[butuh rujukan]Arena Bola Basket pada April 2012LokasiTaman OlimpiadeStratfordLondonBritania RayaKoordinat51°32′55″N 0°00′50″W / 51.5486°N 0.0139°W / 51.5486; -0.0139Koordinat: 51°32′55″N 0°00′50″W / 51.5486°N 0.0139°W / 51.5486; -0.0139OperatorOlympic Delivery AuthorityKapasitas12,000Luas11,500 sq mKonstruksiMulai pembangunanOktober 2009; 14 tahun lalu (2009-10)Didir...
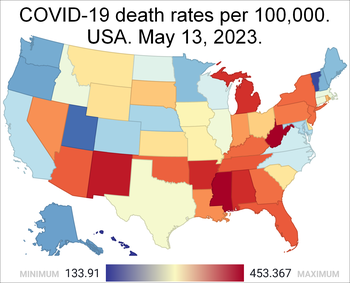
COVID-19 pandemic in the United StatesCOVID-19 cases per 100,000 people by state, as of July 11, 2022DiseaseCOVID-19Virus strainSARS-CoV-2LocationUnited StatesFirst outbreakWuhan, Hubei, China[1]Arrival dateJanuary 13, 2020[2](4 years, 4 months and 3 days ago) Public health emergency: 31 January 2020 – 11 May 2023 (3 years, 3 months, 1 week and 4 days)Confirmed cases103,436,829[3]Suspected cases‡146,585,169 (CDC estimate in Septe...

Pour les articles homonymes, voir Faguet. Émile Faguet Données clés Nom de naissance Auguste Émile Robin Faguet Naissance 17 décembre 1847 La Roche-sur-Yon Décès 7 juin 1916 (à 68 ans) Paris Activité principale écrivain français Distinctions membre de l’Académie françaisePrix Montyon (1887)Prix Vitet (1892) Auteur Langue d’écriture français Genres critique littéraire modifier Auguste Émile Faguet, né le 17 décembre 1847 à La Roche-sur-Yon[1] et mort le 7 juin 191...

Didone abbandonataOpera seria by Tomaso AlbinoniMarianna Bulgarelli, who created the title roleLibrettistPietro MetastasioLanguageItalianBased onDidone abbandonataPremiere26 December 1724 (1724-12-26)Teatro San Cassiano, Venice Didone abbandonata (Dido Abandoned) was an opera in three acts composed by Tomaso Albinoni. Albinoni's music (now lost) was set to Pietro Metastasio's libretto, Didone abbandonata, which was in turn based on the story of Dido and Aeneas from the fourth b...

Berikut ini adalah daftar divisi Angkatan Darat Amerika Serikat dan Korps Marinir Amerika Serikat pada Perang Dunia II. Amerika Serikat memulai perang dengan hanya beberapa divisi aktif: lima divisi infanteri dan satu divisi kavaleri. Pada akhir perang, Amerika Serikat telah menerjunkan hampir seratus divisi.[1] Angkatan Darat Divisi Lintas Udara Divisi Lintas Udara Lambang Nama Diaktifkan Memasuki Pertempuran Total hari dalam Pertempuran Panglima Kampanye Militer Divisi Lintas Udara ...

乌勒齐巴亚尔·杜伦巴亚尔出生1994年7月31日 (29歲)職業柔道家 乌勒齐巴亚尔·杜伦巴亚尔(蒙古語:Өлзийбаярын Дүүрэнбаяр,1996年1月31日—),蒙古男子柔道运动员,2014年亚洲运动会男子100公斤以上级银牌得主、2018年亚洲运动会男子100公斤以上级银牌得主、2018年世界柔道锦标赛男子100公斤以上级铜牌得主。[1] 参考资料 ^ Duurenbayar ULZIIBAYAR / IJF.org....

Championnat de Guyane de football 2017-2018 Généralités Sport Football Organisateur(s) Ligue de football de la Guyane Édition 56e Lieu(x) Guyane Date Du 14 septembre 2017 - 16 juin 2018 Participants 13 équipes Site web officiel guyane-foot.fff.fr Palmarès Tenant du titre US Matoury Vainqueur ASC Le Geldar Deuxième AS Étoile de Matoury Troisième US Matoury Navigation Édition précédente Édition suivante modifier La saison 2017-2018 est la cinquante-sixième édition du Championnat...

For other uses, see Alemannia (disambiguation). Alemania redirects here. For the European country which is sometimes translated to Alemania, see Germany. Former territory inhabited by the Germanic Alemanni peoples Kingdom of AlamanniaKönigreich Alamannien (German)Regnum Alamanniae (Latin)213–911Alemannia (orange) and Upper Burgundy (green) in the 10th centuryStatusPart of the Frankish Empire (496, 539–843), the Ostrogothic Kingdom (496–539), and East Francia (843–911)Govern...