SL2(R)
|
Read other articles:

Fula (Fulani atau Fulɓe) Wanita Fula di Provinsi Timur KamerunJumlah populasica. 25 juta jiwa[1][2]Daerah dengan populasi signifikanAfrika Barat dan Afrika Tengah Nigeria15.400.000[3][4] Guinea5.070.160[5] Senegal3.182.300[6] Mali2.870.000[7] Kamerun2.344.000[8] Niger2.046.330[9] Burkina Faso1.920.050[10] Mauritania916.113[11] Benin750.000[8] Guine...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Kuta Rock City – berita · surat kabar · buku · cendekiawan · JSTOR Kuta Rock CityAlbum studio karya Superman Is DeadDirilisJuli 2003Direkam2003GenrePunk rock, Pop punkLabelSony Music IndonesiaKronologi Su...

Republik Tanjung VerdeRepública de Cabo Verde (Portugis) Bendera Lambang Semboyan: Unidade, Trabalho, Progresso(Portugis: Persatuan, Pekerjaan, Kemajuan)Lagu kebangsaan: Cântico da LiberdadeIbu kota(dan kota terbesar)Praia14°55′N 23°31′W / 14.917°N 23.517°W / 14.917; -23.517Bahasa resmiPortugisPemerintahanRepublik semi-presidensial• Presiden José Maria Neves• Perdana Menteri Ulisses Correia e Silva LegislatifAssembleia NacionalKemerde...

لمعانٍ أخرى، طالع هوبارت (توضيح). هوبارت الإحداثيات 42°22′17″N 74°40′07″W / 42.3714°N 74.6686°W / 42.3714; -74.6686 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ديلاوير خصائص جغرافية المساحة 1.307515 كيلومتر مربع1.307513 كيلومتر مربع (1 أبري...

Our Love StoryNama lainHangul연애담 Alih Aksara yang DisempurnakanYeon-ae-dam SutradaraLee Hyun-juProduserKim Bo-raKim Tae-kyunLee Ji-seungLim Charn-sangPark Heon-sooDitulis olehLee Hyun-juPemeranLee Sang-heeRyu Sun-youngPenata musikChoi Yong-rakSinematograferKwon Yong-jikPenyuntingLee Hyun-juPerusahaanproduksiKorean Academy of Film ArtsDistributorIndie PlugTanggal rilis 01 Mei 2016 (2016-05-01) (JIFF) 17 November 2016 (2016-11-17) (Korea SElatan) Durasi99 men...

Gert-Jan Segers Gert Jan Maarten (Gert-Jan) Segers (lahir 9 Juli 1969 di Lisse) adalah seorang politikus Belanda. Sebagai anggota UniKristen (CU), dia adalah anggota Dewan Perwakilan dari 20 September 2012 hingga 24 Januari 2023. Referensi Drs. G.J.M. (Gert-Jan) Segers Diarsipkan 2020-10-09 di Wayback Machine., Parlement.com lbs Anggota Tweede Kamer (2021–2023)31 Maret 2021 – 6 Desember 2023Partai Rakyat untuk Kebebasan dan Demokrasi (VVD – 34) Hermans Aartsen <Van Ark> Becker Bev...

2022 concert tour by Kid Cudi A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (July 2022) (Learn how and when to remove this template message) To the Moon World TourTour by Kid CudiLocation Asia Europe North America Associated albumMan on the Moon III: The ChosenStart dateAugust 16, 2022End dateNovember 22, 20...

This article needs to be updated. Relevant discussion may be found on the talk page. Please help update this article to reflect recent events or newly available information. (October 2022) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Patten University – news · newspapers · books · scholar · JSTOR (October...

Raja Portugal dan Algarve Bekas Kerajaan Lambang Royal Manuel II Penguasa pertama D. Afonso I Penguasa terakhir D. Manuel II Gelar Gaya monarki Portugis Penunjuk Turun-temurun Pendirian 25 Juli 1139 Pembubaran 5 Oktober 1910 Penuntut takhta Duarte Pio, Pangeran Braganza Berikut ini adalah daftar raja Portugal. Kerajaan Portugal merdeka dari Kerajaan León. Kemudian pada tahun 1094, puteri Raja Alfonso VI dari León, Teresa, menikah dengan Henri dari Burgundia, yang sejak tahun 1096 bergelar ...

Pemandangan Ta' Qali dari Mdina Ta' Qali adalah sebuah lapangan terbuka di kawasan Attard di tengah Malta, yang terdiri dari stadion sepak bola nasional, Taman Nasional Ta' Qali, sebuah desa kerajinan, dan sebuah pasar sayuran nasional yang dikenal sebagai Pitkalija. Kedubes AS yang baru dibangun berada di seberang Taman Nasional Ta'Qali.[1] Pada Juli 2011, kedubes tersebut berpindah ke Ta'Qali dari Floriana dimana kedubes tersebut berdiri nyaris lima puluh tahun.[2] Referensi...

Farrington FieldFarrington Field in Fort Worth, TexasLocation1501 N. University Dr.Fort Worth, TexasCoordinates32°44′45″N 97°21′37″W / 32.745743°N 97.360218°W / 32.745743; -97.360218OwnerFort Worth ISDCapacity18,500Record attendance24,836 (November 23, 1944 North Side H.S. vs. Paschal H.S.)SurfaceartificialConstructionBuilt1938–1939OpenedNovember 3, 1939Renovated2010Construction cost$400,000ArchitectPreston M. GerenGeneral contractorGeneral Construction C...

The member-states of the European Union by the European parliamentary affiliations of their leaders, as of 1 January 2006. This article describes the party affiliations of the leaders of each member-state represented in the European Council during the year 2006. The list below gives the political party that each head of government, or head of state, belongs to at the national level, as well as the European political alliance to which that national party belongs. The states are listed from mo...

After Hours til Dawn TourThe Weeknd al Foro Sol di Città del Messico nel 2023Tour di The WeekndAlbumAfter Hours e Dawn FM Inizio Filadelfia 14 luglio 2022 Fine Guadalajara 25 ottobre 2023 Tappe3 Spettacoli21 in Nord America30 in Europa13 in America Latina64 totali Cronologia dei tour di The Weeknd The Weeknd Asia Tour(2018) L'After Hours til Dawn Tour, noto precedentemente come The After Hours Tour, è il sesto tour musicale del cantante canadese The Weeknd, a supporto dei suoi quarto e ...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2023) المنطقة الدبلوماسية المنطقة الدبلوماسية منطقة الاسم الرسمي المنطقة الدبلوماسية (البحرين) الإحداثيات 26°14�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2012. ArmançonCiri-ciri fisikMuara sungaiYonnePanjang202 kmLuas DASDAS: 2,990 km² Sungai Armançon mengaliri wilayah barat laut Burgundia di Prancis. Bermuara di département Côte-d'Or dan mengalir ke Yonne (tepi kanan) di Migennes. Bermuara di ketinggian 3...

Rough, unfinished woollen fabric, of a soft, open texture This article is about the cloth. For the river in Scotland and England, see River Tweed. For other uses, see Tweed (disambiguation). Harris Tweed woven in a herringbone twill pattern, mid-20th century Tweed is a rough, woollen fabric, of a soft, open, flexible texture, resembling cheviot or homespun, but more closely woven. It is usually woven with a plain weave, twill or herringbone structure. Colour effects in the yarn may be obtaine...
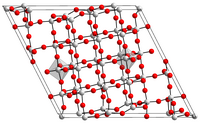
Pentossido di niobioStruttura di Lewis del pentossido di niobio Struttura 3D sfere-stecche del pentossio di niobio Struttura 3D van der Waals del pentossido di niobio Nome IUPACOssido di niobio (V) [1] Caratteristiche generaliFormula bruta o molecolareNb2O5 Massa molecolare (u)265,81 g/mol Aspettosolido biancastro Numero CAS1313-96-8 Immagine_3D Numero EINECS215-213-6 PubChem123105 e 16218255 SMILESO=[Nb](=O)O[Nb](=O)=O Proprietà chimico-fisicheDensità (g/cm3, in c.s.)4,5 (20 °C) S...

Pondok Pesantren LirboyoAlamatKelurahan Lirboyo, Kecamatan MojorotoKota Kediri, Jawa Timur64117Koordinat7°49′05″S 111°59′25″E / 7.818048202980707°S 111.99037166686124°E / -7.818048202980707; 111.99037166686124Koordinat: 7°49′05″S 111°59′25″E / 7.818048202980707°S 111.99037166686124°E / -7.818048202980707; 111.99037166686124Telepon/Faks.0354 773608 0354 7417885 081292272019Situs weblirboyo.netInformasiJenisPondok pesa...



![{\displaystyle [x,1]\mapsto [x,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\ =\ [ax+b,\ cx+d]\ =\,\left[{\frac {ax+b}{cx+d}},\ 1\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac9fecb3b29c144f054189bc958c230949c38129)





















