Schur multiplier
|
Read other articles:

Michel Navratil Jr.Lahir(1908-06-12)12 Juni 1908Nice, PrancisMeninggal30 Januari 2001(2001-01-30) (umur 92)Montpellier, PrancisOrang tuaMichel Navratil dan Marcelle Caretto Michel Marcel Navratil, Jr. (12 Juni 1908 – 30 Januari 2001) adalah salah satu korban selamat terakhir dari tenggelamnya kapal RMS Titanic pada tanggal 15 April 1912. Michel, bersama dengan saudaranya, Edmond Navratil (1910-1953), dikenal sebagai Yatim Titanic, karena merupakan hanya satu-satunya anak...

Gereja Konvensi Baptis SelatanSingkatanSBCPenggolonganProtestanOrientasiGereja BaptisTeologiEvangelikalBentukpemerintahanKongregasionalPresidenJ.D. GreearWilayahUnited StatesDidirikan8–12 Mei 1845 Augusta, GeorgiaTerpisah dariTriennial Convention (1845)PecahanAmerican Baptist AssociationAlliance of BaptistsCooperative Baptist FellowshipJemaat47,272 (2016)Umat15.00 juta (2017) Weekly Attendance = 5,200,716[1]Situs web resmiwww.sbc.net Gereja Konvensi Baptis Selatan (bahasa Inggris: S...

Cokelat susuCokelat susu batanganJenisMakanan manisTempat asal SwissDibuat olehDaniel PeterDiciptakan tahun1875Bahan utama Mentega kakao Biji kakao Susu Gula Sunting kotak info • L • BBantuan penggunaan templat ini Media: Cokelat susu Cokelat susu adalah cokelat padat yang mengandung kakao, gula, dan susu. Cokelat susu awalnya dijual dan dikonsumsi sebagai minuman pada zaman pra-Kolumbus, dan setelah diperkenalkan ke Eropa Barat. Produsen utama cokelat susu dianta...

American politician Stanley R. TupperMember of the U.S. House of Representativesfrom Maine's 1st districtIn officeJanuary 3, 1963 – January 3, 1967Preceded byPeter A. GarlandSucceeded byPeter KyrosMember of the U.S. House of Representativesfrom Maine's 2nd districtIn officeJanuary 3, 1961 – January 3, 1963Preceded byFrank M. CoffinSucceeded byClifford G. McIntire Personal detailsBornStanley Roger Tupper(1921-01-25)January 25, 1921Boothbay Harbor, ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Eboraphyllus middletoni Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Eboraphyllus Spesies: Eboraphyllus middletoni Eboraphyllus middletoni adalah spesies kumbang tanduk panjang yan...

Pour les articles homonymes, voir Union sacrée. L'Union sacrée est le nom donné au mouvement de rapprochement politique qui a soudé les Français de toutes tendances (politiques ou religieuses) lors du déclenchement de la Première Guerre mondiale. Le terme fut utilisé pour la première fois à la Chambre des députés le 4 août 1914, par le président de la République, Raymond Poincaré, dans son message aux Assemblées. Cela fut le cas immédiatement car l’ensemble des organisati...

Holly SampsonSampson berpose di film guru seks pertamakuLahirHolly Joy Sampson[1]4 September 1973 (umur 50)[1]Prescott, Arizona, A.S.[1]Nama lainNicolette[1]Nicolete[1]Nicolette Foster[1]Andrea Michaels[1]Zoe[1]Tinggi5 ft 5 in (1,65 m)[1] Holly Joy Sampson (lahir 4 September 1973), juga dikenl dengans sebutan Nicolette Foster, Andrea Michaels atau Zoe[1] adalah seorang aktris dan model as...

Territorio dello Utah e delle aree vicine nel momento della fondazione. Sono visibili i confini degli stati nei quali poi è stato suddiviso Il Territorio dello Utah fu un territorio organizzato degli Stati Uniti d'America che esistette dal 9 settembre 1850 al 4 gennaio 1896, quando quello che restava del territorio fu incorporato nello Stato federale col nome di Stato dello Utah. Storia Il territorio fu definito con una legge del Congresso il 9 settembre 1850, lo stesso giorno in cui lo Stat...
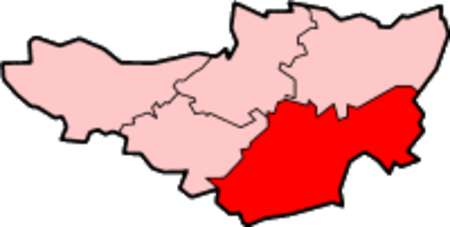
Human settlement in EnglandAnsfordAnsford from Ditcheat HillAnsfordLocation within SomersetPopulation1,175 (2021)[1]OS grid referenceST640328Civil parishAnsfordUnitary authoritySomerset CouncilCeremonial countySomersetRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townCastle CaryPostcode districtBA7Dialling code01963PoliceAvon and SomersetFireDevon and SomersetAmbulanceSouth Western UK ParliamentSomerton and Frome List of ...

Questa voce sull'argomento centri abitati dei Paesi Bassi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Renkumcomune Renkum – Veduta LocalizzazioneStato Paesi Bassi Provincia Gheldria AmministrazioneCapoluogoOosterbeek TerritorioCoordinatedel capoluogo51°58′59.88″N 5°51′00″E / 51.9833°N 5.85°E51.9833; 5.85 (Renkum)Coordinate: 51°58′59.88″N 5°51′00″E...

EthnologueHistoireFondation 1951CadreType Publication scientifiquePays États-UnisOrganisationPropriétaire SIL InternationalSite web (en) www.ethnologue.commodifier - modifier le code - modifier Wikidata Ethnologue, Languages of the World, souvent abrégé en Ethnologue, est une publication de SIL International visant à inventorier toutes les langues du monde. Publiée en version sur papier depuis 1951, elle est également disponible sur internet depuis 1997. Historique La premi...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2019) تحتوي هذه المقالة على قائمة الهيئات الحكومية الجزائرية بأنواعها والتي تم إنشاؤها في الجزائر، والتي تخص الهيئات الدستورية والوطنية والإدارية. الحالية الهي...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Canadian singer-songwriter (born 1979) Ariane MoffattBackground informationBorn (1979-04-26) 26 April 1979 (age 45)Saint-Romuald, Quebec, CanadaInstrument(s)Piano, guitar, drums, synthesizerLabelsAudiogramWebsitearianemoffatt.comMusical artist Ariane Moffatt (born 26 April 1979) is a Canadian singer-songwriter. Known for working across multiple musical genres, Moffatt's music combines elements of electronica, jazz, folk, and pop. A francophone, she is bilingual and has recorded tracks in...

Sultan of the Seljuk Empire from 1118 to 1157 Sanjar redirects here. For the town in Iraq, see Sinjar. For the Iraqi plain, see Plain of Sanjar. For the Iraqi mountain, see Mount Sinjar. Ahmad SanjarAhmad Senjer seated on his throne, in a 1307 Ilkhanid miniature.Sultan of the Great Seljuq EmpireReign18 April 1118 – 8 May 1157PredecessorMuhammad ICo-sultanMahmud II(1118–1131)Dawud(1131–1132)Tughril II(1132–1134)Mas'ud(1134–1152)Malik-Shah III(1152–1153)Muhammad II(1153–1157)Malik...

Yehudi Menuhin Nazionalità Stati Uniti Svizzera GenereMusica classica Periodo di attività musicale1923 – 1999 Strumentoviolino Sito ufficiale Modifica dati su Wikidata · Manuale Premio Wolf per le arti 1991Sir Yehudi Menuhin, barone Menuhin[1][2] (New York City, 22 aprile 1916 – Berlino, 12 marzo 1999), è stato un violinista statunitense con cittadinanza britannica naturalizzato svizzero. Nativo degli Stati Uniti, trascorse gran parte ...

Луганська область Герб Луганської області Прапор Луганської області Основні дані Прізвисько: ЛуганщинаСхідна брама УкраїниСвітанок України, Слобожанщина, Донбас, Країна: Україна Утворена: 3 червня 1938 року Код КАТОТТГ: UA44000000000018893 Населення: 2 167 802 Площа: 26 684 км...

ميرينا Μύρινα Myrina خريطة الموقع تقسيم إداري البلد اليونان[1] المنطقة الإدارية شمال إيجة ليسبوس خصائص جغرافية إحداثيات 39°52′42″N 25°03′49″E / 39.8782°N 25.0636°E / 39.8782; 25.0636 الأرض 82.094 كم² السكان التعداد السكاني 7,602 نسمة (إحصاء 2001) الكثافة السكانية 92 الرمز الجغ...

Village in New York, United StatesPort Washington North, New YorkVillageIncorporated Village of Port Washington NorthSoundview Drive in the Soundview Village section of Port Washington North in 2021 Official Emblem of Port Washington NorthNickname(s): Port North, Soundview, The ViewLocation in Nassau County and the state of New YorkPort Washington North, New YorkLocation on Long IslandShow map of Long IslandPort Washington North, New YorkLocation within the state of New YorkShow map of ...













![{\displaystyle S\leq [F,R]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f90030a354c16b2b77ce87855971d0ff9501c80)

![{\displaystyle H_{2}(G,\mathbb {Z} )\cong (R\cap [F,F])/[F,R]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b119b72ed337e16e5c25110fd2d7a9e54ce096d5)


