Dihedron
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Отдельная дивизия Офицеры Отдельной дивизии Годы существования 1921-1922 Страна Греция Участие в Вторая греко-турецкая война Медиафайлы на Викискладе Отдельная дивизия или Независимая дивизия (греч. Ανεξάρτητη Μεραρχία) — дивизия греческой армии, сформированная ...

Under the Sun of SatanPoster film pertamaSutradara Maurice Pialat Produser Claude Abeille Daniel Toscan du Plantier Ditulis oleh Sylvie Danton Maurice Pialat SkenarioSylvie DantonMaurice PialatBerdasarkanUnder the Sun of Satan karya Georges BernanosPemeran Gérard Depardieu Sandrine Bonnaire Maurice Pialat Penata musikHenri DutilleuxSinematograferWilly KurantPenyuntingYann DedetTanggal rilis 14 Mei 1987 (1987-05-14) (Cannes) 2 September 1987 (1987-09-02) Durasi93 menitNega...

British peer and politician Colonel His GraceThe Duke of WellingtonKG GCVO DLMember of the House of LordsLord TemporalIn office8 June 1900 – 18 June 1934Hereditary PeeragePreceded byThe 3rd Duke of WellingtonSucceeded byThe 5th Duke of Wellington Personal detailsBorn(1849-03-15)15 March 1849Died18 June 1934(1934-06-18) (aged 85)Political partyConservativeSpouseKathleen Emily Bulkeley WilliamsChildrenLady Evelyn Wellesley Arthur Wellesley, 5th Duke of WellingtonLord Ric...

French painter This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Jean Le Moal – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this template message) Jean Le Moal in 1985 Jean Le Moal (30 October 1909 – 16 March 2007) was a French painter of the new Paris school, des...

American lawyer and government official (1905–1976) John GrahamGraham (left) with Paul F. Foster (center) and John A. McCone, 1960Commissioner of Internal RevenueIn officeNovember 19, 1952 – January 19, 1953PresidentHarry S. TrumanPreceded byJohn DunlapSucceeded byJustin Winkle (Acting) Personal detailsBornJohn Stephens Graham(1905-08-04)August 4, 1905Reading, Massachusetts, U.S.DiedOctober 20, 1976(1976-10-20) (aged 71)Washington, D.C., U.S.Political partyDemocraticSpouseEl...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Lambang negara – berita · surat kabar · buku · cendekiawan · JSTOR Perisai Penopang Hiasan kepala Rangkaian bunga Mantel Pelindung kepala Moto Bagian-bagian lambang negara pada umumnya Lambang negara, di...

Overview of Brown University in popular culture Brown University is a private research university in Providence, Rhode Island. Like other members of the Ivy League, it is known for prestige, academic rigor and selective undergraduate admissions process. Among its peers, Brown is noted for a culture of campus activism and longstanding commitment to academic and intellectual freedom exemplified by its Open Curriculum and course shopping period.[1][2][3] The university ha...

This article is about the demographic features of the population of Pakistan. For a general overview of the citizens of Pakistan, see Pakistanis. Demographics of PakistanPopulation pyramid of Pakistan as of July 1, 2021Population241,492,197 (2023 census)Density260.8/km2 (675/sq mi)248.9/km2 (645/sq mi) (including AJK and GB)Growth rate 1.85% (2021 est.)[1]Birth rate22.5 births / 1,000 population (2023 est.)Death rate7.2 deaths / 1,000 population (2021 est.)[1]Life ex...

Motorsport track in the United States Pocono RacewayThe Tricky TriangleLocationLong Pond Road and Andretti Road, Long Pond, Pennsylvania, 18334Time zoneUTC−5 / −4 (DST)Capacity76,812OwnerMattco Inc.OperatorIgdalsky and Mattioli familiesBroke ground1968Opened1968ArchitectRodger WardFormer namesPocono International Raceway (1968–1984)Major eventsCurrent:NASCAR Cup SeriesHighPoint.com 400 (1971–present)NASCAR Xfinity SeriesExplore the Pocono Mountains 225 (2016–present)NASCAR Craftsman...
Bahasa Gilaki گیلکی Giləki Dituturkan di Iran WilayahPesisir barat daya Laut KaspiaPenutur2.4 juta (2016)Rumpun bahasaIndo-Eropa Indo-IranIranIran BaratIran Barat LautKaspiaGilaki DialekGilaki Barat Gilaki Timur Galeshi Kode bahasaISO 639-3glkGlottologgila1241[1]Linguasfer58-AAC-ebLokasi penuturanArea tempat Gilaki digunakan sebagai bahasa ibuPeta bahasa lain Artikel ini mengandung simbol fonetik IPA. Tanpa bantuan render yang baik, Anda akan melihat tanda tanya,...

North-south avenue in Manhattan, New York City Template:Attached KML/Ninth Avenue (Manhattan)KML is from Wikidata Ninth AvenueColumbus Avenue (59th–110th Streets)Morningside Drive (north of 110th Street)The avenue in Hell's KitchenOwnerCity of New YorkMaintained byNYCDOTLength5.7 mi (9.2 km)[1]LocationManhattan, New York CitySouth endGreenwich StreetNorth endBroadway above West 220th Street in Inwood, ManhattanEastEighth Avenue (below 59th Street)Central Park Wes...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sword bayonet – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) A sword bayonet is any long, knife-bladed bayonet designed for mounting on a musket or rifle. Its use is thought to have begun in the 18th century and...

Gallery in Bukit Katil, Malacca, Malaysia Rumah MelakaRumah MelakaGeneral informationTypeGalleryLocationBukit Katil, Malacca, MalaysiaAddressLot 233 & 234 Jalan Tun Kudu, Bukit Katil, 75450 Melaka.Coordinates2°13′47.7″N 102°18′05.3″E / 2.229917°N 102.301472°E / 2.229917; 102.301472CostMYR5 millionOwnerMalaysian Timber Industry BoardManagementMalaysian Timber Industry BoardGrounds5 hectares Rumah Melaka (lit. 'Malacca House') is a gallery owned...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Harper University Hospital – news · newspapers · books · scholar · JSTOR (August 2017) (Learn how and when to remove this template message) Hospital in Michigan, United StatesHarper University HospitalDetroit Medical CenterHarper HospitalGeographyLocationDetroi...
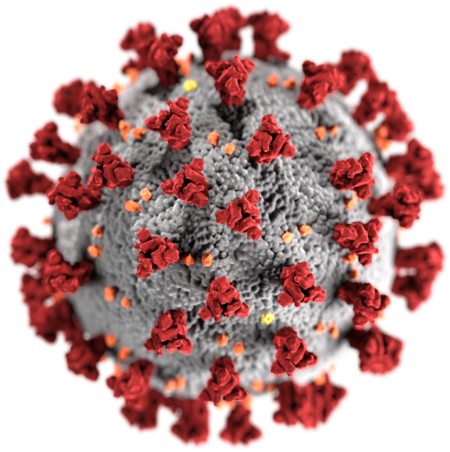
Data klinis Kat. kehamilan ? Status hukum Penggunaan darurat di Tiongkok, Indonesia, Brasil, dan Turki Rute Penyuntikan intraotot Pengenal Kode ATC None DrugBank DB15806 Data kimia Rumus ? Bagian dari seri artikel mengenaiPandemi Covid-19Permodelan atomik akurat yang menggambarkan struktur luar virus SARS-CoV-2. Tiap bola yang tergambarkan di sini adalah sebuah atom. SARS-CoV-2 (virus) Covid-19 (penyakit) Kronologi2019 2020 Januari Februari Maret April Mei Juni Juli Agustus September Oktober ...

Closed railway in Aberdeenshire, Scotland Deeside RailwayThe disused line, east of Ballater, in 2008OverviewLocaleScotlandDates of operation1853–1967TechnicalTrack gauge1,435 mm (4 ft 8+1⁄2 in) Route map Legend Great North of Scotland Railwayto Inverness Aberdeen Joint Great North of Scotland Railwayto Perth Holburn Street Ruthrieston Pitfodels Cults West Cults Bieldside Murtle Milltimber Culter Drum Park Mills of Drum Crathes Mil...

This article is about Örebro SK's bandy section. For other sections of the club, see Örebro SK (disambiguation). Ice hockey team in Örebro, SwedenÖrebro SK BandyCityÖrebro, SwedenLeagueAllsvenskanFounded1908; 115 years ago (1908)Home arenaBehrn ArenaHead coachTomas Rosdahl Örebro SK Bandy is the Bandy section of sports club Örebro SK, from Örebro, Sweden. Örebro were founded in 1908 and play their home games indoors at Behrn Arena. The club play in Allsvenskan, the ...

Painting by Klimt Portrait of a LadyArtistGustav KlimtYear1916–1917MediumOil on canvasDimensions60 cm × 55 cm (24 in × 22 in)LocationGalleria d'arte moderna Ricci Oddi, Piacenza Portrait of a Lady is an oil on canvas painting by Gustav Klimt, painted between 1916 and 1917. The painting measures 60 by 55 centimetres (24 in × 22 in). It depicts a portrait of a female figure, composed in an unusually lively expressionistic style. It w...

Zobacz też: inne artykuły o drogach krajowych nr 42. Początek drogi Kamienna 39 Koniec drogi Rudnik 9 E371 Długość 274 km Województwa opolskie,śląskie,łódzkie,świętokrzyskie Mapa Zdjęcie Działoszyn – most przez Wartę w ciągu drogi krajowej 42 Przebieg trasy Legenda w użyciu projekt, budowa, konieczność modernizacji węzeł drogowy typu WA węzeł drogowy typu WB skrzyżowanie rondo przejście granicznepunkt poboru opłat (PPO) stacja poboru opłat (SPO) most / wia...

Maria RessaThông tin chungSinh2 tháng 10, 1963 (60 tuổi)Manila, PhilippinesHọc vấnĐại học Princeton (cử nhân)Đại học Philippines DilimanNghề nghiệpPhóng viên, tác giaTrang web chính thứcRapplermariaressa.com Maria Angelita Ressa (sinh ngày 2 tháng 10 năm 1963) là một nhà báo và tác giả người Mỹ gốc Philippines, nổi tiếng với việc đồng sáng lập Rappler, là giám đốc điều hành của tờ báo.[1] Trước đây...