Rhombicuboctahedron
| |||||||||||||||||||||||||||||||
Read other articles:

Occitano occitan, lenga d'òcHablado en FranciaEspaña EspañaItalia Italia MónacoRegión OccitaniaHablantes entre 2 millones hasta 12 millones, según fuentes[1]Familia Indoeuropeo Itálico Romance Romance occidental Occitano-romance OccitanoEscritura alfabeto latino, norma clásica del occitano, norma mistral...

Guillaume PatryKebangsaanKanada Guillaume Patry adalah pemain StarCraft profesional asal Kanada yang bermain dibawah alias Grrrr... Ia berasal dari Kota Quebec,[1] adalah juara dunia StarCraft pada tahun 1999.[2] Ia adalah panelis pada acara bincang-bincang Non-Summit[3] Referensi ^ Transcription de : Guillaume Patry : Maître de StarCraft. Diarsipkan dari versi asli tanggal 2012-10-21. Diakses tanggal 2010-11-27. Parameter |url-status= yang tidak ...

Gereja Tritunggal Kudus, Stratford-upon-AvonGereja dari barat dayaNegaraBritania RayaDenominasiGereja InggrisKegerejaanBroad ChurchSitus webwww.stratford-upon-avon.org/index.htmlSejarahDedikasiTritunggal KudusAdministrasiParokiStratford-upon-AvonKeuskupanCoventryProvinsiCanterburyKlerusVikarisPatrick Taylor[1]Pendeta PembantuKay Dyer[1] The Collegiate Church of the Holy and Undivided Trinity, Stratford-upon-Avon adalah sebuah gereja paroki terdaftar[2] Tingkat 1 dari G...

Policy on permits required to enter Australia and its external territories This article is part of a series on thePolitics ofAustralia Constitution The Crown Monarch Charles III Governor-General David Hurley Executive Prime Minister Anthony Albanese (ALP) Deputy Prime Minister Richard Marles (ALP) Federal Executive Council Ministry Albanese ministry Cabinet Legislature Australian Parliament Senate President Sue Lines (ALP) Leader Penny Wong (ALP) House of Representatives Speaker Milton Dick (...
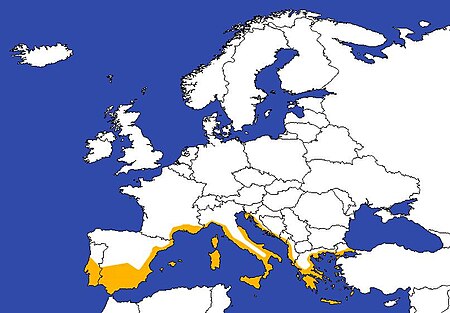
أوروبا الجنوبيةمعلومات عامةجزء من أوروبا تقع في منطقة تضاريس أوروبا الإحداثيات 41°05′37″N 15°01′01″E / 41.093498°N 15.017008°E / 41.093498; 15.017008 لديه جزء أو أجزاء ألبانيا[1]أندورا[1]البوسنة والهرسك[1] تعديل - تعديل مصدري - تعديل ويكي بيانات تشير التسمية جنوب أوروبا عمو...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

American actor Joel CrothersPublicity Photo of Joel CrothersBornJoel Anthony Crothers(1941-01-28)January 28, 1941Cincinnati, Ohio, U.S.DiedNovember 6, 1985(1985-11-06) (aged 44)Los Angeles, California, U.S.EducationBirch Wathen SchoolAlma materHarvard UniversityOccupationActor Joel Anthony Crothers (January 28, 1941 – November 6, 1985) was an American actor. His credits primarily included stage and television work, including a number of soap opera roles, the best known being Miles...

Sepasang gambar Men Shen menghiasi pintu kuil di Taichung, Taiwan. Artikel ini mengenai kebudayaan China. Lihat pula Janus, dewa pintu Romawi. Men Shen (t=門神; s=门神; pinyin=ménshén; Hokkien= Mui Sin) merupakan Dewa Pintu dalam tradisi China. Biasanya lukisan keduanya ditempelkan pada daun pintu masuk kuil, rumah, kantor, dan sebagainya supaya roh jahat tidak berani masuk. Men Shen selalu berjumlah sepasang, saling berhadapan; jika digambarkan saling membelakangi dipercaya akan membaw...

Rusalka oleh Ivan Bilibin, 1934 Dalam mitologi Slavia, rusalka adalah makhluk perempuan yang hidup di air. Menurut sebagian besar tradisi, rusalka merupakan perempuan ikan, yang tinggal di dasar sungai. Rusalka berasal dari para perempuan yang meninggal di sungai. Pada tengah malam para rusalka muncul dari dalam sungai lalu menari dan menyanyi untuk memikat para pria yang lewat. Pria yang terpikat oleh rusalka akan berjalan ke sungai dan tenggelam. Ada juga rusalka yang memikat pria dengan me...

Ethnolinguistic group in Pakistan For the ethnic group in Vietnam, see K'ho people. KhoکھوChitrali men along with Mehtar Fateh-ul-Mulk Ali Nasir, the current head of the Katoor DynastyTotal populationc. 800,000 (2021)[1]Regions with significant populationsChitral and Gilgit BaltistanLanguagesKhowarReligionPredominantly Hanafi Sunni Islam[2]Minority Ismaili Shia Islam[2]Related ethnic groupsOther Indo-Aryan peoples The Kho (/koʊ/,[3] Khowar: کھو) or...

Pour les articles homonymes, voir Zilli. Cet article est une ébauche concernant une chanteuse italienne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Nina Zilli Informations générales Surnom Nina Zilli Nom de naissance Maria Chiara Fraschetta Naissance 2 février 1980 (44 ans) Plaisance (Italie) Activité principale Auteure-compositrice-interprète Genre musical Funk, RnB, jazz, soul Années actives D...

UN resolution regarding Russian activities in Crimea This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: United Nations General Assembly resolution 73/194 – news · newspapers · books · scholar · JSTOR (March 2019) (Learn how and when to remove this message) United Nations resolution resolution adopted in 2018 UN General AssemblyResolution 73/194Date17 Decem...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Aspect of the English philosopher's teachings Portrait of Thomas Hobbes Thomas Hobbes’s moral and political philosophy is constructed around the basic premise of social and political order, explaining how humans should live in peace under a sovereign power so as to avoid conflict within the ‘state of nature’.[1] Hobbes’s moral philosophy and political philosophy are intertwined; his moral thought is based around ideas of human nature, which determine the interactions that make...

19th century German historian and promoter of Scientific Racism Christoph MeinersChristoph Meiners; portrait by Johann Heinrich Tischbein the Younger (c. 1772)Born(1747-07-31)July 31, 1747WarstadeDiedMay 1, 1810(1810-05-01) (aged 62)NationalityGermanEducationUniversity of GöttingenSchoolGöttingen school of historyInstitutionsUniversity of GöttingenMain interestsPolygenism Christoph Meiners (31 July 1747 – 1 May 1810) was a German racialist, philosopher, historian, and writer bor...

Kauri (Agathis australis) was extensively logged for its desirable timber. This surviving tree is called 'Te Matua Ngahere'. Forestry in New Zealand has a history starting with European settlement in the 19th century and is now an industry worth seven percent[citation needed] of annual revenue. Much of the original native forest cover was burnt off and logged, however forests have been extensively planted, predominantly with fast-growing cultivars of the Monterey Pine. Wood chips, wh...

Vowel sound represented by ⟨ʌ⟩ in IPA Open-mid back unrounded vowelʌIPA Number314Audio sample source · helpEncodingEntity (decimal)ʌUnicode (hex)U+028CX-SAMPAVBraille Image IPA: Vowels Front Central Back Close i y ɨ ʉ ɯ u Near-close ɪ ʏ ʊ Close-mid e ø ɘ ɵ ɤ o Mid e̞ ø̞ ə ɤ̞ o̞ Open-mid ɛ œ ɜ ɞ ʌ ɔ Near-open æ ɐ Open a ɶ ä ɑ ɒ IPA help audio full chart template Legend: unrounded • rounded Spectrogram of ʌ The ope...

Pour les articles homonymes, voir Shirayuki. ShirayukiPhotographie de l'empereur Hirohito à cheval sur Shirayuki, dans les années 1930.BiographieNaissance 1921Haras de BábolnaDécès 25 octobre 1947Shimōsa Imperial Stock Farm (d)Propriétaire Hirohitomodifier - modifier le code - modifier Wikidata Shirayuki (白雪?), ou Shira-Yuki, ou encore Sirayuki (en japonais, « Neige blanche »), est un cheval que montait l'empereur du Japon Hirohito au début de l'ère Shōwa. Ce cheval...

此條目需要擴充。 (2018年7月22日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 此條目没有列出任何参考或来源。 (2018年7月22日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 CORBA(Common Object Request Broker Architecture)又叫通用物件請求代理...

Swiss watchmaker This article is about the watch company. For other uses of the term swatch, see Swatch (disambiguation). For the parent group, see The Swatch Group. Swatch Ltd.Swatch store in Namba, Osaka, JapanCompany typeSubsidiaryIndustryWatchmakingFounded1983; 41 years ago (1983)HeadquartersBiel, SwitzerlandKey peopleNick Hayek Jr. (chairman, president)ProductsWristwatchesParentThe Swatch GroupSubsidiariesFlik FlakWebsiteswatch.com Swatch is a Swiss watchmaker founded i...





































