三角恒等式
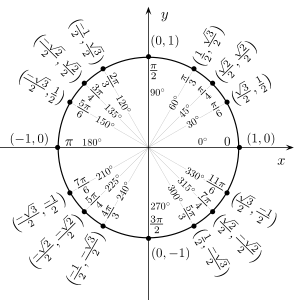
在几何上依据以O 为中心的单位圆可以构造角θ的很多三角函数 幾個三角函數的圖形,分別為正弦、餘弦、正切、餘切、正割、餘割和正矢。配色與上圖相同
单位圆 的角度在数学 中,三角恒等式 是对出现的所有值都为實变量 ,涉及到三角函数 的等式。这些恒等式 在表达式中有些三角函数需要简化的时候是很有用的。一个重要应用是非三角函数的积分 :一个常用技巧是首先使用使用三角函数的代换规则 ,则通过三角恒等式可简化结果的积分。
为了避免由于
sin
−
1
x
{\displaystyle \sin ^{-1}x}
三角函数 的倒数 和反函数 。另外在表示余割函数 時,'
csc
{\displaystyle \csc }
c
o
s
e
c
{\displaystyle \mathrm {cosec} }
不同的角度度量适合于不同的情况。本表展示最常用的系统。弧度是缺省的角度量并用在指数函数中。所有角度度量都是无单位的。另外在計算機中角度的符號為D,弧度的符號為R,梯度的符號為G。
相同角度的轉換表
角度單位
值
計算機中代號
轉
0
{\displaystyle 0}
1
12
{\displaystyle {\frac {1}{12}}}
1
8
{\displaystyle {\frac {1}{8}}}
1
6
{\displaystyle {\frac {1}{6}}}
1
4
{\displaystyle {\frac {1}{4}}}
1
2
{\displaystyle {\frac {1}{2}}}
3
4
{\displaystyle {\frac {3}{4}}}
1
{\displaystyle 1}
無
角度
0
∘
{\displaystyle 0^{\circ }}
30
∘
{\displaystyle 30^{\circ }}
45
∘
{\displaystyle 45^{\circ }}
60
∘
{\displaystyle 60^{\circ }}
90
∘
{\displaystyle 90^{\circ }}
180
∘
{\displaystyle 180^{\circ }}
270
∘
{\displaystyle 270^{\circ }}
360
∘
{\displaystyle 360^{\circ }}
D
弧度
0
{\displaystyle 0}
π
6
{\displaystyle {\frac {\pi }{6}}}
π
4
{\displaystyle {\frac {\pi }{4}}}
π
3
{\displaystyle {\frac {\pi }{3}}}
π
2
{\displaystyle {\frac {\pi }{2}}}
π
{\displaystyle \pi }
3
π
2
{\displaystyle {\frac {3\pi }{2}}}
2
π
{\displaystyle 2\pi }
R
梯度
0
g
{\displaystyle 0^{g}}
33
1
3
g
{\displaystyle 33{\frac {1}{3}}^{g}}
50
g
{\displaystyle 50^{g}}
66
2
3
g
{\displaystyle 66{\frac {2}{3}}^{g}}
100
g
{\displaystyle 100^{g}}
200
g
{\displaystyle 200^{g}}
300
g
{\displaystyle 300^{g}}
400
g
{\displaystyle 400^{g}}
G
三角函數間的關係,可分成正函數 餘函數 畢達哥拉斯三角恒等式如下:
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1\,}
tan
2
θ
+
1
=
sec
2
θ
{\displaystyle \tan ^{2}\theta +1\,=\sec ^{2}\theta }
1
+
cot
2
θ
=
csc
2
θ
{\displaystyle 1\,+\cot ^{2}\theta =\csc ^{2}\theta }
由上面的平方關係加上三角函數的基本定義,可以導出下面的表格,即每個三角函數都可以用其他五個表達。(严谨地说,所有根号前都应根据实际情况添加正负号)
函數
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
tan
{\displaystyle \tan }
cot
{\displaystyle \cot }
sec
{\displaystyle \sec }
csc
{\displaystyle \csc }
sin
θ
{\displaystyle \sin \theta }
sin
θ
{\displaystyle \sin \theta \ }
1
−
cos
2
θ
{\displaystyle {\sqrt {1-\cos ^{2}\theta }}}
tan
θ
1
+
tan
2
θ
{\displaystyle {\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}}
1
1
+
cot
2
θ
{\displaystyle {\frac {1}{\sqrt {1+\cot ^{2}\theta }}}}
sec
2
θ
−
1
sec
θ
{\displaystyle {\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}}
1
csc
θ
{\displaystyle {\frac {1}{\csc \theta }}}
cos
θ
{\displaystyle \cos \theta }
1
−
sin
2
θ
{\displaystyle {\sqrt {1-\sin ^{2}\theta }}}
cos
θ
{\displaystyle \cos \theta \ }
1
1
+
tan
2
θ
{\displaystyle {\frac {1}{\sqrt {1+\tan ^{2}\theta }}}}
cot
θ
1
+
cot
2
θ
{\displaystyle {\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}}
1
sec
θ
{\displaystyle {\frac {1}{\sec \theta }}}
csc
2
θ
−
1
csc
θ
{\displaystyle {\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}}
tan
θ
{\displaystyle \tan \theta }
sin
θ
1
−
sin
2
θ
{\displaystyle {\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}}
1
−
cos
2
θ
cos
θ
{\displaystyle {\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}}
tan
θ
{\displaystyle \tan \theta \ }
1
cot
θ
{\displaystyle {\frac {1}{\cot \theta }}}
sec
2
θ
−
1
{\displaystyle {\sqrt {\sec ^{2}\theta -1}}}
1
csc
2
θ
−
1
{\displaystyle {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}}
cot
θ
{\displaystyle \cot \theta }
1
−
sin
2
θ
sin
θ
{\displaystyle {{\sqrt {1-\sin ^{2}\theta }} \over \sin \theta }}
cos
θ
1
−
cos
2
θ
{\displaystyle {\cos \theta \over {\sqrt {1-\cos ^{2}\theta }}}}
1
tan
θ
{\displaystyle {1 \over \tan \theta }}
cot
θ
{\displaystyle \cot \theta \ }
1
sec
2
θ
−
1
{\displaystyle {1 \over {\sqrt {\sec ^{2}\theta -1}}}}
csc
2
θ
−
1
{\displaystyle {\sqrt {\csc ^{2}\theta -1}}}
sec
θ
{\displaystyle \sec \theta }
1
1
−
sin
2
θ
{\displaystyle {1 \over {\sqrt {1-\sin ^{2}\theta }}}}
1
cos
θ
{\displaystyle {1 \over \cos \theta }}
1
+
tan
2
θ
{\displaystyle {\sqrt {1+\tan ^{2}\theta }}}
1
+
cot
2
θ
cot
θ
{\displaystyle {{\sqrt {1+\cot ^{2}\theta }} \over \cot \theta }}
sec
θ
{\displaystyle \sec \theta \ }
csc
θ
csc
2
θ
−
1
{\displaystyle {\csc \theta \over {\sqrt {\csc ^{2}\theta -1}}}}
csc
θ
{\displaystyle \csc \theta }
1
sin
θ
{\displaystyle {1 \over \sin \theta }}
1
1
−
cos
2
θ
{\displaystyle {1 \over {\sqrt {1-\cos ^{2}\theta }}}}
1
+
tan
2
θ
tan
θ
{\displaystyle {{\sqrt {1+\tan ^{2}\theta }} \over \tan \theta }}
1
+
cot
2
θ
{\displaystyle {\sqrt {1+\cot ^{2}\theta }}}
sec
θ
sec
2
θ
−
1
{\displaystyle {\sec \theta \over {\sqrt {\sec ^{2}\theta -1}}}}
csc
θ
{\displaystyle \csc \theta \ }
正矢 、餘矢 、半正矢 、半餘矢 、外正割 用於航行。例如半正矢 可以計算球體上的兩個點之間的距離,但它們不常用。
名稱
函數
值[ 1]
正矢 , versine
versin
θ
{\displaystyle \operatorname {versin} \theta }
vers
θ
{\displaystyle \operatorname {vers} \theta }
ver
θ
{\displaystyle \operatorname {ver} \theta }
1
−
cos
θ
{\displaystyle 1-\cos \theta }
餘的正矢 , vercosine
vercosin
θ
{\displaystyle \operatorname {vercosin} \theta }
1
+
cos
θ
{\displaystyle 1+\cos \theta }
餘矢 , coversine
coversin
θ
{\displaystyle \operatorname {coversin} \theta }
cvs
θ
{\displaystyle \operatorname {cvs} \theta }
1
−
sin
θ
{\displaystyle 1-\sin \theta }
餘的餘矢 , covercosine
covercosin
θ
{\displaystyle \operatorname {covercosin} \theta }
1
+
sin
θ
{\displaystyle 1+\sin \theta }
半正矢 , haversine
haversin
θ
{\displaystyle \operatorname {haversin} \theta }
1
−
cos
θ
2
{\displaystyle {\frac {1-\cos \theta }{2}}}
餘的半正矢 , havercosine
havercosin
θ
{\displaystyle \operatorname {havercosin} \theta }
1
+
cos
θ
2
{\displaystyle {\frac {1+\cos \theta }{2}}}
半餘矢 , hacoversine
hacoversin
θ
{\displaystyle \operatorname {hacoversin} \theta }
1
−
sin
θ
2
{\displaystyle {\frac {1-\sin \theta }{2}}}
餘的半餘矢 , hacovercosine
hacovercosin
θ
{\displaystyle \operatorname {hacovercosin} \theta }
1
+
sin
θ
2
{\displaystyle {\frac {1+\sin \theta }{2}}}
外正割 ,exsecant
exsec
θ
{\displaystyle \operatorname {exsec} \theta }
sec
θ
−
1
{\displaystyle \sec \theta -1}
外餘割 ,excosecant
excsc
θ
{\displaystyle \operatorname {excsc} \theta }
csc
θ
−
1
{\displaystyle \csc \theta -1}
弦函數 , chord
crd
θ
{\displaystyle \operatorname {crd} \theta }
2
sin
(
θ
2
)
{\displaystyle 2\sin \left({\frac {\theta }{2}}\right)}
純虛數指數函數 ,
cis
θ
{\displaystyle \operatorname {cis} \theta }
cos
θ
+
i
sin
θ
{\displaystyle \cos \theta +i\;\sin \theta }
輻角 ,Argument
arg
x
{\displaystyle \arg x}
Im
(
ln
x
)
{\displaystyle \operatorname {Im} (\ln x)}
通過檢視單位圓 ,可確立三角函數的下列性質,這些性質也被稱為誘導公式 :
當三角函数反射自某个特定的
θ
{\displaystyle \theta }
反射於
θ
=
0
{\displaystyle \theta =0}
反射於
θ
=
π
4
{\displaystyle \theta ={\tfrac {\pi }{4}}}
反射於
θ
=
π
2
{\displaystyle \theta ={\tfrac {\pi }{2}}}
反射於
θ
=
3
π
4
{\displaystyle \theta ={\tfrac {3\pi }{4}}}
sin
(
0
−
θ
)
=
−
sin
θ
cos
(
0
−
θ
)
=
+
cos
θ
tan
(
0
−
θ
)
=
−
tan
θ
cot
(
0
−
θ
)
=
−
cot
θ
sec
(
0
−
θ
)
=
+
sec
θ
csc
(
0
−
θ
)
=
−
csc
θ
{\displaystyle {\begin{aligned}\sin(0-\theta )&=-\sin \theta \\\cos(0-\theta )&=+\cos \theta \\\tan(0-\theta )&=-\tan \theta \\\cot(0-\theta )&=-\cot \theta \\\sec(0-\theta )&=+\sec \theta \\\csc(0-\theta )&=-\csc \theta \end{aligned}}}
sin
(
π
2
−
θ
)
=
+
cos
θ
cos
(
π
2
−
θ
)
=
+
sin
θ
tan
(
π
2
−
θ
)
=
+
cot
θ
cot
(
π
2
−
θ
)
=
+
tan
θ
sec
(
π
2
−
θ
)
=
+
csc
θ
csc
(
π
2
−
θ
)
=
+
sec
θ
{\displaystyle {\begin{aligned}\sin({\tfrac {\pi }{2}}-\theta )&=+\cos \theta \\\cos({\tfrac {\pi }{2}}-\theta )&=+\sin \theta \\\tan({\tfrac {\pi }{2}}-\theta )&=+\cot \theta \\\cot({\tfrac {\pi }{2}}-\theta )&=+\tan \theta \\\sec({\tfrac {\pi }{2}}-\theta )&=+\csc \theta \\\csc({\tfrac {\pi }{2}}-\theta )&=+\sec \theta \end{aligned}}}
sin
(
π
−
θ
)
=
+
sin
θ
cos
(
π
−
θ
)
=
−
cos
θ
tan
(
π
−
θ
)
=
−
tan
θ
cot
(
π
−
θ
)
=
−
cot
θ
sec
(
π
−
θ
)
=
−
sec
θ
csc
(
π
−
θ
)
=
+
csc
θ
{\displaystyle {\begin{aligned}\sin(\pi -\theta )&=+\sin \theta \\\cos(\pi -\theta )&=-\cos \theta \\\tan(\pi -\theta )&=-\tan \theta \\\cot(\pi -\theta )&=-\cot \theta \\\sec(\pi -\theta )&=-\sec \theta \\\csc(\pi -\theta )&=+\csc \theta \end{aligned}}}
sin
(
3
π
2
−
θ
)
=
−
cos
θ
cos
(
3
π
2
−
θ
)
=
−
sin
θ
tan
(
3
π
2
−
θ
)
=
+
cot
θ
cot
(
3
π
2
−
θ
)
=
+
tan
θ
sec
(
3
π
2
−
θ
)
=
−
csc
θ
csc
(
3
π
2
−
θ
)
=
−
sec
θ
{\displaystyle {\begin{aligned}\sin({\tfrac {3\pi }{2}}-\theta )&=-\cos \theta \\\cos({\tfrac {3\pi }{2}}-\theta )&=-\sin \theta \\\tan({\tfrac {3\pi }{2}}-\theta )&=+\cot \theta \\\cot({\tfrac {3\pi }{2}}-\theta )&=+\tan \theta \\\sec({\tfrac {3\pi }{2}}-\theta )&=-\csc \theta \\\csc({\tfrac {3\pi }{2}}-\theta )&=-\sec \theta \end{aligned}}}
通過旋轉特定角度移位三角函數,經常可以找到更簡單的表達结果的不同的三角函數。例如通過旋轉
π
2
{\displaystyle {\tfrac {\pi }{2}}}
π
{\displaystyle \pi }
2
π
{\displaystyle 2\pi }
π
{\displaystyle \pi }
2
π
{\displaystyle 2\pi }
移位
π
2
{\displaystyle {\tfrac {\pi }{2}}}
移位
π
{\displaystyle \pi }
移位
3
π
2
{\displaystyle {\tfrac {3\pi }{2}}}
移位
2
π
{\displaystyle 2\pi }
tan
{\displaystyle \tan }
cot
{\displaystyle \cot }
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
csc
{\displaystyle \csc }
sec
{\displaystyle \sec }
sin
(
θ
+
π
2
)
=
+
cos
θ
cos
(
θ
+
π
2
)
=
−
sin
θ
tan
(
θ
+
π
2
)
=
−
cot
θ
cot
(
θ
+
π
2
)
=
−
tan
θ
sec
(
θ
+
π
2
)
=
−
csc
θ
csc
(
θ
+
π
2
)
=
+
sec
θ
{\displaystyle {\begin{aligned}\sin(\theta +{\tfrac {\pi }{2}})&=+\cos \theta \\\cos(\theta +{\tfrac {\pi }{2}})&=-\sin \theta \\\tan(\theta +{\tfrac {\pi }{2}})&=-\cot \theta \\\cot(\theta +{\tfrac {\pi }{2}})&=-\tan \theta \\\sec(\theta +{\tfrac {\pi }{2}})&=-\csc \theta \\\csc(\theta +{\tfrac {\pi }{2}})&=+\sec \theta \end{aligned}}}
sin
(
θ
+
π
)
=
−
sin
θ
cos
(
θ
+
π
)
=
−
cos
θ
tan
(
θ
+
π
)
=
+
tan
θ
cot
(
θ
+
π
)
=
+
cot
θ
sec
(
θ
+
π
)
=
−
sec
θ
csc
(
θ
+
π
)
=
−
csc
θ
{\displaystyle {\begin{aligned}\sin(\theta +\pi )&=-\sin \theta \\\cos(\theta +\pi )&=-\cos \theta \\\tan(\theta +\pi )&=+\tan \theta \\\cot(\theta +\pi )&=+\cot \theta \\\sec(\theta +\pi )&=-\sec \theta \\\csc(\theta +\pi )&=-\csc \theta \end{aligned}}}
sin
(
θ
+
3
π
2
)
=
−
cos
θ
cos
(
θ
+
3
π
2
)
=
+
sin
θ
tan
(
θ
+
3
π
2
)
=
−
cot
θ
cot
(
θ
+
3
π
2
)
=
−
tan
θ
sec
(
θ
+
3
π
2
)
=
+
csc
θ
csc
(
θ
+
3
π
2
)
=
−
sec
θ
{\displaystyle {\begin{aligned}\sin(\theta +{\tfrac {3\pi }{2}})&=-\cos \theta \\\cos(\theta +{\tfrac {3\pi }{2}})&=+\sin \theta \\\tan(\theta +{\tfrac {3\pi }{2}})&=-\cot \theta \\\cot(\theta +{\tfrac {3\pi }{2}})&=-\tan \theta \\\sec(\theta +{\tfrac {3\pi }{2}})&=+\csc \theta \\\csc(\theta +{\tfrac {3\pi }{2}})&=-\sec \theta \end{aligned}}}
sin
(
θ
+
2
π
)
=
+
sin
θ
cos
(
θ
+
2
π
)
=
+
cos
θ
tan
(
θ
+
2
π
)
=
+
tan
θ
cot
(
θ
+
2
π
)
=
+
cot
θ
sec
(
θ
+
2
π
)
=
+
sec
θ
csc
(
θ
+
2
π
)
=
+
csc
θ
{\displaystyle {\begin{aligned}\sin(\theta +2\pi )&=+\sin \theta \\\cos(\theta +2\pi )&=+\cos \theta \\\tan(\theta +2\pi )&=+\tan \theta \\\cot(\theta +2\pi )&=+\cot \theta \\\sec(\theta +2\pi )&=+\sec \theta \\\csc(\theta +2\pi )&=+\csc \theta \end{aligned}}}
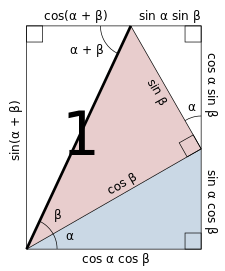
正弦與餘弦的角和公式的圖形證明法。使用了相似三角形的性質與三角函數的定義,強調的線段是單位長度 正切的角和公式的圖形證明法。使用了相似三角形的性質與三角函數的定義,強調的線段是單位長度。 又稱做“和差定理”、“和差公式”或“和角公式”。最簡要的檢定方式是使用歐拉公式 [ 註 1]
根据
s
i
n
π
4
=
c
o
s
π
4
=
1
2
{\displaystyle sin{\frac {\pi }{4}}=cos{\frac {\pi }{4}}={\frac {1}{\sqrt {2}}}}
sin
α
+
cos
α
=
2
(
sin
α
cos
π
4
+
sin
π
4
cos
α
)
=
2
sin
(
α
+
π
4
)
=
2
cos
(
α
−
π
4
)
{\displaystyle \sin \alpha +\cos \alpha ={\sqrt {2}}\left(\sin \alpha \cos {\frac {\pi }{4}}+\sin {\frac {\pi }{4}}\cos \alpha \right)={\sqrt {2}}\sin \left(\alpha +{\frac {\pi }{4}}\right)={\sqrt {2}}\cos \left(\alpha -{\frac {\pi }{4}}\right)}
sin
α
−
cos
α
=
2
(
sin
α
cos
π
4
−
sin
π
4
cos
α
)
=
2
sin
(
α
−
π
4
)
=
2
cos
(
α
+
π
4
)
{\displaystyle \sin \alpha -\cos \alpha ={\sqrt {2}}\left(\sin \alpha \cos {\frac {\pi }{4}}-\sin {\frac {\pi }{4}}\cos \alpha \right)={\sqrt {2}}\sin \left(\alpha -{\frac {\pi }{4}}\right)={\sqrt {2}}\cos \left(\alpha +{\frac {\pi }{4}}\right)}
sin
(
∑
i
=
1
∞
θ
i
)
=
∑
o
d
d
k
≥
1
(
−
1
)
k
−
1
2
∑
|
A
|
=
k
(
∏
i
∈
A
sin
θ
i
∏
i
∉
A
cos
θ
i
)
{\displaystyle \sin \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{\mathrm {odd} \ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{|A|=k}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)}
cos
(
∑
i
=
1
∞
θ
i
)
=
∑
e
v
e
n
k
≥
0
(
−
1
)
k
2
∑
|
A
|
=
k
(
∏
i
∈
A
sin
θ
i
∏
i
∉
A
cos
θ
i
)
{\displaystyle \cos \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{\mathrm {even} \ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{|A|=k}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)}
這里的"
|
A
|
=
k
{\displaystyle |A|=k}
A
{\displaystyle A}
{
1
,
2
,
3
,
…
}
{\displaystyle \left\{1,2,3,\ldots \right\}}
k
{\displaystyle k}
在这两个恒等式中出现了在有限多项中不出现的不对称:在每个乘积中,只有有限多个正弦因子和餘有限 多个余弦因子。
如果只有有限多项
θ
i
{\displaystyle \theta _{i}}
设
x
i
=
tan
θ
i
{\displaystyle x_{i}=\tan \theta _{i}}
i
=
1
,
…
,
n
{\displaystyle i=1,\ldots ,n}
e
k
{\displaystyle e_{k}}
x
i
{\displaystyle x_{i}}
i
=
1
,
…
,
n
{\displaystyle i=1,\ldots ,n}
k
=
0
,
…
,
n
{\displaystyle k=0,\ldots ,n}
k
{\displaystyle k}
基本对称多项式 。则
tan
(
θ
1
+
⋯
+
θ
n
)
=
e
1
−
e
3
+
e
5
−
⋯
e
0
−
e
2
+
e
4
−
⋯
,
{\displaystyle \tan(\theta _{1}+\cdots +\theta _{n})={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }},}
项的数目依赖于
n
{\displaystyle n}
tan
(
θ
1
+
θ
2
+
θ
3
)
=
e
1
−
e
3
e
0
−
e
2
=
(
x
1
+
x
2
+
x
3
)
−
(
x
1
x
2
x
3
)
1
−
(
x
1
x
2
+
x
1
x
3
+
x
2
x
3
)
,
tan
(
θ
1
+
θ
2
+
θ
3
+
θ
4
)
=
e
1
−
e
3
e
0
−
e
2
+
e
4
=
(
x
1
+
x
2
+
x
3
+
x
4
)
−
(
x
1
x
2
x
3
+
x
1
x
2
x
4
+
x
1
x
3
x
4
+
x
2
x
3
x
4
)
1
−
(
x
1
x
2
+
x
1
x
3
+
x
1
x
4
+
x
2
x
3
+
x
2
x
4
+
x
3
x
4
)
+
(
x
1
x
2
x
3
x
4
)
,
{\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2}+\theta _{3})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\\\\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\\\&{}={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}
并以此类推。一般情况可通过数学归纳法 证明。
T
n
{\displaystyle T_{n}}
n
{\displaystyle n}
切比雪夫多项式
cos
n
θ
=
T
n
cos
θ
{\displaystyle \cos n\theta =T_{n}\cos \theta \,}
S
n
{\displaystyle S_{n}}
n
{\displaystyle n}
伸展多项式
sin
2
n
θ
=
S
n
sin
2
θ
{\displaystyle \sin ^{2}n\theta =S_{n}\sin ^{2}\theta \,}
棣莫弗定理 ,
i
{\displaystyle i}
虚单位
cos
n
θ
+
i
sin
n
θ
=
(
cos
θ
+
i
sin
θ
)
n
{\displaystyle \cos n\theta +i\sin n\theta =(\cos \theta +i\sin \theta )^{n}\,}
1
+
2
cos
x
+
2
cos
2
x
+
2
cos
3
x
+
⋯
+
2
cos
(
n
x
)
=
sin
[
(
n
+
1
2
)
x
]
sin
x
2
{\displaystyle 1+2\cos x+2\cos 2x+2\cos 3x+\cdots +2\cos(nx)={\frac {\sin \left[\left(n+{\frac {1}{2}}\right)x\right]}{\sin {\frac {x}{2}}}}}
(這個
x
{\displaystyle x}
狄利克雷核 。)
這些公式可以使用和差恒等式或多倍角公式来证明。
弦
切
割
雙倍角公式 正
sin
2
θ
=
2
sin
θ
cos
θ
=
2
tan
θ
1
+
tan
2
θ
{\displaystyle {\begin{aligned}\sin 2\theta &=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}}
tan
2
θ
=
2
tan
θ
1
−
tan
2
θ
=
1
1
−
tan
θ
−
1
1
+
tan
θ
{\displaystyle {\begin{aligned}\tan 2\theta &={\frac {2\tan \theta }{1-\tan ^{2}\theta }}\ \\&={\frac {1}{1-\tan \theta }}-{\frac {1}{1+\tan \theta }}\end{aligned}}}
sec
2
θ
=
sec
2
θ
1
−
tan
2
θ
=
sec
2
θ
2
−
sec
2
θ
{\displaystyle {\begin{aligned}\sec 2\theta &={\frac {\sec ^{2}\theta }{1-\tan ^{2}\theta }}\\&={\frac {\sec ^{2}\theta }{2-\sec ^{2}\theta }}\end{aligned}}}
餘
cos
2
θ
=
cos
2
θ
−
sin
2
θ
=
2
cos
2
θ
−
1
=
1
−
2
sin
2
θ
=
1
−
tan
2
θ
1
+
tan
2
θ
{\displaystyle {\begin{aligned}\cos 2\theta &=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}}
cot
2
θ
=
cot
2
θ
−
1
2
cot
θ
=
cot
θ
−
tan
θ
2
{\displaystyle {\begin{aligned}\cot 2\theta &={\frac {\cot ^{2}\theta -1}{2\cot \theta }}\\&={\frac {\cot \theta -\tan \theta }{2}}\end{aligned}}}
csc
2
θ
=
csc
2
θ
2
cot
θ
=
sec
θ
csc
θ
2
{\displaystyle {\begin{aligned}\csc 2\theta &={\frac {\csc ^{2}\theta }{2\cot \theta }}\\&={\frac {\sec \theta \csc \theta }{2}}\end{aligned}}}
降次公式
正
sin
2
θ
=
1
−
cos
2
θ
2
{\displaystyle \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}}
tan
2
θ
=
1
−
cos
2
θ
1
+
cos
2
θ
{\displaystyle \tan ^{2}\theta ={\frac {1-\cos 2\theta }{1+\cos 2\theta }}}
餘
cos
2
θ
=
1
+
cos
2
θ
2
{\displaystyle \cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}}
cot
2
θ
=
1
+
cos
2
θ
1
−
cos
2
θ
{\displaystyle \cot ^{2}\theta ={\frac {1+\cos 2\theta }{1-\cos 2\theta }}}
三倍角公式 正
sin
3
θ
=
3
sin
θ
−
4
sin
3
θ
=
4
sin
θ
sin
(
π
3
−
θ
)
sin
(
π
3
+
θ
)
{\displaystyle {\begin{aligned}\sin 3\theta &=3\sin \theta -4\sin ^{3}\theta \\&=4\sin \theta \sin \left({\frac {\pi }{3}}-\theta \right)\sin \left({\frac {\pi }{3}}+\theta \right)\end{aligned}}}
tan
3
θ
=
3
tan
θ
−
tan
3
θ
1
−
3
tan
2
θ
=
tan
θ
tan
(
π
3
−
θ
)
tan
(
π
3
+
θ
)
{\displaystyle {\begin{aligned}\tan 3\theta &={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}\\&=\tan \theta \tan \left({\frac {\pi }{3}}-\theta \right)\tan \left({\frac {\pi }{3}}+\theta \right)\end{aligned}}}
sec
3
θ
=
sec
3
θ
4
−
3
sec
2
θ
=
1
4
cos
θ
cos
(
π
3
−
θ
)
cos
(
π
3
+
θ
)
{\displaystyle {\begin{aligned}\sec 3\theta &={\frac {\sec ^{3}\theta }{4-3\sec ^{2}\theta }}\\&={\dfrac {1}{4\cos \theta \cos \left({\dfrac {\pi }{3}}-\theta \right)\cos \left({\dfrac {\pi }{3}}+\theta \right)}}\end{aligned}}}
餘
cos
3
θ
=
4
cos
3
θ
−
3
cos
θ
=
4
cos
θ
cos
(
π
3
−
θ
)
cos
(
π
3
+
θ
)
{\displaystyle {\begin{aligned}\cos 3\theta &=4\cos ^{3}\theta -3\cos \theta \\&=4\cos \theta \cos \left({\frac {\pi }{3}}-\theta \right)\cos \left({\frac {\pi }{3}}+\theta \right)\end{aligned}}}
cot
3
θ
=
cot
3
θ
−
3
cot
θ
3
cot
2
θ
−
1
=
cot
θ
cot
(
π
3
−
θ
)
cot
(
π
3
+
θ
)
{\displaystyle {\begin{aligned}\cot 3\theta &={\frac {\cot ^{3}\theta -3\cot \theta }{3\cot ^{2}\theta -1}}\\&=\cot \theta \cot \left({\frac {\pi }{3}}-\theta \right)\cot \left({\frac {\pi }{3}}+\theta \right)\end{aligned}}}
csc
3
θ
=
csc
3
θ
3
csc
2
θ
−
4
=
1
4
sin
θ
sin
(
π
3
−
θ
)
sin
(
π
3
+
θ
)
{\displaystyle {\begin{aligned}\csc 3\theta &={\frac {\csc ^{3}\theta }{3\csc ^{2}\theta -4}}\\&={\dfrac {1}{4\sin \theta \sin \left({\dfrac {\pi }{3}}-\theta \right)\sin \left({\dfrac {\pi }{3}}+\theta \right)}}\end{aligned}}}
半角公式 正
sin
θ
2
=
±
1
−
cos
θ
2
{\displaystyle \sin {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}}
tan
θ
2
=
csc
θ
−
cot
θ
=
±
1
−
cos
θ
1
+
cos
θ
=
sin
θ
1
+
cos
θ
=
1
−
cos
θ
sin
θ
=
cos
θ
+
sin
θ
−
1
cos
θ
−
sin
θ
+
1
=
cot
2
θ
+
1
−
cot
θ
{\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {1-\cos \theta \over 1+\cos \theta }}\\&={\frac {\sin \theta }{1+\cos \theta }}\\&={\frac {1-\cos \theta }{\sin \theta }}\\&={\frac {\cos \theta +\sin \theta -1}{\cos \theta -\sin \theta +1}}\\&={\sqrt {\cot ^{2}\theta +1}}-\cot \theta \end{aligned}}}
sec
θ
2
=
±
2
sec
θ
sec
θ
+
1
{\displaystyle \sec {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {2\sec \theta }{\sec \theta +1}}}}
餘
cos
θ
2
=
±
1
+
cos
θ
2
{\displaystyle \cos {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}}}
cot
θ
2
=
csc
θ
+
cot
θ
=
±
1
+
cos
θ
1
−
cos
θ
=
sin
θ
1
−
cos
θ
=
1
+
cos
θ
sin
θ
=
cos
θ
−
sin
θ
+
1
cos
θ
+
sin
θ
−
1
=
cot
2
θ
+
1
+
cot
θ
{\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {1+\cos \theta \over 1-\cos \theta }}\\&={\frac {\sin \theta }{1-\cos \theta }}\\&={\frac {1+\cos \theta }{\sin \theta }}\\&={\frac {\cos \theta -\sin \theta +1}{\cos \theta +\sin \theta -1}}\\&={\sqrt {\cot ^{2}\theta +1}}+\cot \theta \end{aligned}}}
csc
θ
2
=
±
2
sec
θ
sec
θ
−
1
{\displaystyle \csc {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {2\sec \theta }{\sec \theta -1}}}}
参见正切半角公式 ,它也叫做“万能公式”。
正矢
versin
2
θ
=
2
sin
2
θ
=
(
sin
2
θ
)
(
sin
θ
)
cos
θ
=
1
−
cos
2
θ
{\displaystyle \operatorname {versin} 2\theta =2\sin ^{2}\theta ={\frac {(\sin 2\theta )(\sin \theta )}{\cos \theta }}=1-\cos 2\theta }
餘矢
cvs
2
θ
=
(
sin
θ
−
cos
θ
)
2
=
1
−
sin
2
θ
{\displaystyle \operatorname {cvs} 2\theta =(\sin \theta -\cos \theta )^{2}=1-\sin 2\theta }
从解余弦二倍角公式的第二和第三版本得到。
正弦
餘弦
其他
sin
2
θ
=
1
−
cos
2
θ
2
{\displaystyle \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}}
cos
2
θ
=
1
+
cos
2
θ
2
{\displaystyle \cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}}
sin
2
θ
cos
2
θ
=
1
−
cos
4
θ
8
{\displaystyle \sin ^{2}\theta \cos ^{2}\theta ={\frac {1-\cos 4\theta }{8}}}
sin
3
θ
=
3
sin
θ
−
sin
3
θ
4
{\displaystyle \sin ^{3}\theta ={\frac {3\sin \theta -\sin 3\theta }{4}}}
cos
3
θ
=
3
cos
θ
+
cos
3
θ
4
{\displaystyle \cos ^{3}\theta ={\frac {3\cos \theta +\cos 3\theta }{4}}}
sin
3
θ
cos
3
θ
=
3
sin
2
θ
−
sin
6
θ
32
{\displaystyle \sin ^{3}\theta \cos ^{3}\theta ={\frac {3\sin 2\theta -\sin 6\theta }{32}}}
sin
4
θ
=
3
−
4
cos
2
θ
+
cos
4
θ
8
{\displaystyle \sin ^{4}\theta ={\frac {3-4\cos 2\theta +\cos 4\theta }{8}}}
cos
4
θ
=
3
+
4
cos
2
θ
+
cos
4
θ
8
{\displaystyle \cos ^{4}\theta ={\frac {3+4\cos 2\theta +\cos 4\theta }{8}}}
sin
4
θ
cos
4
θ
=
3
−
4
cos
4
θ
+
cos
8
θ
128
{\displaystyle \sin ^{4}\theta \cos ^{4}\theta ={\frac {3-4\cos 4\theta +\cos 8\theta }{128}}}
sin
5
θ
=
10
sin
θ
−
5
sin
3
θ
+
sin
5
θ
16
{\displaystyle \sin ^{5}\theta ={\frac {10\sin \theta -5\sin 3\theta +\sin 5\theta }{16}}}
cos
5
θ
=
10
cos
θ
+
5
cos
3
θ
+
cos
5
θ
16
{\displaystyle \cos ^{5}\theta ={\frac {10\cos \theta +5\cos 3\theta +\cos 5\theta }{16}}}
sin
5
θ
cos
5
θ
=
10
sin
2
θ
−
5
sin
6
θ
+
sin
10
θ
512
{\displaystyle \sin ^{5}\theta \cos ^{5}\theta ={\frac {10\sin 2\theta -5\sin 6\theta +\sin 10\theta }{512}}}
餘弦
正弦
如果
n
{\displaystyle n}
奇數
cos
n
θ
=
2
2
n
∑
k
=
0
n
−
1
2
(
n
k
)
cos
[
(
n
−
2
k
)
θ
]
{\displaystyle \cos ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {[(n-2k)\theta ]}}
sin
n
θ
=
2
2
n
∑
k
=
0
n
−
1
2
(
−
1
)
(
n
−
1
2
−
k
)
(
n
k
)
sin
[
(
n
−
2
k
)
θ
]
{\displaystyle \sin ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{\left({\frac {n-1}{2}}-k\right)}{\binom {n}{k}}\sin {[(n-2k)\theta ]}}
如果
n
{\displaystyle n}
偶數
cos
n
θ
=
1
2
n
(
n
n
2
)
+
2
2
n
∑
k
=
0
n
2
−
1
(
n
k
)
cos
[
(
n
−
2
k
)
θ
]
{\displaystyle \cos ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {[(n-2k)\theta ]}}
sin
n
θ
=
1
2
n
(
n
n
2
)
+
2
2
n
∑
k
=
0
n
2
−
1
(
−
1
)
(
n
2
−
k
)
(
n
k
)
cos
[
(
n
−
2
k
)
θ
]
{\displaystyle \sin ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{\left({\frac {n}{2}}-k\right)}{\binom {n}{k}}\cos {[(n-2k)\theta ]}}
∏
k
=
0
n
−
1
cos
2
k
θ
=
sin
2
n
θ
2
n
sin
θ
{\displaystyle \prod _{k=0}^{n-1}\cos 2^{k}\theta ={\frac {\sin 2^{n}\theta }{2^{n}\sin \theta }}}
[ 2]
∏
k
=
0
n
−
1
sin
(
x
+
k
π
n
)
=
sin
n
x
2
n
−
1
{\displaystyle \prod _{k=0}^{n-1}\sin \left(x+{\frac {k\pi }{n}}\right)={\frac {\sin nx}{2^{n-1}}}}
[ 2]
∏
k
=
1
n
−
1
sin
(
k
π
n
)
=
n
2
n
−
1
{\displaystyle \prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{n}}\right)={\frac {n}{2^{n-1}}}}
∏
k
=
1
n
−
1
sin
(
k
π
2
n
)
=
n
2
n
−
1
{\displaystyle \prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{2n}}\right)={\frac {\sqrt {n}}{2^{n-1}}}}
∏
k
=
1
n
sin
(
k
π
2
n
+
1
)
=
2
n
+
1
2
n
{\displaystyle \prod _{k=1}^{n}\sin \left({\frac {k\pi }{2n+1}}\right)={\frac {\sqrt {2n+1}}{2^{n}}}}
∏
k
=
1
n
−
1
cos
(
k
π
n
)
=
sin
n
π
2
2
n
−
1
{\displaystyle \prod _{k=1}^{n-1}\cos \left({\frac {k\pi }{n}}\right)={\frac {\sin {\frac {n\pi }{2}}}{2^{n-1}}}}
∏
k
=
1
n
−
1
cos
(
k
π
2
n
)
=
n
2
n
−
1
{\displaystyle \prod _{k=1}^{n-1}\cos \left({\frac {k\pi }{2n}}\right)={\frac {\sqrt {n}}{2^{n-1}}}}
∏
k
=
1
n
cos
(
k
π
2
n
+
1
)
=
1
2
n
{\displaystyle \prod _{k=1}^{n}\cos \left({\frac {k\pi }{2n+1}}\right)={\frac {1}{2^{n}}}}
∏
k
=
1
n
−
1
tan
(
k
π
n
)
=
n
sin
n
π
2
{\displaystyle \prod _{k=1}^{n-1}\tan \left({\frac {k\pi }{n}}\right)={\frac {n}{\sin {\frac {n\pi }{2}}}}}
∏
k
=
1
n
−
1
tan
(
k
π
2
n
)
=
1
{\displaystyle \prod _{k=1}^{n-1}\tan \left({\frac {k\pi }{2n}}\right)=1}
∏
k
=
1
n
tan
k
π
2
n
+
1
=
2
n
+
1
{\displaystyle \prod _{k=1}^{n}\tan {\frac {k\pi }{2n+1}}={\sqrt {2n+1}}}
數學家韋達 在其三角學著作《應用於三角形的數學定律》給出积化和差与和差化积恒等式。积化和差恒等式可以通过展开角的和差恒等式的右手端来证明。
积化和差
和差化积
sin
α
cos
β
=
sin
(
α
+
β
)
+
sin
(
α
−
β
)
2
{\displaystyle \sin \alpha \cos \beta ={\sin(\alpha +\beta )+\sin(\alpha -\beta ) \over 2}}
sin
α
+
sin
β
=
2
sin
α
+
β
2
cos
α
−
β
2
{\displaystyle \sin \alpha +\sin \beta =2\sin {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}}
cos
α
sin
β
=
sin
(
α
+
β
)
−
sin
(
α
−
β
)
2
{\displaystyle \cos \alpha \sin \beta ={\sin(\alpha +\beta )-\sin(\alpha -\beta ) \over 2}}
sin
α
−
sin
β
=
2
cos
α
+
β
2
sin
α
−
β
2
{\displaystyle \sin \alpha -\sin \beta =2\cos {\alpha +\beta \over 2}\sin {\alpha -\beta \over 2}}
cos
α
cos
β
=
cos
(
α
+
β
)
+
cos
(
α
−
β
)
2
{\displaystyle \cos \alpha \cos \beta ={\cos(\alpha +\beta )+\cos(\alpha -\beta ) \over 2}}
cos
α
+
cos
β
=
2
cos
α
+
β
2
cos
α
−
β
2
{\displaystyle \cos \alpha +\cos \beta =2\cos {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}}
sin
α
sin
β
=
−
cos
(
α
+
β
)
−
cos
(
α
−
β
)
2
{\displaystyle \sin \alpha \sin \beta =-{\cos(\alpha +\beta )-\cos(\alpha -\beta ) \over 2}}
cos
α
−
cos
β
=
−
2
sin
α
+
β
2
sin
α
−
β
2
{\displaystyle \cos \alpha -\cos \beta =-2\sin {\alpha +\beta \over 2}\sin {\alpha -\beta \over 2}}
sin
(
x
+
y
)
sin
(
x
−
y
)
=
sin
2
x
−
sin
2
y
=
cos
2
y
−
cos
2
x
{\displaystyle \sin(x+y)\sin(x-y)=\sin ^{2}{x}-\sin ^{2}{y}=\cos ^{2}{y}-\cos ^{2}{x}\,}
cos
(
x
+
y
)
cos
(
x
−
y
)
=
cos
2
x
−
sin
2
y
=
cos
2
y
−
sin
2
x
{\displaystyle \cos(x+y)\cos(x-y)=\cos ^{2}{x}-\sin ^{2}{y}=\cos ^{2}{y}-\sin ^{2}{x}\,}
(可藉由積化和差公式+2倍角公式推導而來)
如果
x
+
y
+
z
=
n
π
{\displaystyle x+y+z=n\pi }
那么
tan
x
+
tan
y
+
tan
z
=
tan
x
tan
y
tan
z
{\displaystyle \tan x+\tan y+\tan z=\tan x\tan y\tan z}
cot
x
cot
y
+
cot
y
cot
z
+
cot
z
cot
x
=
1
{\displaystyle \cot x\cot y+\cot y\cot z+\cot z\cot x=1}
如果
x
+
y
+
z
=
n
π
+
π
2
{\displaystyle x+y+z=n\pi +{\frac {\pi }{2}}}
那么
tan
x
tan
y
+
tan
y
tan
z
+
tan
z
tan
x
=
1
{\displaystyle \tan x\tan y+\tan y\tan z+\tan z\tan x=1}
cot
x
+
cot
y
+
cot
z
=
cot
x
cot
y
cot
z
{\displaystyle \cot x+\cot y+\cot z=\cot x\cot y\cot z}
如果
x
+
y
+
z
=
π
{\displaystyle x+y+z=\pi }
那么
sin
2
x
+
sin
2
y
+
sin
2
z
=
4
sin
x
sin
y
sin
z
{\displaystyle \sin 2x+\sin 2y+\sin 2z=4\sin x\sin y\sin z}
sin
x
+
sin
y
+
sin
z
=
4
cos
x
2
cos
y
2
cos
z
2
{\displaystyle \sin x+\sin y+\sin z=4\cos {\frac {x}{2}}\cos {\frac {y}{2}}\cos {\frac {z}{2}}}
cos
x
+
cos
y
+
cos
z
=
1
+
4
sin
x
2
sin
y
2
sin
z
2
{\displaystyle \cos x+\cos y+\cos z=1+4\sin {\frac {x}{2}}\sin {\frac {y}{2}}\sin {\frac {z}{2}}}
如果
w
+
x
+
y
+
z
=
π
{\displaystyle w+x+y+z=\pi }
那么:
sin
(
w
+
x
)
sin
(
x
+
y
)
=
sin
(
x
+
y
)
sin
(
y
+
z
)
=
sin
(
y
+
z
)
sin
(
z
+
w
)
=
sin
(
z
+
w
)
sin
(
w
+
x
)
=
sin
w
sin
y
+
sin
x
sin
z
{\displaystyle {\begin{aligned}\sin(w+x)\sin(x+y)&=\sin(x+y)\sin(y+z)\\&=\sin(y+z)\sin(z+w)\\&{}=\sin(z+w)\sin(w+x)\\&{}=\sin w\sin y+\sin x\sin z\end{aligned}}}
(前三个等式是一般情况;第四个是本质。)
利用三角恒等式的指數定義 和雙曲函數的指數定義 即可求出下列恆等式:
e
i
x
=
cos
x
+
i
sin
x
,
e
−
i
x
=
cos
x
−
i
sin
x
{\displaystyle e^{ix}=\cos x+i\;\sin x,\;e^{-ix}=\cos x-i\;\sin x}
e
x
=
cosh
x
+
sinh
x
,
e
−
x
=
cosh
x
−
sinh
x
{\displaystyle e^{x}=\cosh x+\sinh x\!,\;e^{-x}=\cosh x-\sinh x\!}
所以
cosh
i
x
=
1
2
(
e
i
x
+
e
−
i
x
)
=
cos
x
{\displaystyle \cosh ix={\tfrac {1}{2}}(e^{ix}+e^{-ix})=\cos x}
sinh
i
x
=
1
2
(
e
i
x
−
e
−
i
x
)
=
i
sin
x
{\displaystyle \sinh ix={\tfrac {1}{2}}(e^{ix}-e^{-ix})=i\sin x}
下表列出部分的三角函數 與雙曲函數 的恆等式 :
三角函數
雙曲函數
sin
θ
=
−
i
sinh
i
θ
{\displaystyle \sin \theta =-i\sinh {i\theta }\,}
sinh
θ
=
i
sin
(
−
i
θ
)
{\displaystyle \sinh {\theta }=i\sin {(-i\theta )}\,}
cos
θ
=
cosh
i
θ
{\displaystyle \cos {\theta }=\cosh {i\theta }\,}
cosh
θ
=
cos
(
−
i
θ
)
{\displaystyle \cosh {\theta }=\cos {(-i\theta )}\,}
tan
θ
=
−
i
tanh
i
θ
{\displaystyle \tan \theta =-i\tanh {i\theta }\,}
tanh
θ
=
i
tan
(
−
i
θ
)
{\displaystyle \tanh {\theta }=i\tan {(-i\theta )}\,}
cot
θ
=
i
coth
i
θ
{\displaystyle \cot {\theta }=i\coth {i\theta }\,}
coth
θ
=
−
i
cot
(
−
i
θ
)
{\displaystyle \coth \theta =-i\cot {(-i\theta )}\,}
sec
θ
=
sech
i
θ
{\displaystyle \sec {\theta }=\operatorname {sech} {\,i\theta }\,}
sech
θ
=
sec
(
−
i
θ
)
{\displaystyle \operatorname {sech} {\theta }=\sec {(-i\theta )}\,}
csc
θ
=
i
csch
i
θ
{\displaystyle \csc {\theta }=i\;\operatorname {csch} {\,i\theta }\,}
csch
θ
=
−
i
csc
(
−
i
θ
)
{\displaystyle \operatorname {csch} \theta =-i\csc {(-i\theta )}\,}
cosh
i
x
=
1
2
(
e
i
x
+
e
−
i
x
)
=
cos
x
{\displaystyle \cosh ix={\tfrac {1}{2}}(e^{ix}+e^{-ix})=\cos x}
sinh
i
x
=
1
2
(
e
i
x
−
e
−
i
x
)
=
i
sin
x
{\displaystyle \sinh ix={\tfrac {1}{2}}(e^{ix}-e^{-ix})=i\sin x}
cosh
(
x
+
i
y
)
=
cosh
(
x
)
cos
(
y
)
+
i
sinh
(
x
)
sin
(
y
)
{\displaystyle \cosh(x+iy)=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\,}
sinh
(
x
+
i
y
)
=
sinh
(
x
)
cos
(
y
)
+
i
cosh
(
x
)
sin
(
y
)
{\displaystyle \sinh(x+iy)=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\,}
tanh
i
x
=
i
tan
x
{\displaystyle \tanh ix=i\tan x\,}
cosh
x
=
cos
i
x
{\displaystyle \cosh x=\cos ix\,}
sinh
x
=
−
i
sin
i
x
{\displaystyle \sinh x=-i\sin ix\,}
tanh
x
=
−
i
tan
i
x
{\displaystyle \tanh x=-i\tan ix\,}
对于某些用途,知道同样周期但不同相位移动 的正弦波的任何线性组合 是有相同周期但不同相位移动的正弦波是重要的。在正弦和余弦波的线性组合的情况下,我们有
a
sin
x
+
b
cos
x
=
a
2
+
b
2
⋅
sin
(
x
+
φ
)
(
a
>
0
)
{\displaystyle a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\cdot \sin(x+\varphi )\;(a>0)}
这里的
φ
=
arctan
(
b
a
)
{\displaystyle \varphi =\arctan \left({\frac {b}{a}}\right)}
这个公式也叫辅助角公式或李善兰 公式。更一般的说,对于任何相位移动,我们有
a
sin
x
+
b
sin
(
x
+
α
)
=
c
sin
(
x
+
β
)
(
a
+
b
cos
x
>
0
)
{\displaystyle a\sin x+b\sin(x+\alpha )=c\sin(x+\beta )\;(a+b\cos x>0)}
这里
c
=
a
2
+
b
2
+
2
a
b
cos
α
,
{\displaystyle c={\sqrt {a^{2}+b^{2}+2ab\cos \alpha }},}
而
β
=
arctan
(
b
sin
α
a
+
b
cos
α
)
{\displaystyle \beta =\arctan \left({\frac {b\sin \alpha }{a+b\cos \alpha }}\right)}
arcsin
x
+
arccos
x
=
π
2
{\displaystyle \arcsin x+\arccos x={\frac {\pi }{2}}\;}
arctan
x
+
arccot
x
=
π
2
.
{\displaystyle \arctan x+\operatorname {arccot} x={\frac {\pi }{2}}.\;}
arctan
x
+
arctan
1
x
=
{
π
2
,
if
x
>
0
−
π
2
,
if
x
<
0
{\displaystyle \arctan x+\arctan {\frac {1}{x}}=\left\{{\begin{matrix}{\frac {\pi }{2}},&{\mbox{if }}x>0\\-{\frac {\pi }{2}},&{\mbox{if }}x<0\end{matrix}}\right.}
arctan
x
+
arctan
y
=
arctan
x
+
y
1
−
x
y
+
{
π
,
if
x
,
y
>
0
−
π
,
if
x
,
y
<
0
0
,
otherwise
{\displaystyle \arctan x+\arctan y=\arctan {\frac {x+y}{1-xy}}+\left\{{\begin{matrix}\pi ,&{\mbox{if }}x,y>0\\-\pi ,&{\mbox{if }}x,y<0\\0,&{\mbox{otherwise }}\end{matrix}}\right.}
为了用于特殊函数 ,有下列三角函数無窮乘積 公式[ 3] [ 4]
正弦(藍色)、正弦的微分(橘色),其中,正弦的微分正好是餘弦。
餘弦(藍色)、餘弦的微分(橘色),其中,餘弦的微分正好是正弦的對x軸的鏡射。
在微積分 中,下面陳述的關係要求角用弧度 來度量;如果用其他方式比如角度 來這些關係會變得更加複雜。如果三角函數以幾何的方式來定義,它們的導數可以通過驗證兩個極限而找到。第一個是:
lim
x
→
0
sin
x
x
=
1
{\displaystyle \lim _{x\rightarrow 0}{\frac {\sin x}{x}}=1}
可以使用單位圓 和夾擠定理 來驗證。如果用洛必達法則 來证明這個極限,那也就用這個極限證明了正弦的导数是餘弦,並因此在應用洛必達法則中使用正弦的導數是餘弦的事實,就是邏輯謬論中的循環論證了。第二個極限是:
lim
x
→
0
cos
x
−
1
x
=
0
{\displaystyle \lim _{x\rightarrow 0}{\frac {\cos x-1}{x}}=0}
使用恆等式
tan
x
2
=
1
−
cos
x
sin
x
{\displaystyle \tan {\frac {x}{2}}=1-{\frac {\cos x}{\sin x}}}
sin
′
x
=
cos
x
{\displaystyle \sin 'x=\cos x}
cos
′
x
=
−
sin
x
{\displaystyle \cos 'x=-\sin x}
泰勒級數 來定義,則導數可以通過冪級數逐項微分得到。
d
d
x
sin
(
x
)
=
cos
(
x
)
{\displaystyle {d \over dx}\sin(x)=\cos(x)}
結果的三角函數可以使用上述恆等式和微分 規則來做微分。
d
d
x
sin
x
=
cos
x
,
d
d
x
arcsin
x
=
1
1
−
x
2
d
d
x
cos
x
=
−
sin
x
,
d
d
x
arccos
x
=
−
1
1
−
x
2
d
d
x
tan
x
=
sec
2
x
,
d
d
x
arctan
x
=
1
1
+
x
2
d
d
x
cot
x
=
−
csc
2
x
,
d
d
x
arccot
x
=
−
1
1
+
x
2
d
d
x
sec
x
=
tan
x
sec
x
,
d
d
x
arcsec
x
=
1
|
x
|
x
2
−
1
d
d
x
csc
x
=
−
csc
x
cot
x
,
d
d
x
arccsc
x
=
−
1
|
x
|
x
2
−
1
{\displaystyle {\begin{aligned}{d \over dx}\sin x&=\cos x,&{d \over dx}\arcsin x&={1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\cos x&=-\sin x,&{d \over dx}\arccos x&=-{1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\tan x&=\sec ^{2}x,&{d \over dx}\arctan x&={1 \over 1+x^{2}}\\\\{d \over dx}\cot x&=-\csc ^{2}x,&{d \over dx}\operatorname {arccot} x&=-{1 \over 1+x^{2}}\\\\{d \over dx}\sec x&=\tan x\sec x,&{d \over dx}\operatorname {arcsec} x&={1 \over |x|{\sqrt {x^{2}-1}}}\\\\{d \over dx}\csc x&=-\csc x\cot x,&{d \over dx}\operatorname {arccsc} x&=-{1 \over |x|{\sqrt {x^{2}-1}}}\end{aligned}}}
在三角函數積分表 中可以找到積分恆等式。
三角函數(正弦和餘弦)的微分是同樣兩個函數線性組合 的事實在很多數學領域包括微分方程 和傅立葉變換 中是重要的基本原理。
函数
反函数
sin
θ
=
e
i
θ
−
e
−
i
θ
2
i
{\displaystyle \sin \theta ={\frac {e^{{i}\theta }-e^{-{i}\theta }}{2{i}}}\,}
arcsin
x
=
−
i
ln
(
i
x
+
1
−
x
2
)
{\displaystyle \arcsin x=-{i}\ln \left({i}x+{\sqrt {1-x^{2}}}\right)\,}
cos
θ
=
e
i
θ
+
e
−
i
θ
2
{\displaystyle \cos \theta ={\frac {e^{{i}\theta }+e^{-{i}\theta }}{2}}\,}
arccos
x
=
−
i
ln
(
x
+
x
2
−
1
)
{\displaystyle \arccos x=-{i}\ln \left(x+{\sqrt {x^{2}-1}}\right)\,}
tan
θ
=
e
i
θ
−
e
−
i
θ
i
(
e
i
θ
+
e
−
i
θ
)
{\displaystyle \tan \theta ={\frac {e^{{i}\theta }-e^{-{i}\theta }}{{i}(e^{{i}\theta }+e^{-{i}\theta })}}\,}
arctan
x
=
i
2
ln
(
i
+
x
i
−
x
)
{\displaystyle \arctan x={\frac {i}{2}}\ln \left({\frac {{i}+x}{{i}-x}}\right)\,}
csc
θ
=
2
i
e
i
θ
−
e
−
i
θ
{\displaystyle \csc \theta ={\frac {2{i}}{e^{{i}\theta }-e^{-{i}\theta }}}\,}
arccsc
x
=
−
i
ln
(
i
x
+
1
−
1
x
2
)
{\displaystyle \operatorname {arccsc} x=-{i}\ln \left({\tfrac {i}{x}}+{\sqrt {1-{\tfrac {1}{x^{2}}}}}\right)\,}
sec
θ
=
2
e
i
θ
+
e
−
i
θ
{\displaystyle \sec \theta ={\frac {2}{e^{{i}\theta }+e^{-{i}\theta }}}\,}
arcsec
x
=
−
i
ln
(
1
x
+
1
−
i
x
2
)
{\displaystyle \operatorname {arcsec} x=-{i}\ln \left({\tfrac {1}{x}}+{\sqrt {1-{\tfrac {i}{x^{2}}}}}\right)\,}
cot
θ
=
i
(
e
i
θ
+
e
−
i
θ
)
e
i
θ
−
e
−
i
θ
{\displaystyle \cot \theta ={\frac {{i}(e^{{i}\theta }+e^{-{i}\theta })}{e^{{i}\theta }-e^{-{i}\theta }}}\,}
arccot
x
=
i
2
ln
(
i
−
x
i
+
x
)
{\displaystyle \operatorname {arccot} x={\frac {i}{2}}\ln \left({\frac {{i}-x}{{i}+x}}\right)\,}
cis
θ
=
e
i
θ
{\displaystyle \operatorname {cis} \,\theta =e^{{i}\theta }\,}
arccis
x
=
−
i
ln
x
{\displaystyle \operatorname {arccis} \,x=-{i}\ln x\,}
sinh
θ
=
e
θ
−
e
−
θ
2
{\displaystyle \sinh \theta ={\frac {e^{\theta }-e^{-\theta }}{2}}\,}
arcsinh
x
=
ln
(
x
±
x
2
+
1
)
{\displaystyle \operatorname {arcsinh} \,x=\ln \left(x\pm {\sqrt {x^{2}+1}}\right)\,}
cosh
θ
=
e
θ
+
e
−
θ
2
{\displaystyle \cosh \theta ={\frac {e^{\theta }+e^{-\theta }}{2}}\,}
arccosh
x
=
ln
(
x
±
x
2
−
1
)
=
±
ln
(
x
+
x
2
−
1
)
{\displaystyle \operatorname {arccosh} \,x=\ln \left(x\pm {\sqrt {x^{2}-1}}\right)=\pm \ln \left(x+{\sqrt {x^{2}-1}}\right)\,}
tanh
θ
=
sinh
θ
cosh
θ
=
e
θ
−
e
−
θ
e
θ
+
e
−
θ
{\displaystyle \tanh \theta ={\frac {\sinh \theta }{\cosh \theta }}={\frac {e^{\theta }-e^{-\theta }}{e^{\theta }+e^{-\theta }}}\,}
arctanh
x
=
1
2
ln
(
1
+
x
1
−
x
)
{\displaystyle \operatorname {arctanh} \,x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)\,}
^ Abramowitz and Stegun, p. 78, 4.3.147
^ 2.0 2.1 苏学孟. 求三角函数乘积的常用方法 . 中学数学教学. 1995, (6) [2014-12-27 ] . (原始内容存档 于2014-12-27). ^ Abramowitz and Stegun, p. 75, 4.3.89–90
^ Abramowitz and Stegun, p. 85, 4.5.68–69
























































































































































































![{\displaystyle 1+2\cos x+2\cos 2x+2\cos 3x+\cdots +2\cos(nx)={\frac {\sin \left[\left(n+{\frac {1}{2}}\right)x\right]}{\sin {\frac {x}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24878792536d71a9c5b5053515b405de2af551c9)























![{\displaystyle \sin n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\sin \left[{\frac {1}{2}}(n-k)\pi \right]=\sin \theta \sum _{k=0}^{\lfloor {\frac {n-1}{2}}\rfloor }(-1)^{k}{\binom {n-1-k}{k}}~(2\cos \theta )^{n-1-2k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30a3575f39e74314218d2d046b50210fc2834b8a)
![{\displaystyle \cos n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\cos \left[{\frac {1}{2}}(n-k)\pi \right]={\frac {1}{2}}\sum _{k=0}^{\lfloor {\frac {n}{2}}\rfloor }(-1)^{k}{\frac {n}{n-k}}{\binom {n-k}{k}}~(2\cos \theta )^{n-2k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aab0b9f9ec4bc519564a1720f9d1e10338c0c2f)
![{\displaystyle \tan n\theta ={\frac {\displaystyle \sum _{k=1}^{\left[{\frac {n}{2}}\right]}(-1)^{k+1}{\binom {n}{2k-1}}\tan ^{2k-1}\theta }{\displaystyle \sum _{k=1}^{\left[{\frac {n+1}{2}}\right]}(-1)^{k+1}{\binom {n}{2(k-1)}}\tan ^{2(k-1)}\theta }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03b0563027ebb58ac7816288c76ead0dc0ba445)














![{\displaystyle \cos ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {[(n-2k)\theta ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7d3151596cd1afb5389c1566d5cbe8c51523ab3)
![{\displaystyle \sin ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{\left({\frac {n-1}{2}}-k\right)}{\binom {n}{k}}\sin {[(n-2k)\theta ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71aeee70c9d36436ed2293c9d10d931ac3bf1635)
![{\displaystyle \cos ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {[(n-2k)\theta ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313e388dfc8ef99160a6f1f04286f107bc96aa1d)
![{\displaystyle \sin ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{\left({\frac {n}{2}}-k\right)}{\binom {n}{k}}\cos {[(n-2k)\theta ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/450f6c0089bc8c2f424338bfd77e2efddf1f2cef)











































































![{\displaystyle |\sin x|={\frac {1}{2}}\prod _{n=0}^{\infty }{\sqrt[{2^{n+1}}]{\left|\tan \left(2^{n}x\right)\right|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71abcbf6e9d8704e6030ef84b53d6de4a37681ce)



























