дёүи§’еҮҪж•°зәҝжҳҜжӯЈејҰзәҝгҖҒдҪҷејҰзәҝе’ҢжӯЈеҲҮзәҝзҡ„жҖ»з§°пјҢжҳҜдёүи§’еҮҪж•°зҡ„еҮ дҪ•иЎЁзӨәгҖӮ
![]() дёүи§’еҮҪж•°зәҝпјҢи§’Оұзҡ„жүҖжңүдёүи§’еҮҪж•°еңЁеҮ дҪ•дёҠеҸҜд»ҘдҫқжҚ®д»ҘOзӮ№дёәеңҶеҝғзҡ„еҚ•дҪҚеңҶжқҘжһ„йҖ гҖӮ
дёүи§’еҮҪж•°зәҝпјҢи§’Оұзҡ„жүҖжңүдёүи§’еҮҪж•°еңЁеҮ дҪ•дёҠеҸҜд»ҘдҫқжҚ®д»ҘOзӮ№дёәеңҶеҝғзҡ„еҚ•дҪҚеңҶжқҘжһ„йҖ гҖӮ
з”ұдәҺ пјҢ
пјҢ дёҺзӮ№PпјҲx, yпјүеңЁз»Ҳиҫ№дёҠзҡ„дҪҚзҪ®ж— е…іпјҢдёәз®ҖеҚ•иө·и§ҒпјҢйҖүеҸ–и§’Оұзҡ„з»Ҳиҫ№ дёҺеҚ•дҪҚеңҶзҡ„дәӨзӮ№дёәPпјҲx, yпјүпјҢеҲҷsin Оұ = y, cos Оұ = xгҖӮ
дёҺзӮ№PпјҲx, yпјүеңЁз»Ҳиҫ№дёҠзҡ„дҪҚзҪ®ж— е…іпјҢдёәз®ҖеҚ•иө·и§ҒпјҢйҖүеҸ–и§’Оұзҡ„з»Ҳиҫ№ дёҺеҚ•дҪҚеңҶзҡ„дәӨзӮ№дёәPпјҲx, yпјүпјҢеҲҷsin Оұ = y, cos Оұ = xгҖӮ
иҝҮзӮ№PдҪңxиҪҙзҡ„еһӮзәҝпјҢеһӮи¶ідёәMпјҢжҳҫ然пјҢзәҝж®өOMзҡ„й•ҝеәҰдёә |x|пјҢдёәдәҶеҺ»жҺүз»қеҜ№еҖјз¬ҰеҸ·пјҢжҲ‘们引е…Ҙжңүеҗ‘зәҝж®өзҡ„жҰӮеҝө[1]гҖӮ
жңүеҗ‘зәҝж®ө
规е®ҡдәҶж–№еҗ‘пјҲиө·зӮ№е’Ңз»ҲзӮ№пјүзҡ„зәҝж®өз§°дёәжңүеҗ‘зәҝж®өпјҲдёҺеҗ‘йҮҸжңүеҢәеҲ«пјүпјҢзұ»дјјең°еҸҜд»ҘжҠҠ规е®ҡдәҶжӯЈж–№еҗ‘зҡ„зӣҙзәҝз§°дёәжңүеҗ‘зӣҙзәҝгҖӮиӢҘжңүеҗ‘зәҝж®өABеңЁжңүеҗ‘зӣҙзәҝlдёҠжҲ–дёҺжңүеҗ‘зӣҙзәҝlе№іиЎҢпјҢж №жҚ®жңүеҗ‘зәҝж®өABдёҺжңүеҗ‘зӣҙзәҝlзҡ„ж–№еҗ‘зӣёеҗҢжҲ–зӣёеҸҚпјҢеҲҶеҲ«жҠҠе®ғзҡ„й•ҝеәҰж·»дёҠжӯЈеҸ·жҲ–иҙҹеҸ·пјҢиҝҷж ·жүҖеҫ—зҡ„ж•°пјҢеҸ«еҒҡжңүеҗ‘зәҝж®өзҡ„ж•°йҮҸпјҢи®°дёәABгҖӮ
жӯЈејҰзәҝе’ҢдҪҷејҰзәҝ
еј•е…Ҙжңүеҗ‘зәҝж®өзҡ„жҰӮеҝөеҗҺпјҢеҰӮжһңx > 0пјҢеҰӮеӣҫпјҢжңүеҗ‘зәҝж®өOMдёҺxиҪҙеҗҢеҗ‘пјҢе…¶ж•°йҮҸдёәxпјҢеҰӮжһңx < 0пјҢжңүеҗ‘зәҝж®өOMдёҺxиҪҙеҸҚеҗ‘пјҢе…¶ж•°йҮҸд№ҹдёәxпјҢж•…жҖ»жңүOM = xгҖӮеҗҢзҗҶеҸҜзҹҘMP = y
жүҖд»ҘжңүпјҢsin Оұ = MP, cos Оұ = OM
еҚіжңүеҗ‘зәҝж®өMPгҖҒOMзҡ„ж•°йҮҸеҲҶеҲ«зӯүдәҺОұзҡ„жӯЈејҰгҖҒОұзҡ„дҪҷејҰгҖӮеӣ жӯӨпјҢжҲ‘们жҠҠжңүеҗ‘зәҝж®өMPпјҢOMеҲҶеҲ«еҸ«дҪңи§’Оұзҡ„жӯЈејҰзәҝгҖҒдҪҷејҰзәҝгҖӮ
жӯЈеҲҮзәҝ
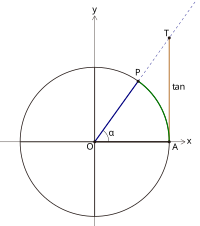
еҪ“и§’Оұзҡ„з»Ҳиҫ№еңЁyиҪҙзҡ„еҸідҫ§ж—¶пјҲеҰӮе·ҰеӣҫпјүпјҢеңЁи§’Оұзҡ„з»Ҳиҫ№дёҠеҸ–зӮ№TпјҲ1, y'пјүпјҢеҲҷ пјҲAдёәеҚ•дҪҚеңҶдёҺxиҪҙжӯЈеҚҠиҪҙзҡ„дәӨзӮ№пјү
пјҲAдёәеҚ•дҪҚеңҶдёҺxиҪҙжӯЈеҚҠиҪҙзҡ„дәӨзӮ№пјү
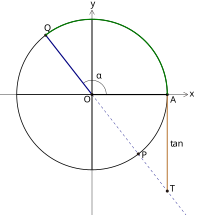
еҪ“и§’Оұз»Ҳиҫ№еңЁyиҪҙе·Ұдҫ§ж—¶пјҲеҰӮеҸіеӣҫпјүпјҢеңЁи§’Оұзҡ„з»Ҳиҫ№зҡ„еҸҚеҗ‘延й•ҝзәҝдёҠеҸ–зӮ№TпјҲ1, y'пјүз”ұдәҺе®ғе…ідәҺеҺҹзӮ№зҡ„еҜ№з§°зӮ№QпјҲвҲ’1, вҲ’y'пјүеңЁи§’Оұзҡ„з»Ҳиҫ№дёҠпјҢж•…жңү
еҚіжҖ»жңүtan Оұ = AT
еӣ жӯӨпјҢжҲ‘们жҠҠжңүеҗ‘зәҝж®өATеҸ«еҒҡи§’Оұзҡ„жӯЈеҲҮзәҝ
еҸӮиҖғиө„ж–ҷ