Giải tích toán học
|
Read other articles:

Championnats d'Europe de natation 2006 Généralités Sport Natation sportive, plongeon, nage en eau libre et natation synchronisée Organisateur(s) LEN Éditions 28e Lieu(x) Budapest, Hongrie Date 26 juillet - 6 août 2006 Nations 40 Participants 1008 Épreuves 58 Navigation Madrid 2004 Eindhoven 2008 modifier Les 28es Championnats d'Europe de natation se sont tenus à Budapest (Hongrie) du 26 juillet au 6 août 2006. La capitale hongroise accueille pour la troisième fois cet événeme...

Эту страницу предлагается объединить со страницей Фундаментальные исследования (значения).Пояснение причин и обсуждение — на странице Википедия:К объединению/13 июня 2023.Обсуждение длится не менее недели (подробнее). Не удаляйте шаблон до подведения итога обсуждения. За�...

Bachtiar Utomo Informasi pribadiLahir9 April 1960 (umur 63)Pati, Jawa TengahSuami/istriIin Nurul HudashAnakTia Indah Bhakti • Siti AstutikAlma materAkademi Militer (1984)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan DaratMasa dinas1984–2018Pangkat Mayor Jenderal TNISatuanInfanteriSunting kotak info • L • B Mayor Jenderal TNI (Purn.) Dr. Bachtiar Utomo, S.I.P., M.A.P. (lahir 9 April 1960) adalah seorang purnawirawan TNI Angkatan Darat ...
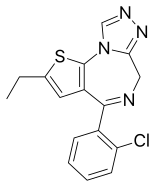
Chemical compound MetizolamClinical dataDependenceliabilityModerateRoutes ofadministrationOral, sublingual, rectalLegal statusLegal status CA: Unscheduled DE: NpSG (Industrial and scientific use only) UK: Under Psychoactive Substances Act Illegal in Sweden Identifiers IUPAC name 4-(2-Chlorophenyl)-2-ethyl-6H-thieno[3,2-f][1,2,4]triazolo[4,3-a][1,4]diazepine CAS Number40054-68-0 YPubChem CID12434325ChemSpider59207712UNIIK1C6XI9LLXChEMBLChEMBL4782672Chemical and physical dat...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Whaley Thorns – news · newspapers · books · scholar · JSTOR (August 2012) (Learn how and when to remove this template message) Human settlement in EnglandWhaley ThornsWhaley Thorns - St Lukes ChurchWhaley ThornsLocation within DerbyshireOS grid referenceSK5370Civil pa...

Scaphoid fossaSphenoid bone. Upper and posterior surfaces. (Scaphoid fossa is labeled at left.)DetailsIdentifiersLatinfossa scaphoidea ossis sphenoidalisTA98A02.1.05.047TA2633FMA84973Anatomical terms of bone[edit on Wikidata] In the pterygoid processes of the sphenoid, above the pterygoid fossa is a small, oval, shallow depression, the scaphoid fossa, which gives origin to the tensor veli palatini. It is not the same as and has to be distinguished from the scaphoid fossa of the external e...

Voce principale: Celano Football Club Marsica. Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Celano Football Club MarsicaStagione 2011-2012Sport calcio Squadra Celano Allenatore Michele Facciolo poi Attilio Tuzi poi Giuseppe Petrelli poi Michele Facciolo Presidente Ermanno Piccone Lega Pro Seconda Divisione21º posto nel gir...

Discontinued automated teller machine Tillie the All-Time TellerA screenshot of an advertisement for Tillie the All-Time TellerTypeAutomated teller machineInception1974 (1974)ManufacturerFirst National Bank of AtlantaAvailableDiscontinued Tillie the All-Time Teller was one of the first ATMs,[1] run by the First National Bank of Atlanta and considered to be one of the most successful ATMs in the banking industry. Tillie the All-Time Teller had a picture of a smiling blonde girl on...

Island in California Edgerly IslandUSGS aerial imagery of Edgerly Island. Adjacent land added since the initial survey (to top, darker) is also outlined.Edgerly IslandShow map of San Francisco Bay AreaEdgerly IslandShow map of CaliforniaEdgerly IslandShow map of the United StatesGeographyLocationNorthern CaliforniaCoordinates38°12′12″N 122°18′52″W / 38.20333°N 122.31444°W / 38.20333; -122.31444 (Edgerly Island)[1]Adjacent toNapa RiverHighest...

Kota GeorgetownKotaPemandangan kota dari Pasar StabroekJulukan: GT, The Garden City of the Caribbean, G/TownNegara GuyanaPembagian administrasiDemerara-MahaicaDidirikan1781Dinamai29 April 1812Pemerintahan • JenisWali kota-dewan • Wali kotaHamilton GreeneLuas • Luas perairan10 sq mi (30 km2) • Luas perkotaan20 sq mi (50 km2) • Luas metropolitan57 sq mi (150 km2)Ketinggian−6 ft (...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Artikel ini bukan mengenai Imperialisme ekonomi. Imperialisme ilmu ekonomi[1] dalam ilmu ekonomi kontemporer adalah analisis ekonomi terhadap aspek-aspek kehidupan yang tampaknya non-ekonomis,[2] misalnya kejahatan,[3] hukum, ...

Peta infrastruktur dan tata guna lahan di Komune Poissy. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiPoissyNegaraPrancisArondisemenSaint-Germain-en-LayeKantonIbukota 2 kantonAntarkomunebelum ada pada 2005Kode INSEE/pos78498 / Poissy merupakan sebuah komune di pinggiran barat Paris, Prancis. Terletak 23.8 km (14.8 mil) dari pusat kota Paris. Tahun 156...

American long-distance runner Anne Marie Letko (married name Lauck; born March 7, 1969, in Rochester, New York) is an American long-distance runner who competed in the Summer Olympics in 1996 (10th place in marathon) and 2000 (5000m). Anne Marie Letko is the daughter of Jim and Sandy Letko.[1] She started running at the age of 14 when she accompanied her father on jogs around the block.[2] Letko claims that she became hooked on running after winning her age division in the Ham...

此條目可参照英語維基百科相應條目来扩充。 (2021年10月13日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 国际调查记者同盟International Consortium of Investigative Journalists成立時間1997年總部华盛顿哥伦比亚特区 地址�...

La buona terraManifesto del filmTitolo originaleThe Good Earth Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno1937 Durata138 min Dati tecniciB/N in Sepiatonerapporto: 1,37 : 1 Generedrammatico RegiaSidney Franklin SoggettoPearl S. Buck (romanzo) SceneggiaturaTalbot Jennings, Tess Slesinger e Claudine West ProduttoreAlbert Lewin (produttore associato) Produttore esecutivoIrving Thalberg (non accreditato) Casa di produzioneMetro-Goldwyn-Mayer Distribuzione in italiano...

BBC AmericaDiluncurkan29 Maret 1998PemilikBBC WorldwideAMC Theatres(kedua-duanya 50%)NegaraAmerika SerikatBahasaIndonesiaKantor pusatNew York CitySaluran seindukDiscovery NetworksBBC World NewsSitus webbbcamerica.com BBC America adalah stasiun TV BBC yang mengudara di USA. BBC America mempunyai program yang dikirim dari Televisi BBC yang lain. Termasuk program BBC World News America yang ditayangkan simultan dengan BBC World News. BBC America bisa ditonton lewat TV Standard Defintion dan juga...

第三十二届夏季奥林匹克运动会帆船女子風浪板比賽比賽場館神奈川縣藤澤市江之島遊艇港口日期2021年7月25日至31日参赛选手27位選手,來自27個國家和地區奖牌获得者01 ! 卢云秀 中国02 ! 沙利纳·皮康 法国03 ! 埃玛·威尔逊 英国← 20162024 → 2020年夏季奥林匹克运动会帆船比赛项目RS:X级帆板男子女子单人艇雷射型男子单人艇辐射型女子芬蘭�...

まつとも みさき松友 美佐紀Matsutomo Misaki2013年法國羽毛球公開賽基本資料代表國家/地區 日本出生 (1992-02-08) 1992年2月8日(32歲)[1] 日本德島縣板野郡藍住町身高1.59米(5英尺21⁄2英寸)[1]握拍右手[1]主項:女子雙打、混合雙打世界冠軍頭銜 奧運會:1(女雙) 尤伯杯:1職業戰績26勝–16負(女單)419勝–150負(女雙)111勝–119負(混雙)最高世�...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) You can help expand this article with text translated from the corresponding article in Catalan. (December 2017) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the trans...

American college football season 1898 VMI Keydets footballConferenceIndependentRecord4–2Head coachSam Boyle (1st season)Seasons← 18971899 → 1898 Southern college football independents records vte Conf Overall Team W L T W L T North Carolina – 9 – 0 – 0 Central (KY) – 3 – 0 – 1 Oklahoma – 2 – 0 – 0 Navy – 7 – 1 –...



