Nghịch lý Zeno
|
Read other articles:

Feel'eMAlbum mini karya BtoBDirilis6 Maret 2017 (2017-03-06)Direkam2017Genre K-pop Ballad Dance-pop Durasi19:41BahasaKoreaLabel Cube Entertainment LOEN Entertainment Kronologi BtoB New Men(2016) Feel'eM(2017) Singel dalam album Feel'eM SomedayDirilis: 24 Februari 2017 MovieDirilis: 6 Maret 2017 Feel'eM adalah album mini kesepuluh dari grup vokal pria asal Korea Selatan BtoB. Album ini dirilis pada tanggal 6 Maret 2017 oleh Cube Entertainment dibawah pendistribusian oleh LOEN Ente...

Kebudayaan HemuduJangkauangeografisTiongkok TimurPeriodeNeolitikum TiongkokTanggalskt. 5500 – skt. 3300 SMDidahului olehKebudayaan KuahuqiaoDiikuti olehKebudayaan Liangzhu Kebudayaan Hemudu Hanzi: 河姆渡文化 Alih aksara Mandarin - Hanyu Pinyin: Hémǔdù wénhuà Mangkuk tembikar dengan gambar babi, budaya Hemudu Tembikar hitam budaya Hemudu Kebudayaan Hemudu (5500 SM - 3300 SM[1]) merupakan sebuah kebudayaan Neolitik yang berkembang di selatan Teluk Hangzhou di Jiangnan Yuyao ...

Украинские переселенцы в США (Северная Дакота, кон. XIX в.) Драматическое общество им. И. Котляревского (Канада, Виннипег, 1914) Украи́нская эмигра́ция — процесс переселения украинцев за пределы этнических земель (Украины). Массовые переселения украинцев начинаются в...

Artikel ini bukan mengenai Siemens Mobile. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Siemens Mobility – berita · surat kabar · buku · cendekiawan · JSTOR (Februari 2018) Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipe...

Association football club in England Football clubAFC DunstableFull nameAssociation Football ClubDunstableNickname(s)The OD's[1]Founded1981 (as Old Dunstablians)GroundCreasey Park, DunstableCapacity3,065[2]OwnerVarsity NineChairmanDan BediManagerJoe OxleyLeagueSouthern League Division One Central2023–24Southern League Division One Central, 3rd of 19 Home colours Away colours AFC Dunstable are a football club based in Dunstable, Bedfordshire, England. The club are members of ...

Collective head of state of Bosnia and Herzegovina Presidency of Bosnia and HerzegovinaPredsjedništvo Bosne i HercegovineПредсједништво Босне и Херцеговине IncumbentDenis Bećirović Željka Cvijanović Željko Komšićsince 16 November 2022SeatPresidency Building, SarajevoAppointerDirect electionTerm lengthFour yearsrenewable once every individual termFirst holderAlija Izetbegović Momčilo Krajišnik Krešimir ZubakSalary3,091 EUR per month[1]Web...

Comics character The Manhattan GuardianThe Manhattan Guardian by Cameron Stewart.Publication informationPublisherDC ComicsFirst appearanceSeven Soldiers: Guardian #1 (May 2005)Created byGrant MorrisonCameron StewartIn-story informationAlter egoJake JordanTeam affiliationsSeven Soldiers of VictoryNewsboy ArmyJustice LeagueAbilitiesSkilled hand to hand combatantExcellent physical conditionCarries a golden helmet and shield The Manhattan Guardian is a DC Comics costumed hero. Created by Grant Mo...

PDLIM2 التراكيب المتوفرة بنك بيانات البروتينOrtholog search: PDBe RCSB قائمة رموز معرفات بنك بيانات البروتين 2PA1, 3PDV المعرفات الأسماء المستعارة PDLIM2, MYSTIQUE, SLIM, PDZ and LIM domain 2 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 609722 MGI: MGI:2384850 HomoloGene: 11006 GeneCards: 64236 علم الوجود الجيني الوظيفة الجزي�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Great Guitars Joe Louis Walker album – news · newspapers · books · scholar · JSTOR (July 2019) (Learn how and when to remove this message) 1997 studio album by Joe Louis WalkerGreat GuitarsStudio album by Joe Louis WalkerReleasedApril 8, 1997GenreB...

Mappa dei principali aeroporti italiani Gli aeroporti in Italia sono variamente distribuiti nelle varie regioni italiane, e a ciascuno di essi è assegnato un codice aeroportuale ICAO. Il nome, nel caso di aeroporti aperti al traffico civile, è quello della documentazione ufficiale prodotta dall'Ente nazionale per l'aviazione civile (ENAC).[1] Gli aeroporti sono raggruppati distinguendo tra quelli certificati dall'ENAC, presenti nelle liste ENAC e non presenti nelle liste ENAC. Il nu...

A promotional can of Buzz Cola for The Simpsons Movie The long-running television animation The Simpsons has featured a number of fictional products, sometimes spoofs of real-life products, that have subsequently been recreated by real world companies attempting to exploit the popularity of The Simpsons. In 2007, as part of a reverse product placement marketing campaign for The Simpsons Movie, real life versions of a number of Simpsons products were sold in 7-Eleven stores. Real cans of Buzz ...

American politician (born 1974) Kai KaheleMember of the U.S. House of Representativesfrom Hawaii's 2nd districtIn officeJanuary 3, 2021 – January 3, 2023Preceded byTulsi GabbardSucceeded byJill TokudaMember of the Hawaii Senatefrom the 1st districtIn officeFebruary 17, 2016 – December 16, 2020Preceded byGil KaheleSucceeded byLaura Acasio Personal detailsBorn (1974-03-28) March 28, 1974 (age 50)Miloli'i, Hawai'i, U.S.Political partyDemocraticSpouseMaria F...

В Википедии есть статьи о других людях с фамилией Смирнова. Авдотья Смирнова Имя при рождении Авдотья Андреевна Смирнова Дата рождения 29 июня 1969(1969-06-29)[1] (54 года) Место рождения Москва, СССР Гражданство СССР Россия Профессия кинорежиссёр, продюсер, сценари...

Politics of Luxembourg Constitution Law Monarchy Grand Duke (list) Henri Hereditary Grand Duke Prince Guillaume Executive Government: Frieden-Bettel Prime Minister: Luc Frieden Deputy Prime Minister: Xavier Bettel Legislature Chamber of Deputies President: Claude Wiseler Current members Council of State Elections Chamber circonscriptions Recent elections General: 201320182023 European: 201420192024 Communal: 200520112017 Political parties Administrative divisions Cantons Communes Cities Forei...

Low luminosity lenticular galaxy in the constellation Puppis NGC 2328HST image of NGC 2328Observation data (J2000 epoch)ConstellationPuppisRight ascension07h 02m 36.193s[1]Declination−42° 04′ 06.88″[1]Redshift0.003930[2]Heliocentric radial velocity1176.0 km/s[2]Distance59 Mly (18 Mpc)[3]Apparent magnitude (V)12.55[4]Apparent magnitude (B)13.16[4]Absolute magnitude (V)−18.5[3...

La rilevanza enciclopedica di questa voce o sezione sull'argomento calciatori è stata messa in dubbio. Motivo: 32 presenze nella prima divisione panamense, una presenza nella fase finale della CONCACAF League, una presenza in nazionale, però in amichevole, e partecipazione ad un Mondiale Under-20 Puoi aiutare aggiungendo informazioni verificabili e non evasive sulla rilevanza, citando fonti attendibili di terze parti e partecipando alla discussione. Se ritieni la voce non enciclopedic...

Voce principale: Unione Sportiva Alessandria Calcio 1912. Alessandria Unione SportivaStagione 1930-1931Sport calcio Squadra Alessandria Allenatore Béla Révész Presidente Ladislao Rocca Serie A13º posto Maggiori presenzeCampionato: Avalle (32) Miglior marcatoreCampionato: Banchero II (15) StadioCampo del Littorio 1929-1930 1931-1932 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Alessandria Unione Sportiva nelle competizioni ufficiali della...

Questa voce sull'argomento cestisti lettoni è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Edmunds DukulisNazionalità Lettonia Altezza204 cm Peso95 kg Pallacanestro RuoloAla Termine carriera2015 CarrieraGiovanili 2005-2007 BS Riga/Pols2007-2008 ASK Kadeti-2 Riga2013-2014 Boise St. Broncos2014-2015 St. Leo Lions Squadre di club 2008-2010 VEF Rīga31 (441)2009-2010→ BA Turī...
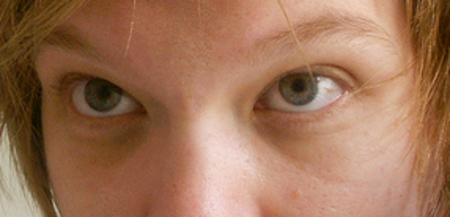
Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Privazione del sonnoOcchiaie e gonfiore periorbitale, tipica condizione che si presenta nei soggetti privati del sonno.Specialitàmedicina del sonno Eziologiainsonnia, sindrome delle apnee nel sonno e disturbo del sonno Classificazione e risorse esterne (EN)MeSHD012892 Modifica dati su Wikidata · Manuale...

293 BCE battle of the Third Samnite War This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2024) (Learn how and when to remove this message) Battle of AquiloniaPart of the Third Samnite WarDate293 BCLocationAquilonia (region around Lazio, Molise, Italy)Result Roman victoryBelligerents Roman Republic SamnitesCommanders and leaders Lucius Papirius Cursor Spur...




