–°–њ–Є—Б–Њ–Ї –њ—А–Њ—Б—В—Л—Е —З–Є—Б–µ–ї
|
Read other articles:

Ernst Benda Ketua Hakim Mahkamah Konstitusi JermanMasa jabatan8 Desember 1971 вАУ 20 Desember 1983 Informasi pribadiKebangsaanJermanProfesiHakimSunting kotak info вАҐ L вАҐ B Ernst Benda (1973) Ernst Benda (1925вАУ2009) adalah Ketua Hakim Mahkamah Konstitusi Jerman. Ia mulai menjabat sebagai ketua hakim di mahkamah tersebut pada tanggal 8 Desember 1971. Di Mahkamah Konstitusi Jerman, ia ditempatkan di Senat Pertama. Masa baktinya sebagai hakim berakhir pada tanggal 20 Desem...

Red Bull Junior TeamBerkas:Red Bull Junior Team Logo 2022.pngBerdiri2001 (2001)Kantor pusat Milton Keynes, InggrisPrinsipal tim Helmut MarkoSitus webhttps://www.redbull.com/int-en/juniorteam Sebastian Vettel dalam Formula 3 Euro Series pada 2006, salah satu pembalap binaan Red Bull. Red Bull Junior Team adalah sebuah program pencarian pembalap muda untuk turun di ajang balap mobil roda terbuka. Ide ini pertama kali terbentuk pada musim 2001, dan telah sukses melahirkan banyak pembalap y...

Druk tsendhenB. Indonesia: Kerajaan Naga Petirаљ†аљЦаЊ≤аљіаљВаЉЛаљЩаљУаЉЛаљСаљУаЉЛLagu kebangsaan BhutanPenulis lirikDorji Lopen Droep Namgay Dasho Gyaldun ThinleyKomponisAku TongmiPenggunaan1953 Druk tsendhen (Kerajaan Naga Petir) adalah lagu kebangsaan negara Bhutan, yang melodinya ditulis oleh Aku Tongmi, dan liriknya ditulis oleh Dasho Gyaldun Thinley. Lagu ini diadopsi sebagai Lagu kebangsaan pada tahun 1953. Lirik Versi asli dalam Bahasa Dzongkha Transliterasi Terjemahan dala...

Bagian dari seriPemelajaran mesindan Penggalian Data Paradigma Pemelajaran terawasi Pemelajaran tak terawasi Pemelajaran mesin daring Pemelajaran mesin luring Meta-learning Pemelajaran semi terawasi Pemelajaran terawasi mandiri Reinforcement learning Pemelajaran berbasis aturan Pemelajaran mesin kuantum Masalah Klasifikasi Model generatif Regresi Kluster Reduksi dimensi Estimasi densitas Deteksi anomali Pembersihan data AutoML Aturan asosiasi Analisis semantik Rekayasa fitur Pemelajaran fitur...

American scientist (1894вАУ1956) Alfred KinseyKinsey in Frankfurt, November 1955BornAlfred Charles Kinsey(1894-06-23)June 23, 1894Hoboken, New Jersey, U.S.DiedAugust 25, 1956(1956-08-25) (aged 62)Bloomington, Indiana, U.S.EducationBowdoin CollegeHarvard University (ScD)Known for Sexology and human sexuality Kinsey Reports Kinsey scale Kinsey Institute for Research in Sex, Gender, and Reproduction Spouse Clara McMillen (m. 1921)Children4Scientific caree...

TulkarmmunaTranskripsi Lainnya вАҐ ArabЎЈўИўДўГЎ±ўЕ вАҐ Ejaan lainTulkarem (resmi)Tul Karem (tak resmi) Lambang TulkarmKegubernuranTulkarmFoundedAbad ke-3Pemerintahan вАҐ JenisKota вАҐ Kepala MunisipalitasMahmoud al-JalladLuas вАҐ Yurisdiksi28,793 dunams (288 km2 or 111 sq mi)Populasi (2007) вАҐ Yurisdiksi61.941 (termasuk kamp pengungsi)Arti namaThe long (place) of the vineyard.[1]...

American Civil War Medal of Honor recipient (1828вАУ1906) Henry T. JohnsBorn(1828-04-08)April 8, 1828Philadelphia, PennsylvaniaDiedMay 13, 1906(1906-05-13) (aged 78)BuriedMountain View Cemetery, Oakland, CaliforniaAllegianceUnited StatesService/branchUnited States ArmyYears of service1862 - 1863, 1864 - 1865RankFirst LieutenantUnitCompany C, 49th Massachusetts Infantry RegimentBattles/warsAmerican Civil WarAwardsMedal of Honor Henry T. Johns (April 8, 1828 - May 13, 1906) was a Unio...

Liga Leumit 1963-1964 Competizione Liga Leumit Sport Calcio Edizione 24¬™ Organizzatore IFA Date dal 12 ottobre 1963all'11 luglio 1964 Luogo Israele Partecipanti 15 Formula 1 girone all'italiana Risultati Vincitore Hapoel Ramat Gan(1¬Ї titolo) Retrocessioni Hapoel Lod Statistiche Miglior marcatore Israel Ashkenazi (21) Incontri disputati 210 Gol segnati 589 (2,8 per incontro) Cronologia della competizione 1962-1963 1964-1965 Manuale La Liga Leumit 1963-1964 √® stata la 24...

Large flightless bird endemic to Australia For other uses, see Emu (disambiguation). EmuTemporal range: Middle Miocene вАУ present PreкЮТ кЮТ O S D C P T J K Pg N MioceneвАУpresent[1] Conservation status Least Concern (IUCN 3.1)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Infraclass: Palaeognathae Order: Casuariiformes Family: Casuariidae Genus: Dromaius Species: D. novaehollandiae Binomial name Dromaius novaeholland...

Henri de Saint-SimonLahirClaude Henri de Rouvroy, comte de Saint-Simon(1760-10-17)17 Oktober 1760Paris, PrancisMeninggal19 Mei 1825(1825-05-19) (umur 64)Paris, PrancisEraFilsafat abad ke-19KawasanFilsafat BaratAliranSaint-SimonianismeSosialismeSosialisme utopisMinat utamaFilsafat politikGagasan pentingPerbedaan kelas industri/kelas pemalas Dipengaruhi Francis Bacon,[1] René Descartes,[1] John Locke,[1] Isaac Newton,[1] David Hume, Edward Gibbon...

Esempio di un tipico ritmo shuffle ascoltaвУШ Swing √® un termine musicale che indica un particolare modo (indicato talvolta come pronuncia swing), tipico della musica jazz, di eseguire le note (in inglese swing notes). Il termine deriva dall'andamento ritmico dondolante che nasce da questa tecnica esecutiva (il verbo inglese to swing significa appunto dondolare). In sintesi, nella pratica, si suonano note terzinate su tempi binari: ad esempio, due crome (note da un ottavo) saranno suonate co...

American football player (1913вАУ2002) American football player Ward CuffNo. 14Position:Halfback, PlacekickerPersonal informationBorn:(1913-08-12)August 12, 1913Redwood Falls, Minnesota, U.S.Died:December 24, 2002(2002-12-24) (aged 89)Vallejo, California, U.S.Height:6 ft 1 in (1.85 m)Weight:192 lb (87 kg)Career informationHigh school:Redwood FallsCollege:MarquetteNFL draft:1937 / Round: 4 / Pick: 34Career history New York Giants (1937вАУ1945) ...

This article is about the software. For other uses, see Blue Jeans (disambiguation). Cloud-based video conferencing service This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on...

Species of flowering plant in the mint and sage family Lamiaceae Salvia hispanica Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Asterids Order: Lamiales Family: Lamiaceae Genus: Salvia Species: S. hispanica Binomial name Salvia hispanicaL. Synonyms[1] Kiosmina hispanica (L.) Raf. Salvia chia Colla Salvia chia Sessé & Moc. nom. illeg. Salvia neohispanica Briq. nom. illeg. Salvia prysmatica Cav. Salvia schiedeana Stap...

This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (December 2022) (Learn how and when to remove this message) Part of a series on theEucharist Lord's Supper Communion Elements Bread Wine Ritual and liturgy Divine Liturgy Holy Qurobo Holy Qurbana Divine Service Mass Requiem Solemn Consecratio...
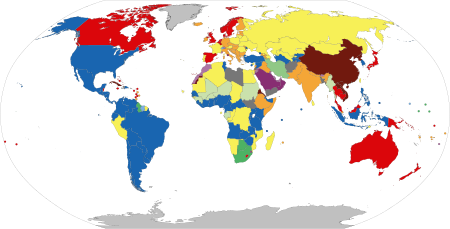
System or group of people governing an organized community, often a state For the executive of parliamentary systems referred to as the government, see Executive (government). For other uses, see Government (disambiguation). Gov redirects here. For other uses, see Gov (disambiguation). World's states coloured by systems of government: Parliamentary systems: Head of government is elected or nominated by and accountable to the legislature Constitutional monarchy with a ceremonial mo...

Ne doit pas √™tre confondu avec Oblast d'Ivano-Frankivsk. Cet article est une √©bauche concernant la Russie. Vous pouvez partager vos connaissances en lвАЩam√©liorant (comment ?) selon les recommandations des projets correspondants. Oblast dвАЩIvanovo (ru) –Ш–≤–∞–љ–Њ–≤—Б–Ї–∞—П –Њ–±–ї–∞—Б—В—М Armoiries de l'oblast d'Ivanovo Drapeau de l'oblast d'Ivanovo Administration Pays Russie R√©gion √©conomique Centre District f√©d√©ral Central Statut politique Oblast Cr√©ation 11 mars 1936 Capitale...

Unter anderem gilt die Tr√§gheit als eines der sieben Hauptlaster. Als Faulheit (abmildernd auch Tr√§gheit genannt) wird der Mangel an erwartbarer Aktivit√§t bei einem Menschen bezeichnet. Der Begriff wird zur Beschreibung und Bewertung von Anstrengungsvermeidern genutzt (genauer: von Menschen, welche aus der Sicht des Sprechers bzw. Schreibers ihrer gesellschaftlich auferlegten Arbeit nicht bzw. nicht mit hinreichendem Flei√Я nachgehen). Die abwertende, oft als beleidigend empfundene Eigensc...

Not to be confused with Your Love (The Outfield song). For the song by Gryffin, see Alive (Gryffin album). 1985 single by BlancmangeLose Your LoveSingle by Blancmangefrom the album Believe You Me B-sideJohnReleased28 October 1985Recorded1985GenreSynth-popLength3:58LabelLondonSire (US)Songwriter(s) Neil Arthur Stephen Luscombe Producer(s)Stewart LevineBlancmange singles chronology What's Your Problem (1985) Lose Your Love (1985) I Can See It (1986) Alternative coverCanadian cover of Lose Your ...

American writer (1927вАУ2003) For his grandfather, the publisher and philanthropist, see George Arthur Plimpton. George PlimptonPlimpton in 1977BornGeorge Ames Plimpton(1927-03-18)March 18, 1927New York City, U.S.DiedSeptember 25, 2003(2003-09-25) (aged 76)New York City, U.S.EducationHarvard University (BA)King's College, Cambridge (BA)Occupations Writer journalist literary editor actor Spouses Freddy Medora Espy (m. 1968; div. 1988) Sa...




























