–Я—А–Њ—Б—В–Њ–µ —З–Є—Б–ї–Њ –Т–Њ–ї—М—Б—В–µ–љ—Е–Њ–ї—М–Љ–∞
|
Read other articles:

Anhar Gonggong, Tenaga Profesional Bidang Sosial Budaya dan Kepemimpinan Lembaga Ketahanan Nasional RI Dr. Anhar Gonggong, M.A. (lahir 14 Agustus 1943) adalah sejarawan dan birokrat Indonesia.[1] Keluarga Atas nama penumpasan pemberontakan, pasukan Depot Speciale Troepen yang dipimpin Kapten Raymond Pierre Paul Westerling menyisir desa-desa di Sulawesi Selatan. Hanya sekitar tiga bulan dari Desember 1946 hingga Februari 1947, ribuan nyawa melayang dan darah tertumpah di sana.[2 ...

Penggambaran Bigtan dan Teresh karya Antoine Caron. Bigtan dan Teresh atau Bigtan dan Teresy adalah dua kasim yang melayani raja Persia Ahasuerus, menurut Kitab Ester. Mordecai berrehat di halaman istana selama sehari dan mendengar dua kasim tersebut yang berrencana untuk membunuh sang raja. Ia memberitahukan sang raja melalui Ester, sehingga rencana tersebut menjadi terbongkar. Ia dihargai oleh sang raja pada masa setelahnya.[1] Dalam kitab deuterokanonika/apokrifa berjudul Tambahan-...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Liebes...

ўЖўКЎІ Ў£Ў±Ў™ЎІўГўК ќЭќ≠ќ± ќСѕБѕДќђќЇќЈ Nea Artaki ЎЃЎ±ўКЎЈЎ© ЎІўДўЕўИўВЎє Ў™ўВЎ≥ўКўЕ Ў•ЎѓЎІЎ±ўК ЎІўДЎ®ўДЎѓ ЎІўДўКўИўЖЎІўЖ[1] ЎІўДўЕўЖЎЈўВЎ© ЎІўДЎ•ЎѓЎІЎ±ўКЎ© ўИЎ≥ЎЈ ЎІўДўКўИўЖЎІўЖ Ў•ўКўБўКЎІ ЎЃЎµЎІЎ¶Ўµ ЎђЎЇЎ±ЎІўБўКЎ© Ў•Ў≠ЎѓЎІЎЂўКЎІЎ™ 38¬∞31вА≤00вА≥N 23¬∞38вА≤00вА≥E / 38.51666667¬∞N 23.63333333¬∞E / 38.51666667; 23.63333333 ЎІўДўЕЎ≥ЎІЎ≠Ў© 2194 ўГўКўДўИўЕЎ™Ў± ўЕЎ±Ў®Ўє ЎІўДЎ£Ў±Ўґ 23.015 ўГўЕ¬≤ ЎІўДЎІЎ±Ў™ўБЎІЎє 11 ўЕЎ™Ў± ЎІўДЎ≥ўГЎІпњљ...

Giovanni Ferrari FBC Juventus - 1930-anInformasi pribadiTanggal lahir (1907-12-06)6 Desember 1907Tempat lahir Alessandria, ItaliaTanggal meninggal 2 Desember 1982(1982-12-02) (umur 74)Tempat meninggal Milan, ItaliaPosisi bermain Pemain tengahKarier senior*Tahun Tim Tampil (Gol)1923вАУ1925 Alessandria 17 (2)1925вАУ1926 FBC Internaples 15 (16)1926вАУ1930 Alessandria 105 (60)1930вАУ1935 Juventus 160 (66)1935вАУ1940 Ambrosiana/Inter 108 (24)1940вАУ1941 Bologna 16 (2)1941вАУ1942 Juventus 6 (...

Museum of European history in Brussels, Belgium This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (March 2024) (Learn how and when to remove this template message) House of European History (HEH)House of European History in the former Eastman Building, Leopold Park, BrusselsFormer namesEastman Dental HospitalEastma...

1938 film This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Citadel 1938 film вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (January 2017) (Learn how and when to remove this template message) The CitadelDirected byKing VidorScreenplay byIan DalrympleFrank WeadElizabeth HillBased onThe Citadel1937 nove...

Finnish savoury pie This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kalakukko вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (August 2009) (Learn how and when to remove this template message) KalakukkoTypeSavoury piePlace of originFinlandRegion or stateNorthern SavoniaMain ingredientsBread (rye flour), fish (...

Process of attracting, selecting and appointing candidates to a job or other organization This article is about filling vacancies in an organization. For other uses, see Recruitment (disambiguation) and Recruit (disambiguation). Recruitment poster for the UK army Recruitment is the overall process of identifying, sourcing, screening, shortlisting, and interviewing candidates for jobs (either permanent or temporary) within an organization. Recruitment also is the process involved in choosing p...

Formula One 2003 PublikasiGenreRacingKarakteristik teknisPlatformPlayStation 2 Modepermainan video multipemain FormatDVD Format kode Daftar 30 Informasi pengembangPengembangSony Studio LiverpoolPenyuntingSony Interactive Entertainment PenerbitSCEEInformasi tambahanSitus webpt.playstation.comвА¶ MobyGamesformula-one-2003 Portal permainan videoSunting di Wikidata вАҐ L вАҐ B вАҐ PWBantuan penggunaan templat ini Formula One 2003 merupakan permainan video yang berbasis dari seri ba...

Great Falls, MontanaCityGreat Falls, Montana as viewed from Interstate 15, looking due north LambangJulukan: The Electric CityLocation of Great Falls, MontanaCountryUnited StatesStateMontanaCountyCascadePemerintahan вАҐ MayorMichael WintersLuas[1] вАҐ City22,26 sq mi (57,65 km2) вАҐ Luas daratan21,79 sq mi (56,44 km2) вАҐ Luas perairan0,47 sq mi (1,22 km2)Ketinggian3.330 ft (1.015 m)Pop...

Questa voce sull'argomento stagioni delle societ√† calcistiche italiane √® solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Unione Sportiva Fiumana. Unione Sportiva FiumanaStagione 1941-1942Sport calcio Squadra Fiumana Allenatore Angelo Piccaluga Presidente Carlo Descovich Serie B15¬Ї posto. Retrocessa in Serie C. Coppa ItaliaSedicesimi di finale. Maggiori presenzeCampionato: Poggi (2...

ўЗўЖўИЎѓўЕЎєўДўИўЕЎІЎ™ ЎєЎІўЕЎ©ўЖЎ≥Ў®Ў© ЎІўДЎ™Ў≥ўЕўКЎ© ЎІўДўЗўЖЎѓ ЎІўДЎ™ЎєЎѓЎІЎѓ ЎІўДўГўДўКЎІўДЎ™ЎєЎѓЎІЎѓ ўВЎ±ЎІЎ®Ў©вАЙ1.21 ўЕўДўКЎІЎ±[1][2]Ў™ЎєЎѓЎІЎѓ ЎІўДўЗўЖЎѓ ЎєЎІўЕ 2011ўВ.вАЙ1.32 ўЕўДўКЎІЎ±[3]Ў™ўВЎѓўКЎ±ЎІЎ™ ЎєЎІўЕ 2017ўВ.вАЙ30.8 ўЕўДўКўИўЖ[4]ўЕўЖЎІЎЈўВ ЎІўДўИЎђўИЎѓ ЎІўДўЕўЕўКЎ≤Ў©Ў®ўДЎѓ ЎІўДЎ£ЎµўД ЎІўДўЗўЖЎѓ ЎІўДЎ®ўДЎѓ ЎІўДўЗўЖЎѓ ЎІўДўЗўЖЎѓ ўЖўКЎ®ЎІўД 4,000,000[5] ЎІўДўИўДЎІўКЎІЎ™ ЎІўДўЕЎ™Ў≠ЎѓЎ© 3,982,398[6] ЎІўДЎ•ўЕЎІЎ±...

Luigi ZarconePersonal informationNationalityItalianBorn(1950-06-18)18 June 1950Villabate, ItalyDied9 June 2001(2001-06-09) (aged 50)Palermo, ItalySportCountry ItalySportAthleticsEvent(s)Middle distance runningLong distance runningClubG.S. Fiamme GialleAchievements and titlesPersonal bests 800 m: 1:49.6 (1976) 1500 m: 3:37.7 (1974) 3000 m: 7:47.54 (1977) 5000 m: 13:23.7 (1977) 10000 m: 28:02.3 (1977) Medal record Mediterranean Games 1979 Split 5000 metres 1979 Split 10000 metres Luigi Zar...

Neutron Star Collision (Love Is Forever)Singel oleh Musedari album The Twilight Saga: Eclipse (soundtrack)Dirilis17 Mei 2010FormatDigital downloadGenreRock alternatifDurasi3:50LabelWarner Bros. RecordsPenciptaMatthew BellamyProduserButch Vig Neutron Star Collision (Love Is Forever) (Tabrakan Bintang Neutron (Cinta Ini Selamanya)) adalah lagu dari band asal Inggris beraliran rock alternatif, Muse. Lagu yang termasuk ke dalam original soundtrack film The Twilight Saga: Eclipse. Direkam tahun 20...

Israeli police officers. According to the Israel Police, the general crime rate dropped in 2020, while cyber crimes, domestic violence and sexual abuse incidents rose.[1] Homicide In Israel the homicide rate is relatively low: in 2015, there were 2.4 people killed per 100,000 inhabitants (in Switzerland the number is 0.71, in Russia it is 14.9, in South Africa it is 34, in Venezuela it is 49).[2] In 2009, 135 people were murdered in Israel. Six Israeli women were killed by pa...

Davide Astori Astori di bulan Juni 2015.Informasi pribadiTanggal lahir (1987-01-07)7 Januari 1987Tempat lahir San Giovanni Bianco, ItaliaTanggal meninggal 4 Maret 2018(2018-03-04) (umur 31)Tempat meninggal Udine, ItaliaTinggi 188 m (616 ft 10 in)[1]Posisi bermain Bek tengahInformasi klubKlub saat ini FiorentinaNomor 13Karier junior Pontisola2001вАУ2006 MilanKarier senior*Tahun Tim Tampil (Gol)2006вАУ2008 Milan 0 (0)2006вАУ2007 вЖТ Pizzighettone (pinjaman) 25 (1)20...

Sports arena in Melbourne, Victoria 37¬∞52вА≤50.322вА≥S 145¬∞12вА≤42.029вА≥E / 37.88064500¬∞S 145.21167472¬∞E / -37.88064500; 145.21167472 State Basketball CentreThe SBC's show court, February 2021LocationWantirna South, Victoria, AustraliaCapacity3,200ConstructionBroke ground2011Opened22 June 2012[1]Construction costA$27m[2]TenantsKnox Raiders (NBL1 South) (2012вАУpresent)Melbourne Boomers (WNBL) (2013вАУ2023)Southside Flyers (WNBL) (2022вАУpresent)Sou...

FC SchaffhausenCalcio FCS, Gelb-Schwarz (giallo-neri), B√ґcke (arieti) Segni distintiviUniformi di gara Casa Trasferta Colori sociali Giallo, nero Dati societariCitt√†Sciaffusa Nazione Svizzera ConfederazioneUEFA Federazione ASF/SFV CampionatoChallenge League Fondazione1896 Presidente Roland Klein Allenatore Bigi Meier StadioBerformance Arena(8.100 posti) Sito webwww.fcschaffhausen.ch Palmar√®sTitoli nazionali2 campionati di Challenge League/Lega Nazionale B4 campionati di terza serie Si...
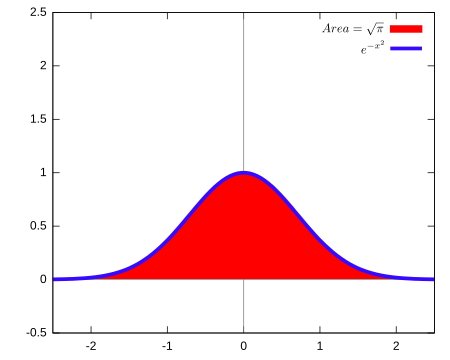
Grafik dari fungsi f(x) = eвИТx2 dan luas di antara fungsi tersebut dan sumbu x (yakni, di sepanjang garis), sama dengan π {\displaystyle \scriptstyle {\sqrt {\pi }}} . Integral Gauss, juga dikenal dengan nama integral EulerвАУPoisson, merupakan integral dari fungsi Gauss eвИТx2 di sepanjang garis real. Integral ini dinamai dari matematikawan Jerman Carl Friedrich Gauss, yang dirumuskan sebagai ∫ − ∞ ∞ e − x 2 d x = π {\displaystyle \int _...




