사용대차

사용대차(使用貸借)는 당사자의 일방(貸主)이 상대방(借主)에게 무상으로 사용·수익하게 하기 위하여 목적물을 인도할 것을 약정하고 상대방은 이를 사용·수익한 후 그 물건을 반환할 것을 약정함으로써 성립하는 계약이다(609조). 사용대차 계약은 무상계약, 편무계약, 낙성계약, 계속적 계약에 속한다. 대한민국의 구 민법에서는 낙성계약이 아닌, 요물계약이었다.[1] 사용대차는 빌린 물건 그 자체를 반환한다는 점에서 소비대차와 다르고 임대차와 같으며, 사용·수익의 대가를 지급하지 않는 점에서 임대차와 다르다. 사용대차는 무상으로 동산·부동산으로부터 금전이나 유가증권까지 목적으로 할 수 있으므로 친근하고 특수한 관계에 있는 자 사이에서만 많이 성립하게 되어 이 점에서 법률관계로서의 문제는 적다. 사용대차는 낙성계약이므로 대주는 목적물을 차주에게 인도할 의무가 있다. 또한 그 뒤에도 대주는 차주에게 목적물의 사용·수익을 허용하여야 할 의무가 있다. 그러나 임대인과 같이 목적물을 수선하여 이용에 적합하도록 해줄 적극적인 의무는 없다. 또 무상이기 때문에 대주의 담보책임은 증여자와 같이 가볍다(612조). 차주는 물건을 사용·수익하고 사용대차의 종료 후에는 원상으로 회복하여 목적물을 반환하여야 한다(615조).[2]

각주

  1. ↑ 《글로벌 세계대백과》〈낙성계약·요물계약〉
  2. ↑ 《글로벌 세계대백과》〈사용대차〉
이 문서에는 다음커뮤니케이션(현 카카오)에서 GFDL 또는 CC-SA 라이선스로 배포한 글로벌 세계대백과사전의 내용을 기초로 작성된 글이 포함되어 있습니다.

Read other articles:

Холокост на Украине

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

 

منتخب كوراساو لكرة القدم

منتخب كوراساو لكرة القدم معلومات عامة بلد الرياضة  كوراساو الفئة كرة القدم للرجال  رمز الفيفا CUW  الاتحاد اتحاد كوراساو لكرة القدم كونفدرالية كونكاكاف (أمريكا الشمالية والوسطى والكاريبي) الملعب الرئيسي ملعب إرغيليو هاتو الموقع الرسمي الموقع الرسمي  الطاقم والل...

 

Mahasiswa

Dua mahasiswa sedang berdiskusi. Mahasiswa adalah sebutan bagi orang yang sedang menempuh pendidikan tinggi di sebuah perguruan tinggi yang terdiri dari Universitas, Institut, Sekolah Tinggi, Politeknik, Akademi, dan Akademi Komunitas. Hingga saat ini, mahasiswa di berbagai negara mengambil peran penting dalam sejarah suatu negara. yang terjadi di Indonesia, misalnya yang saling bersangkutan, Tragedi Orde Lama yang dilanjutkan Tragedi Orde Baru: Pada 1965, ribuan mahasiswa berhasil mendesak P...

Samuel C. Fessenden

American attorney and politician (1815–1882) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (August 2022) (Learn how and when to remove this template message) Samuel C. FessendenMember of the U.S. House of Representativesfrom Maine's 3rd districtIn officeMarch 4, 1861 – March 3, 1863Preceded byEzra B. FrenchSucceeded byJames G. Blaine...

 

Achmad Albar

Ahmad Syech Albar beralih ke halaman ini. Untuk komedian Indonesia dengan nama lahir yang sama, lihat Bing Slamet. Achmad AlbarLahirAchmad Syech Albar16 Juli 1946 (umur 77)Surabaya, Jawa Timur, IndonesiaPekerjaan Penyanyi-penulis lagu aktor musisi Suami/istriRini S. Bono ​ ​(m. 1978; c. 1994)​ Dewi Sri Astuti ​(m. 2009)​Anak4Orang tuaSyech Albar (bapak)Farida Al-Hasni (ibu)Karier musikGenre Hard rock power pop d...

 

Carolina Panthers

Carolina Panthers Musim saat iniDidirikan 1993Bermain di Bank of America StadiumKantor pusat di Charlotte, North Carolina Carolina Panthers helmetCarolina Panthers logoHelmLogoAfiliasi liga National Football League (1995–sekarang) National Football Conference (1995–present) NFC West (1995–2001) NFC South (2002–present) Seragam saat iniWarna timBlack, Panther Blue, Silver, White        MaskotSir PurrPersonelPemilikDavid TepperPresidenTom GlickPelatih utamaRon Ri...

Calibration curve

Method for determining the concentration of a substance in an unknown sample This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2008) (Learn how and when to remove this template message) This article's ...

 

Человек прямоходящий

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

 

Creation science

Pseudoscientific form of Young Earth creationism Not to be confused with Christian Science. Part of a series onCreationism History Types Young Earth Time dilation creationism Old Earth day-age gap progressive Neo-creationism Biblical cosmology Book of Genesis creation narrative framework interpretation as an allegory Omphalos hypothesis Creation science Created kind Flood geology Creationist cosmologies Intelligent design Rejection of evolution by religious groups History Public education Te...

Friedrich Kalkbrenner

German pianist The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (October 2020) (Learn how and when to remove this message) Kalkbrenner by Henri Grévedon, 1829 Friedrich Wilhelm Michael Kalkbrenner (7 November 1784 – 10 June 1849), also known as Frédéric Kalkbrenner, was a pianist, composer, piano teacher and piano manufacturer. German by birth, Kalkbrenner studied at the Con...

 

One Rockwell West Tower

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: One Rockwell West Tower – news · newspapers · books · scholar · JSTOR (July 2018) (Learn how and when to remove this message) Residence in Makati, PhilippinesOne Rockwell TowersGeneral informationStatusCompletedTypeResidenceLocationMakati, PhilippinesCoordinate...

 

The Last Innocents

2016 book by Michael Leahy The Last Innocents:The Collision of the Turbulent Sixties and the Los Angeles Dodgers AuthorMichael LeahyCountryUnited StatesLanguageEnglishGenreNon-fictionPublisherHarperCollinsPublication dateMay 10, 2016ISBN978-0-06-236056-4 The Last Innocents: The Collision of the Turbulent Sixties and the Los Angeles Dodgers is a book by author Michael Leahy, centered around the Los Angeles Dodgers teams of the 1960s. The book was the winner of the 2016 Casey Award as the best ...

Sparatoria di Tucson del 2011

Sparatoria di Tucson del 2011attentatoL'esterno del supermercato Safeway, luogo della sparatoria Tipo Sparatoria Tentato omicidio Data8 gennaio 201110:10 (UTC-7) LuogoCasas Adobes Stato Stati Uniti Stato federato Arizona ComuneTucson Coordinate32°20′09.5″N 110°58′30.5″W / 32.335972°N 110.975139°W32.335972; -110.975139Coordinate: 32°20′09.5″N 110°58′30.5″W / 32.335972°N 110.975139°W32.335972; -110.975139 ObiettivoGabrielle Giffo...

 

克莱门特·艾德礼

艾德礼伯爵 阁下The Rt Hon. The Earl AttleeKG OM CH PC FRS联合王国首相任期1945年7月26日—1951年10月26日君主乔治六世副职赫伯特·莫里森前任温斯顿·丘吉尔继任温斯顿·丘吉尔联合王国副首相任期1942年2月19日—1945年5月23日（战时内阁）君主乔治六世首相温斯顿·丘吉尔前任职位创立继任赫伯特·莫里森反对党领袖任期1951年10月26日—1955年11月25日君主乔治六世伊丽莎白二�...

 

2016年美國總統選舉

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 %   获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

محمد بن سعود بن عبد العزيز آل سعود

محمد بن سعود بن عبد العزيز آل سعود أمير منطقة الباحة في المنصب1407هـ – 1431هـ العاهل فهد بن عبد العزيز وعبد الله بن عبد العزيز . النائب فيصل محمد بن سعود إبراهيم بن محمد الزيد مشاري بن سعود بن عبد العزيز آل سعود وزير المالية في المنصب1381 هـ – 1381 هـ (ستة أيام) العاهل سعود بن عبد الع...

 

Drinking straw

Thin tube for drinking liquids Plastic drinking straws with bellows segment A drinking straw is a utensil that is intended to carry the contents of a beverage to one's mouth. Disposable straws are commonly made from plastics. However, environmental concerns related to plastic pollution and new regulation have led to rise in reusable and biodegradable straws. Following a rise in regulation and public concern, some companies have even voluntarily banned or reduced the number of plastic straws u...

 

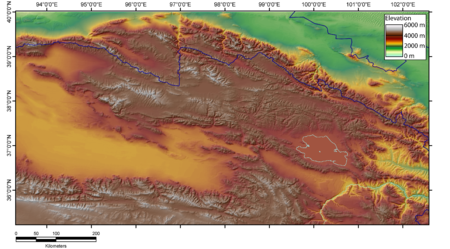
Qilian Mountains

Mountain range in China 39°12′N 98°32′E / 39.200°N 98.533°E / 39.200; 98.533 Qilian Mountains祁連山Qilian Mountains in Qilian County, QinghaiHighest pointPeakKangze'gyaiElevation5,808 m (19,055 ft)Geography LocationGansu and Qinghai provinces, China The Qilian Mountains (simplified Chinese: 祁连山; traditional Chinese: 祁連山; pinyin: Qílián Shān; Wade–Giles: Ch'i2-lien2 Shan1, also romanized as Tsilien; Mongghul: Ch...

Peter Snow

British television presenter (born 1938) For other people named Peter Snow, see Peter Snow (disambiguation). Peter SnowCBEBornPeter John Snow (1938-04-20) 20 April 1938 (age 86)Dublin, Ireland[1]Alma materBalliol College, OxfordOccupationsTelevision journalistradio broadcasterhistorianYears active1962-presentKnown forSwingometerTelevisionITN Defence and Diplomatic Correspondent (1966–1979)ITN General Election programmes (1966–1979)Newsnight (1980–1997)BBC Gen...

 

Adjunction space

In mathematics, an adjunction space (or attaching space) is a common construction in topology where one topological space is attached or glued onto another. Specifically, let X and Y be topological spaces, and let A be a subspace of Y. Let f : A → X be a continuous map (called the attaching map). One forms the adjunction space X ∪f Y (sometimes also written as X +f Y) by taking the disjoint union of X and Y and identifying a with f(a) for all a in A. Formally, X ∪ f Y = ( X &#...