確率微分方程式
|
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Sistem otomatisasi kantor – berita · surat kabar · buku · cendekiawan · JSTORArtikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan ...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (août 2023). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » En pratique : Quelles sources sont attendues ? Comm...

US online nonprofit news outlet For other uses, see Intercept (disambiguation). The InterceptScreenshot Type of siteNews websiteAvailable inEnglishPortugueseURLtheintercept.com CommercialNoLaunchedFebruary 2014 Photograph by Trevor Paglen of the National Security Agency headquarters in Fort Meade first published in The Intercept The Intercept is an online American nonprofit news organization that publishes articles and podcasts. The Intercept has published in English since its founding i...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Pura Mangkunagaran – berita · surat kabar · buku · cendekiawan · JSTORPura Mangkunagaranꦦꦸꦫꦩꦁꦏꦸꦤꦒꦫꦤ꧀Purå MangkunagaranBagian depan Pendopo Ageng Pura Mangkunegaran.Informasi umu...

For the name, see Glomb (surname). Glide bomb Glomb Pratt-Read LBE-1 GlombTypeGlide bombPlace of originUnited StatesService historyIn service1944–1945Used byUnited States NavyWarsWorld War II (test only) Glomb, from glide bomb, was a project undertaken by the United States Navy during World War II to develop an unmanned aircraft for delivering bombs to high-value, well-protected targets without risk to aircrew. The project proceeded through the war, producing several pro...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: St. John Vianney High School Kirkwood, Missouri – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this template message) Private, all-boys school in Kirkwood, , Missouri, United StatesSt. John Vianney High SchoolAddres...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 2002 West Virginia Senate election – news · newspapers · books · scholar · JSTOR (February 2024) 2002 West Virginia Senate elections ← 2000 November 5, 2002 2004 → ← These seats' last election (1998)These seats' next e...

Indian politician, Advocate and social worker B. John PandianB. John Pandian in 2020State Youth Wing Secretary, Pattali Makkal KatchiIn office1989–1996Founder & Chairman of Devendrar College of PhysiotherapyIncumbentAssumed office 1998Founder and leader of Tamizhaga Makkal Munnetra KazhagamIncumbentAssumed office 2000 Personal detailsBornB. John Pandian (1955-11-30) 30 November 1955 (age 68)Sivalarkulam,AlangulamTirunelveli District,Madras State(now in Tenkasi district,Tami...

Chemical compound SaripidemClinical dataATC codenoneIdentifiers IUPAC name N-[[2-(4-chlorophenyl)imidazo[1,2-a]pyridin-3-yl]methyl]-N-methylbutanamide CAS Number103844-86-6 NPubChem CID3058746ChemSpider2319846 YUNII0J6174G60NChEMBLChEMBL73416 YCompTox Dashboard (EPA)DTXSID60146110 Chemical and physical dataFormulaC19H20ClN3OMolar mass341.84 g·mol−13D model (JSmol)Interactive image SMILES O=C(N(C)Cc1c(nc2ccccn12)c3ccc(Cl)cc3)CCC InChI InChI=1S/C19H20ClN3O/c1-3-6-18(24)22...

Disambiguazione – Se stai cercando la vecchia stazione chiusa nel 1931, vedi Stazione di Milano Lambrate (1906). Milano Lambratestazione ferroviaria LocalizzazioneStato Italia LocalitàMilano, quartiere Lambrate Coordinate45°29′05.76″N 9°14′14.4″E / 45.484933°N 9.237333°E45.484933; 9.237333Coordinate: 45°29′05.76″N 9°14′14.4″E / 45.484933°N 9.237333°E45.484933; 9.237333 Altitudine125 m s.l.m. LineeMilano-VeneziaMilano-Bologn...

Opera by Ambroise Thomas For other uses, see Mignon (disambiguation). MignonOpera by Ambroise ThomasPoster for the premiere, by Jules ChéretLibrettist Jules Barbier Michel Carré LanguageFrenchBased onWilhelm Meisters Lehrjahreby GoethePremiere17 November 1866 (1866-11-17)Opéra-Comique, Paris Mignon is an 1866 opéra comique (or opera in its second version) in three acts by Ambroise Thomas. The original French libretto was by Jules Barbier and Michel Carré, based on Goethe's...

Questa voce o sezione sull'argomento sceneggiatori non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Charles Spaak Charles Spaak (Saint-Gilles, 25 maggio 1903 – Nizza, 4 marzo 1975) è stato uno sceneggiatore belga. Biografia Sia il padre che la madre erano politici belgi. Il padre, Paul, era avvocato e d...

Anarchism Project‑class Anarchism portalThis page is within the scope of WikiProject Anarchism, a collaborative effort to improve the coverage of anarchism on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.AnarchismWikipedia:WikiProject AnarchismTemplate:WikiProject Anarchismanarchism articlesProjectThis page does not require a rating on Wikipedia's content assessment scale. Anarchism WikiProject o...

American actress This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2013) (Learn how and when to remove this message) Marian MercerBornMarian Ethel Mercer(1935-11-26)November 26, 1935Akron, Ohio, U.S.DiedApril 27, 2011(2011-04-27) (aged 75)Newbury Park, California, U.S.Alma materUniversity of MichiganYears active1955-2000Spouse(s)Martin Ca...
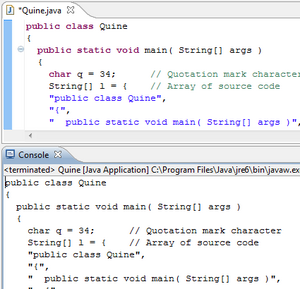
Self-replicating program A quine's output is exactly the same as its source code (the syntax highlighting demonstrated by the text editor in the upper half of the image does not affect the output of the quine). A quine is a computer program that takes no input and produces a copy of its own source code as its only output. The standard terms for these programs in the computability theory and computer science literature are self-replicating programs, self-reproducing programs, and self-copying ...

Campaign against Late Postclassic Maya See also: Spanish conquest of Guatemala and Spanish conquest of Petén vteSpanish conquestof the Maya Chiapas Guatemala Petén Yucatán vteSpanish colonial campaigns 15th century Canary Islands (1402–96) Santa Cruz de la Mar Pequeña (1478) Guinea (1478) Algeria (1497) Melilla (1497) 16th century Algeria (1505) Algeria (1507) Morocco (1508) Algeria (1509) Algeria (1510) Tripoli (1510) Tunisia (1510) Puerto Rico (1511–29) Algeria (1516) Algeria (1517�...

Cinema of theUnited Kingdom List of British films British horror 1888–1919 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 19841985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 19941995...

Tesaurus Tesaurus merupakan sebuah buku sinonim (dua kata atau lebih yang memiliki arti yang sama). Tesaurus sering termasuk karya terkait yang memiliki hal yang hampir sama. Beberapa tesaurus juga termasuk daftar hiponim (sub-bagian, misalnya mawar adalah hiponim dari bunga) yang sering digunakan, serta antonim (dua kata yang memiliki arti berlawanan). Sebagai contoh, dengan mencari kata besar di sebuah tesaurus, seseorang akan menemukan kata lain yang mirip seperti raya, agung, dll. Jika se...

CharlotteCharlotte, Haryapatih Luksemburg, 1942.Haryapatih LuksemburgBerkuasa14 Januari 1919 – 12 November 1964PendahuluMarie-AdélaïdePenerusJeanInformasi pribadiKelahiran(1896-01-23)23 Januari 1896Puri Berg, LuksemburgKematian9 Juli 1985(1985-07-09) (umur 89)Puri Fischbach, LuksemburgPemakamanKatedral Notre-Dame, LuksemburgWangsaWangsa Nassau-Weilburg(melalui kelahiran)Wangsa Bourbon-Parma(melalui perkawinan)Nama lengkapCharlotte Adelgonde Elisabeth Marie WilhelmineAyahGuillaume IV ...

Specialist police force in Merseyside, England Law enforcement agency Mersey Tunnels PoliceLogo of the Mersey Tunnels PoliceAbbreviationMTPAgency overviewFormed1936Jurisdictional structureLegal jurisdictionMersey Tunnels and approachesGoverning bodyMerseytravelConstituting instrumentSection 105 of the County of Merseyside Act (1980)General natureCivilian policeOperational structureHeadquartersGeorges Dock Building, Georges Dockway, LiverpoolOfficers51 (2015)FacilitiesStations1WebsiteOfficial ...




![{\displaystyle \mu :\mathbb {R} ^{n}\times [0,T]\to \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/265933d23389f722cca12696c531283cc5687fda)
![{\displaystyle \sigma :\mathbb {R} ^{n}\times [0,T]\to \mathbb {R} ^{n\times m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a94bbea7c7aaeeb74145170b9e082e9f67db8b13)



![{\displaystyle \mathbb {E} {\big [}|Z|^{2}{\big ]}<+\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/debb044a448f823733b4b5004061f5be9659f60a)



![{\displaystyle \mathbb {E} \left[\int _{0}^{T}|X_{t}|^{2}\,\mathrm {d} t\right]<+\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cc3220b37835b46425072e582c974c424516538)