微分作用素
|
Read other articles:

The Right HonourableEd MilibandMPEd Miliband, 2020 Pemimpin Oposisi Britania RayaMasa jabatan25 September 2010 – 8 May 2015Penguasa monarkiElizabeth IIPerdana MenteriDavid CameronWakilHarriet Harman PendahuluHarriet HarmanPenggantiHarriet HarmanPemimpin Partai BuruhMasa jabatan25 September 2010 – 8 May 2015WakilHarriet Harman PendahuluGordon BrownPenggantiJeremy CorbynMenteri Energi dan Perubahan IklimMasa jabatan3 Oktober 2008 – 11 Mei 2010Perdana MenteriGord...

Agostino CasaroliSekretaris NegaraTakhtaPorto-Santa RufinaPenunjukan1 Juli 1979Masa jabatan berakhir1 Desember 1990PendahuluJean-Marie VillotPenerusAngelo SodanoJabatan lainKardinal-Uskup Porto-Santa RufinaKardinal-Imam Santi XII ApostoliImamatTahbisan imam27 Mei 1937Tahbisan uskup16 Juli 1967oleh Paus Paulus VIPelantikan kardinal30 Juni 1979oleh Yohanes Paulus IIPeringkatKardinal-ImamInformasi pribadiLahir(1914-11-24)24 November 1914Castel San Giovanni, ItaliaWafat9 Juni 1998(1998-06-09...

Al Mahrah المهرةKegubernuranNegaraYamanIbu kotaAl GhaydahLuas • Total82.405 km2 (31,817 sq mi)Populasi[1] • Total108.000 • Kepadatan0,0.013/km2 (0,0.034/sq mi) Al Mahrah atau Mahra (Arab: المهرةcode: ar is deprecated Al Mahra) adalah sebuah kegubernuran di Yaman, yang beribu kota di Al Ghaydah. Distrik Distrik Al Ghaydah Distrik Al Masilaht Distrik Hat Distrik Hawf Distrik Huswain Distrik Man'ar Distrik Qishn Distrik ...
Val CamonicaMonte Concarena, media Val CamonicaStati Italia Regioni Lombardia Province Brescia Bergamo Località principaliAngolo Terme, Artogne, Berzo Demo, Berzo Inferiore, Bienno, Borno, Braone, Breno, Capo di Ponte, Castro, Cedegolo, Cerveno, Ceto, Cevo, Cimbergo, Cividate Camuno, Corteno Golgi, Darfo Boario Terme, Edolo, Esine, Gianico, Incudine, Losine, Lovere, Lozio, Malegno, Malonno, Monno, Niardo, Ono San Pietro, Ossimo, Paisco Loveno, Paspardo, Pian Camuno, Pianc...

Pour les articles homonymes, voir ADF. Assemblée des départements de France Cadre But Défense de l'intérêt des départements Zone d’influence France Fondation Fondation 11 septembre 1946 Fondateur Aimé Malécot, Loire, président fondateur Identité Siège Paris (Île-de-France) Président François Sauvadet[1] Vice-présidents Martine Vassal, Première Vice-Présidente - Bouches du Rhône Frédéric Bierry, Vice-Président, Président de la commission Solidarité, santé et travail ...
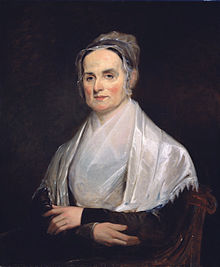
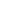
Liste des signataires de la Déclaration de sentiments de 1848. La Convention de Seneca Falls, tenue les 19 et 20 juillet 1848 à Seneca Falls (New York), fut la première convention pour les droits des femmes à se dérouler sur le sol des États-Unis[1]. Elle réunit environ deux cents personnes parmi lesquelles Elizabeth Cady Stanton, Lucretia C. Mott et Abby Kelley trois figures marquantes du mouvement féministe américain, et plusieurs représentants du mouvement abolitionniste tel l'or...

Liège-Bastogne-Liège 2018 GénéralitésCourse104e Liège-Bastogne-LiègeCompétitionUCI World Tour 2018 1.UWTDate22 avril 2018Distance258,5 kmPays BelgiqueLieu de départLiègeLieu d'arrivéeAnsÉquipes25Partants175Arrivants132Vitesse moyenne40,314 km/hSite officielSite officielRésultatsVainqueur Bob Jungels (Quick-Step Floors)Deuxième Michael Woods (EF Education First-Drapac)Troisième Romain Bardet (AG2R La Mondiale) ◀20172019▶Documentation Le Liège-Bastogne-Liège 2018 ...

For other uses, see Khidirpur (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kidderpore – news · newspapers · books · scholar · JSTOR (August 2008) (Learn how and when to remove this message) Neighbourhood in Kolkata in West Bengal, IndiaKidderporeNeighbourhood in Kolkata (Calcutta)Diamond...

Part of a series onSocialism HistoryOutline Development Age of the Enlightenment French Revolution Revolutions of 1848 Socialist calculation debate Socialist economics Ideas Calculation in kind Collective ownership Cooperative Common ownership Critique of political economy Economic democracy Economic planning Equal liberty Equal opportunity Free association Freed market Industrial democracy Input–output model Internationalism Labor-time calculation Labour voucher Material balance planning P...
Not to be confused with Pseudoathletic appearance which can include pseudohypertrophy, but also hypertrophy among other pathological forms of enlargement False enlargement of muscle due to infiltration of fat or other tissue Medical conditionPseudohypertrophyOther namesfalse enlargementDrawing of seven-year-old boy with Duchenne muscular dystrophy. There is pseudohypertrophy of the lower limbs.SymptomsWeaknessCausesmuscle disease, nerve disease Pseudohypertrophy, or false enlargement, is an i...

Bangunan di balik pepohonan tersebut merupakan bangunan awal G. Kolff & Co di Jakarta, yang pernah menjadi salah satu perusahaan penerbitan buku pertama dan paling sukses di Hindia Belanda. Bangunan tersebut ambruk pada 2015 dan kini telah dihancurkan. G. Kolff & Co., adalah sebuah perusahaan penerbitan, percetakan, dan toko buku yang berpusat di Batavia (sekarang Jakarta). Perusahaan ini adalah salah satu perusahaan penerbitan buku pertama yang dibuka di Batavia. Saingannya pada wakt...

French basketball player and coach André BuffièrePersonal informationBorn(1922-11-12)12 November 1922Vion, Ardèche, FranceDied2 October 2014(2014-10-02) (aged 91)Listed height6 ft 1 in (1.85 m)Listed weight190 lb (86 kg)Career informationPlaying career1945–1957PositionShooting guardCoaching career1948–1987Career historyAs player:1945–1947ESSMG Lyon1947–1948UA Marseille1948–1955ASVEL1955–1957ESSMG LyonAs coach:1948–1955ASVEL1955–1957SA Lyon1957�...
American herpetologist (1883–1968) Laurence Monroe KlauberLaurence M. Klauber, from A Century of Progress in the Natural Sciences (California Academy of Sciences, 1955)BornDecember 21, 1883San Diego, CaliforniaDiedMay 8, 1968(1968-05-08) (aged 84)San Diego, CaliforniaNationalityAmericanAlma materStanford UniversityScientific careerFieldsHerpetologyInstitutionsSan Diego Natural History Museum, San Diego Zoo Laurence Monroe Klauber (December 21, 1883, in San Diego, California – Ma...

Major American newspaper, founded 1847 The Trib redirects here. For other newspapers with similar names, see Tribune (disambiguation). Chicago TribuneThe March 24, 2024, front pageof the Chicago TribuneTypeDaily newspaperFormatBroadsheetOwner(s)Tribune PublishingFounder(s)James KellyJohn E. WheelerJoseph K. C. ForrestEditor-in-chiefMitch PughGeneral managerPar RidderOpinion editorChris JonesSports editorAmanda KaschubePhoto editorTodd PanagopoulosFoundedJune 10, 1847; 176 years a...

Deputy head of state and head of government of the Philippines For a list, see List of vice presidents of the Philippines. Vice President of of the Republic of the PhilippinesPangalawang Pangulo ng PilipinasVice presidential sealVice presidential flagIncumbentSara Dutertesince June 30, 2022Government of the PhilippinesOffice of the Vice PresidentStyle Madam Vice President(informal) The Honorable(formal) Her Excellency(diplomatic) StatusSecond highest executive branch officerMember ofCabi...

Disambiguazione – Se stai cercando altri significati, vedi 1989 (disambigua). XIX secolo · XX secolo · XXI secolo Anni 1960 · Anni 1970 · Anni 1980 · Anni 1990 · Anni 2000 1985 · 1986 · 1987 · 1988 · 1989 · 1990 · 1991 · 1992 · 1993 Il 1989 (MCMLXXXIX in numeri romani) è un anno del XX secolo. 1989 negli altri calendariCalendario gregoriano1989 Ab Urbe condita2742 (MMDCCXLII) Calendario armeno...

British films released in 1949 This film-related list is incomplete; you can help by adding missing items. (August 2008) Cinema of theUnited Kingdom List of British films British horror 1888–1919 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 19341935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 197...

Election in Connecticut Main article: 1880 United States presidential election 1880 United States presidential election in Connecticut ← 1876 November 2, 1880 1884 → Nominee James A. Garfield Winfield S. Hancock Party Republican Democratic Home state Ohio Pennsylvania Running mate Chester A. Arthur William H. English Electoral vote 6 0 Popular vote 67,071 64,411 Percentage 50.51% 48.50% County Results Garfield 40-50% 50-...

Azusa Iwashimizu Informasi pribadiNama lengkap Azusa IwashimizuTanggal lahir 14 Oktober 1986 (umur 37)Tempat lahir Prefektur Iwate, JepangPosisi bermain BekKarier senior*Tahun Tim Tampil (Gol)2003– Nippon TV Beleza 260 (21)Tim nasional2006–2016 Jepang 122 (11) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Azusa Iwashimizu (岩清水 梓, lahir 14 Oktober 1986) adalah seorang pemain sepak bola Jepang. Statistik [1][2] Jepang Tahun Tampil Gol 20...

Diese Liste umfasst die Schweizer Botschafter im Vereinigten Königreich. Inhaltsverzeichnis 1 Missionschefs 2 Siehe auch 3 Literatur 4 Weblinks 5 Einzelnachweise Missionschefs Schweizer Botschaft, 16-18 Montagu Place im Londoner Stadtteil Marylebone Schweiz Schweizer Botschafter in London[1] Name Amtsbeginn Amtsende Charles-Daniel Bourcart (1860–1940) – Generalkonsul 20. Februar 1891 7. Februar 1896 Charles-Daniel Bourcart (1860–1940) – Ministerresident 7. Februar 1896 21. De...

















![{\displaystyle [f(x)]'\quad f'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c165baa03042103d7f7b1dee3f7081569455545)












![{\displaystyle T^{*}u=\sum _{k=0}^{n}(-1)^{k}D^{k}[{\overline {a_{k}(x)}}u]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e24a2a49b70e9868143d33fc2df7aa5aef522309)


![{\displaystyle {\begin{aligned}L^{*}u&{}=(-1)^{2}D^{2}[(-p)u]+(-1)^{1}D[(-p')u]+(-1)^{0}(qu)\\&{}=-D^{2}(pu)+D(p'u)+qu\\&{}=-(pu)''+(p'u)'+qu\\&{}=-p''u-2p'u'-pu''+p''u+p'u'+qu\\&{}=-p'u'-pu''+qu\\&{}=-(pu')'+qu\\&{}=Lu\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f14429d10c7b73597f1f385bbb6d50c8b3517d9)




![{\displaystyle I=([D,X]-1)=(DX-XD-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcb338e5716e5dd19e6a7431bf4bff754c6e5d32)
![{\displaystyle I=\left({\begin{matrix}[D_{i},X_{j}]-\delta _{i,j},\\[2pt][D_{i},D_{j}],\\[2pt][X_{i},X_{j}]\end{matrix}}{\Bigg |}\;1\leq i,j\leq n\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99c4da7864ac40f8ef726b806cd40238d38d5c8c)




![{\displaystyle [f_{k},[f_{k-1},[\cdots [f_{0},P]\cdots ]]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0207e4c5239c7188b4bbe0a83388d1bb749a9918)
![{\displaystyle [f,P]\colon \Gamma (E)\to \Gamma (F)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b22f54c33f7efc45cebb514e5d23a5cbf94985e1)
=P(f\cdot s)-f\cdot P(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9417ee815b95cee52dd7f2728f5a9ca5624b999)