高階関数(こうかいかんすう、英: higher-order function)とは、第一級関数をサポートしているプログラミング言語において少なくとも以下のうち1つを満たす関数である。
概要
高階関数は厳密には第一級関数をサポートしているプログラミング言語において定義される。C言語やPascalでは、関数へのポインタを利用して高階関数を模倣することができるが、関数ポインタによって第一級関数をサポートしているとみなされてはいない。高階関数は主に関数型言語やその背景理論であるラムダ計算において多用される。
また、ある関数(手続き)の引数となる関数(手続き)のことを関数引数[1]や手続き引数[2]と呼ぶこともある。
種類
ここでは処理系に実装されていることが多いものだけをあげているが、高階関数も普通の関数と同様に、プログラマが自由に定義して利用できるということを特記しておく。
関数を呼び出す関数
以下に示す関数apply_2_3は、与えられた関数に引数2と3を渡して呼び出し、その返り値を返す高階関数である。関数定義であるために、f は評価はされても、式は呼び出されず、(apply_2_3 add) や (apply_2_3 mul) のように関数そのものを引数として渡して呼び出すことで評価される。
(define (add x y) (+ x y))
(define (mul x y) (* x y))
(define (apply_2_3 f) (f 2 3))
(apply_2_3 add) ; => (add 2 3) => 5
(apply_2_3 mul) ; => (mul 2 3) => 6
カリー化
複数の引数をとる関数を1変数関数に置き換えることをカリー化と呼ぶ。例えば二つの数を足し合わせる関数 add は以下のようになる。
; 通常の定義,呼び出し
(define (add x y) (+ x y))
(add 2 3) ;=> 5
; カリー化を施した定義,呼び出し
(define (add x) (lambda (y) (+ x y)))
((add 2) 3) ;=> 5
組み込みの関数が最初からカリー化されている言語がある。これは、関数呼び出しが常に1引数を取る関数を返すと定義するのと同じである(つまり n 引数関数を、n 個の引数の直積を取る関数とするのではなく、1 引数の高階関数を n 個並べたような型で定義する。)
例えば Haskell において、
と記述すると、これは先ほどの (add 2) と同じく、2を足す関数になる。関数 + が既にカリー化されているため、1 引数を適用するだけで関数として機能する。以下は実行例。
Prelude> 2 + 3
5
Prelude> (2 +) 3
5
filter
リスト中の各要素をおのおの引数として渡し、引数として渡された関数を呼び出し、その返り値が真なら返り値のリストに残し、偽なら排除される。排除したい要素に対して偽値を返す、述語のような役割の関数を与えて利用する。
例えば、リスト'(1 2 -3 -4 5)から、正の数のみを抽出するには以下のようにする[3]。
(filter positive? '(1 2 -3 -4 5))
;=> '(1 2 5)
zip
複数のリストからタプルを要素とする1つのリストを生成する。
(zip list1 list2 ... listn)
例えば、'(1 2 3)と'(a b c)に対してzipを行うと以下のようになる。
(zip '(1 2 3) '(a b c))
;=> '((1 a) (2 b) (3 c))
これは引数を再構成するのに便利だが、高階関数ではない。
unzip
zipの逆操作。タプルを要素とする1つのリストから複数のリストを生成する。
以下のように動作する:
(unzip '((1 a) (2 b) (3 c)))
;=> '(1 2 3) '(a b c)
ただし、実際には単一の戻り値しか返せない処理系・言語の場合、この戻り値のタプルとして返すことがある。その場合は以下のようになる。
(unzip '((a b c) (s t u) (x y z) (1 2 3)))
;=> ((a s x 1) (b t y 2) (c u z 3))
(unzip '((a s x 1) (b t y 2) (c u z 3)))
;=> ((a b c) (s t u) (x y z) (1 2 3))
これも引数の再構成に便利だが、高階関数ではない。
map
map関数はリスト構造の各要素に対して順々に与えられた関数を処理していくものである。関数プログラミングではないパラダイムの言語でも実装されていることがある。
(map func list0 list1 ... listN)
例えば、リスト'(1 2 3)の各要素に対して1を足したリストを得たい場合は以下のようにすれば良い。
(map (lambda (n) (+ 1 n)) '(1 2 3))
;=> '(2 3 4)
for-each
mapと同じように動くが、結果を返さない。つまり、出力など、副作用を期待して利用する。
fold
fold 関数は重畳(英語版)、堆積、畳み込みや折り畳みなどと呼ばれ、英語ではreduce、injectとも表現される。foldはリストの各要素に対して与えられた関数を適用する。
(fold func returns-first list)
例えば、リスト'(1 2 3)の各要素の総和を取るには以下のようにできる。
(fold + 0 '(1 2 3))
;=> 4
右方向の畳み込み(foldr)と左方向の畳み込み(foldl)があり、言語によっては最初から同様の機能が組み込まれていることがある(詳しくはfoldの英語版記事の該当項目を参照)。
![]()
(fold-right + 0 '(1 2 3))
;=> 6
; (+ 1 (+ 2 (+ 3 0)))と同じ
(fold-right cons '(0) '(1 2 3))
;=> '(1 2 3 0)
; (cons 1 (cons 2 (cons 3 '(0))))と同じ
|
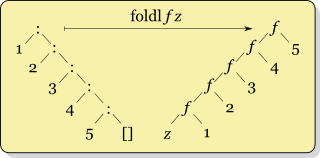
(fold-left + 0 '(1 2 3))
;=> 6
;(+ (+ (+ 0 1) 2 ) 3) と同じ
(fold-left cons '(0) '(1 2 3))
;=> '((((0) . 1) . 2) . 3)
;(cons (cons (cons '(0) 1) 2 ) 3) と同じ
|
unfold
foldの逆変換。すなわち初期値から何らかの動作を行なってリストを生成する関数である。例えるならば漸化式を数列に直す操作に相当する。
(unfold condition func iterate-update seed)
seedにfuncを適用しfuncの戻り値をリストへ格納し、seedをiterate-updateで更新してfuncを適用しfuncの戻り値をリストへ格納し、…といった操作をseedがconditionを真にするまで繰り返す。
例えば、要素4からリスト'(3 2 1)を生成するには、以下のようにする。
(unfold zero? (lambda(x)x) (lambda (n) (- n 1)) 3)
;=> '(3 2 1)
直積
複数のリストそれぞれを要素とするタプルを返す関数と見た時、直積集合を求める演算も高階関数と考えられる。R言語のouter関数などで実装されている。
prefix scan
prefix scan(英語版)(あるいは単にscan)とは、リストの各要素に対して繰り返し演算を行い累積した計算結果のリストを返す高階関数である。schemeでの実装例は以下のようになる[4]。
(define scan
(lambda (func seq)
(reverse
(fold-left
(lambda (l e) (cons (func e (car l)) l))
(list (car seq))
(cdr seq)))))
prefix scanの中で、特に和の演算はprefix sum, cumulative sumとも呼ばれる。ここでは先ほど定義したscanを使用して'(1 2 3 4 5 6 7 8 9 10)のprefix sumを求める例を示す。
(scan + '(1 2 3 4 5 6 7 8 9 10))
;=> '(1 3 6 10 15 21 28 36 45 55)
prefix scanは並列アルゴリズム、GPGPUの分野で研究される。またprefix sumの特殊系としてsegmented scan(英語版)もある。
関数型言語以外の言語と高階関数
関数型言語ではなくても、高階関数のような処理を行える場合がある。CやFortranにおける関数ポインタなどがその一例である。これらは言語にカリー化の機能やクロージャの機能がないという、制限はある。C#, C++, Tcl など、関数型言語でなくてもラムダ式がサポートされている言語は多い。
例えばCで関数を引数にとる関数を書くと次のようになる。
#include <assert.h>
/* int の二項演算 */
typedef int (*Function)(int, int);
/* 左結合 */
int foldl(int values[], int length, Function f, int identity_element) {
int folded = identity_element;
for (int i = 0; i < length; i++) {
folded = (*f)(folded, values[i]);
}
return folded;
}
/* 右結合 */
int foldr(int values[], int length, Function f, int identity_element) {
int folded = identity_element;
for (int i = length - 1; 0 <= i; i--) {
folded = (*f)(values[i], folded);
}
return folded;
}
/* 加算 */
int add(int x, int y) { return x + y; }
/* 乗算 */
int mul(int x, int y) { return x * y; }
/* 使用例 */
int main(void) {
int values[5] = {31, 4, 159, 26, 53};
int sum = foldl(values, sizeof values / sizeof(int), add, 0);
int product = foldl(values, sizeof values / sizeof(int), mul, 1);
assert(sum == 273);
assert(product == 27168648);
return 0;
}
一方、関数を戻り値とする関数を書くことは難しいため、クロージャを高階関数に渡すことができず、便利に使えない。高階関数が別の引数も受け付けるようにすれば、環境を閉じ込めることは不可能でないが、汎用性が低くなってしまう。
脚注
出典
- ^ 英: functional argument/parameter
- ^ 英: procedural argument/parameter
- ^ http://www.shido.info/lisp/scheme8.html
- ^ “Functional Programming - Implementing Scan (Prefix Sum) using Fold”. 2014年9月14日閲覧。
関連項目