射影極限
|
Read other articles:

Coordinate: 69°33′19″N 31°13′16″E / 69.555278°N 31.221111°E69.555278; 31.221111 Mappa della regione di Petsamo: la parte verde in alto è la penisola di Rybačij, ceduta all'Unione Sovietica dopo la guerra d'inverno; la parte chiara è la regione di Petsamo, acquisita dall'Unione Sovietica con i trattati di Parigi; la zona rossa è il territorio di Jäniskoski–Niskakoski, ceduto all'Unione Sovietica nel 1947 La regione di Petsamo, o Pečengskij rajon, (in ru...

العلاقات الأرجنتينية الطاجيكستانية الأرجنتين طاجيكستان الأرجنتين طاجيكستان تعديل مصدري - تعديل العلاقات الأرجنتينية الطاجيكستانية هي العلاقات الثنائية التي تجمع بين الأرجنتين وطاجيكستان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عا�...

Не следует путать со Сканер киноплёнки. Фильм-сканер «Nikon Coolscan II LS-20» с рамкой для негативов Фи́льм-ска́нер — телевизионный датчик, преобразующий изображение с фотографического негатива или диапозитива (слайда) в цифровой файл. От обычного планшетного сканера отличае...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Karnataka Chitrakala Parishath – news · newspapers · books · scholar · JSTOR (April 2018) (Learn how and when to remove this template message) Karnataka Chitrakala ParishathAbbreviationCKPFormation1960; 64 years ago (1960)FounderS. S. Kukke, M. Arya Murthy, M.S. Nanjunda RaoLocationBanga...

1912 ballet by Maurice Ravel This article is about the Fokine ballet to Ravel's music. For the original story, see Daphnis and Chloe. For the operetta by Jacques Offenbach, see Daphnis et Chloé (Offenbach). Daphnis et ChloéSet design by Léon Bakst for the world premiere of Daphnis et Chloé, Paris 1912.ChoreographerMichel FokineMusicMaurice RavelBased onLongus' Daphnis and ChloePremiere8 June 1912Théâtre du ChâteletParisOriginal ballet companyBallets RussesCharactersDaphnis, ChloéDesig...
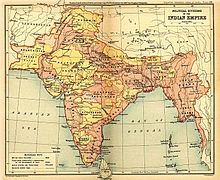
Historic treaty for princely states to join India or Pakistan This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Instrument of Accession – news · newspapers · books · scholar · JSTOR (August 2013) (Learn how and when to remove this message) The British Empire in the East, 1919: Princely states ...

Pour les articles homonymes, voir Attert. Cet article est une ébauche concernant une localité de la province de Luxembourg. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Attert Quartier de la vieille église Saint-Étienne Héraldique Drapeau Administration Pays Belgique Région Région wallonne Communauté Communauté française Province Province de Luxembourg Arrondissement Arlon Bourgmes...

Хип-хоп Направление популярная музыка Истоки фанкдискоэлектронная музыкадабритм-энд-блюзреггидэнсхоллджаз[1]чтение нараспев[англ.]исполнение поэзииустная поэзияозначиваниедюжины[англ.]гриотыскэтразговорный блюз Время и место возникновения Начало 1970-х, Бронкс, Н...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

Academy in Hexham, Northumberland, EnglandQueen Elizabeth High SchoolAddressWhetstone Bridge RoadHexham, Northumberland, NE46 3JBEnglandCoordinates54°58′12″N 2°07′04″W / 54.97012°N 2.11781°W / 54.97012; -2.11781InformationTypeAcademyMottoRespect. Engage. Aspire.Established1599; 425 years ago (1599)[1]FounderThomas StackhouseLocal authorityNorthumberlandTrustHadrian Learning TrustDepartment for Education URN143291 TablesOfstedRepor...

Albanian guide book Shqipria më 1927, e illustruar Book coverAuthorTeki SelenicaCountryAlbanian RepublicLanguageAlbanianGenreGuide bookPublished1928PublisherShtypshkronja TiranaPages330 Shqipria më 1927, e illustruar is a 1928 Albanian encyclopedic guide book authored by Teki Selenica.[1] Overview Teki Selenica was an Albanian government official known for having initiated and organized the registration of the first population census in the country. He published an encyclopedic guid...

国民阵线Barisan NasionalNational Frontباريسن ناسيونلபாரிசான் நேசனல்国民阵线标志简称国阵,BN主席阿末扎希总秘书赞比里署理主席莫哈末哈山总财政希山慕丁副主席魏家祥维纳斯瓦兰佐瑟古律创始人阿都拉萨成立1973年1月1日 (1973-01-01)[1]设立1974年7月1日 (1974-07-01)前身 联盟总部 马来西亚 吉隆坡 50480 秋傑区敦依斯迈路太子世贸中心(英�...

Daftar Jabatan Fungsional pada Pegawai Negeri Sipil ini disusun berdasarkan Peraturan Menteri Pendayagunaan Aparatur Negara dan Reformasi Birokrasi yang terdiri dengan 25 rumpun jabatan. Arikel ini mengelompokkan jabatan fungsional berdasarkan instansi pembina jabatan tersebut. Agendaː namaː nama jabatan fungsional Rumpunː rumpun jabatan Dasarː dasar hukum (PermenPAN-RB) Kementerian Dalam Negeri Nama Kategori Lingkup Rumpun Dasar Polisi Pamong Praja Keterampilan, Keahlian Daerah Penyidik ...
本文或本章節是關於未來的公共运输建設或計划。未有可靠来源的臆測內容可能會被移除,現時內容可能與竣工情況有所出入。 此条目讲述中国大陆處於施工或详细规划阶段的工程。设计阶段的資訊,或許与竣工后情況有所出入。无可靠来源供查证的猜测会被移除。 设想中的三条路线方案[1]。 臺灣海峽隧道或臺湾海峡橋隧(英語:Taiwan Strait Tunnel Project)是一项工程�...

Not to be confused with Water resources management in Guatemala or Irrigation in Guatemala. Guatemala: Water and Sanitation Data Access to an improved water source 92% (2010) [1] Access to improved sanitation 78% (2010) [1] Continuity of supply (%) not available Average urban water use (L/person/day) 125 Average domestic water tariff (US$/m3) 0.013 – 3.289[2] Share of household metering not available (low) Annual investment in water supply and sanitation US$1/person ...

2024 mixed martial event in Nevada, US UFC 306InformationPromotionUltimate Fighting ChampionshipDateSeptember 14, 2024 (2024-09-14)VenueSphereCityParadise, Nevada, United StatesEvent chronology UFC Fight Night 243 UFC 306 UFC Fight Night 244 UFC 306 (also known as Noche UFC 2) is an upcoming mixed martial arts event produced by the Ultimate Fighting Championship that will take place on September 14, 2024, at the Sphere in Paradise, Nevada, part of the Las Vegas Metropolitan Are...

1979 Italian filmThe Great Alligator RiverItalian theatrical release posterDirected bySergio MartinoProduced byLuciano MartinoCinematographyGiancarlo FerrandoMusic byStelvio CiprianiDistributed byMedusa DistribuzioneRelease date 3 November 1979 (1979-11-03) (Italy) Running time90 minutesCountryItalyLanguageItalian The Great Alligator River, originally Il fiume del grande caimano and also known as Alligators, Caiman, Big Alligator River and The Big Caimano River, is a 1979 I...

احتجاجات الحرب الفلسطينية الإسرائيلية في المملكة المتحدة وقفة تضامنية في كارديف، ويلز، رفضًا لقصف قطاع غزة (21 أكتوبر 2023) التاريخ 8 أكتوبر 2023 – الآن المكان المملكة المتحدة الأسباب الحرب الفلسطينية الإسرائيلية 2023 الأهداف متنوعة المظاهر الاحتجاجات، المظاهرات، عصيان مدني ت...

此條目需要补充更多来源。 (2018年9月6日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:TAKE FIVE~我们能盗取爱吗~ — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 TAKE FIVE~我们能盗取爱吗~TAKE FIVE〜俺たちは愛を盗めるか〜�...

For the Pennsylvania Quaker diarist (1758-1829), see Ann Warder. American novelist Ann HeadBornAnne Wales Christensen(1915-10-30)October 30, 1915Beaufort, South CarolinaDiedMay 7, 1968(1968-05-07) (aged 52)Beaufort, South CarolinaOccupationWriterGenreRomantic fictionmysteryyoung adultYears active1945–1967Notable worksMr. and Mrs. Bo Jo Jones Ann Head (née Anne Wales Christensen) (1915 – 1968) was an American fiction writer whose work was regularly published in magazines includi...




![{\displaystyle R[t]/t^{n+j}R[t]\to R[t]/t^{n}R[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d38ca7b8cab6419250ecf7139540414bb3691290)









