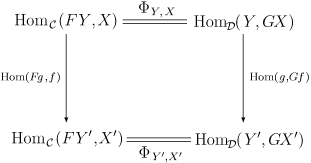æ°ćŠ ăźçčă«ćè« ă«ăăăé䌎 ïŒăăăŻăăè± : adjunction éąæ ăźéăźïŒăăçšźăźććŻŸ çăȘïŒéąäżăźăăšă§ăăïŒé䌎éąäżă«ăăéąæăæă€éąæăăăă°ăæăăȘăéąæăăăïŒăçŽæçă«èšăă°ăäșă€ăźçžäșă«éąéŁăăćăźéă«èȘăăăăăćŒ±ăćć€ çăȘéąäżăźăăšă§ăăăăăźéąäżăèĄšăéąæăźăăąăé䌎éąæăšćŒăłăçæčăć·Šé䌎ăăăçæčăćłé䌎ăšćŒă¶ăé䌎ăźæŠćż”ă»é䌎éąæăźăăąăŻæ°ćŠă«éćšăăæé©ćăćčçă«éąăăçŽèŠłçæŠćż”ăæăăă«ăăăŸăăăăçšźăźæ°ćŠçćéĄăź"è§Łæ±șæłăźæé©ć"ăèĄăéçšă§èŠćșăăă(代æ°ă«ăăăéćäžăźèȘç±çŸ€ ăźæ§æăăäœçžç©șéă«ăăăStoneâÄech compactification(è±èȘç )ăźæ§æăȘă©ăăăźäŸă§ăăă
ć
C
{\textstyle {\mathcal {C}}}
D
{\textstyle {\mathcal {D}}}
F
: : -->
D
→ â -->
C
,
G
: : -->
C
→ â -->
D
{\displaystyle F\colon {\mathcal {D}}\to {\mathcal {C}},\quad G\colon {\mathcal {C}}\to {\mathcal {D}}}
ăźćŻŸă§ăăŁăŠăć
C
{\textstyle {\mathcal {C}}}
X ăć
D
{\textstyle {\mathcal {D}}}
Y ă«ćŻŸăăŠăéćăźć
šćć°
hom
C
⥠-->
(
F
Y
,
X
)
≅ â
-->
hom
D
⥠-->
(
Y
,
G
X
)
{\displaystyle \operatorname {hom} _{\mathcal {C}}(FY,X)\cong \operatorname {hom} _{\mathcal {D}}(Y,GX)}
ăććšăăŠăăăă X ăš Y ă«ă€ăăŠèȘç¶ ăšăȘăăăźăèšăăăăźăšăăéąæ F ăć·Šé䌎ćœæ ăšćŒăłăä»æč G ăćłé䌎ćœæ ăšćŒă¶ăăŸăăăF 㯠G ăźć·Šé䌎ă§ăăă (ćăăăšă ăăăG 㯠F ăźćłé䌎ă§ăăă)ăšăăéąäżă
F
⊣ ⣠-->
G
{\displaystyle F\dashv G}
ăšæžăă
The slogan is “Adjoint functors arise everywhere.”
ăăźèšäșăźăăăăăźäŸ ă§ăŻăăæ°ćŠçæ§é ăźć€ăăé䌎éąæă§ăăăăšăć°ăă ăçŽčä»ăăă
ăăźăăšăŻăć·Š(ćł)é䌎éąæă«éąăăäžèŹçăȘćźçăăăšăă°èČă
ăȘćźçŸ©ăźăăăăźćć€æ§ăäœæ„”é(æ„”é) ăäżćăăăšăăćźç(ăăźăăšăŻæ°ćŠăźć
šăŠăźćéă§èŠă€ăă)ăăăć€ăăźćœčă«ç«ă€ă»éèȘæăȘç”æăć°ăăăšăćșæ„ăă
"adjunct"ăš"adjunction"ăš"adjoint"ăšăăăăă«ăäșă€ăźç°ăȘăèȘæ č ăäœżăăă(äŸăă°ăăăźèšäșăźè±èȘç)ăOxford shorter English dictionaryă«ăăăšă"adjunct"ăŻă©ăăłèȘç±æ„ă§ăăă"adjoint"ăŻăă©ăłăčèȘç±æ„ă§ăăă
Mac Lane è Categories for the working mathematician 珏4ç« "Adjoints" ă«ăăăŠăŻăæŹĄăźăăă«äœżăăăŠăăăźăçąșèȘă§ăăă
é䌎éąæăŻćçšźăźćéĄă«æ±șăŸăăăŁă æčæłăäœżăŁăŠăăŁăšăćčççăȘ è§Łăäžăăæčæłăšăăăăăăšăă°ăç°è« ăźćççăȘćéĄăšăăŠăéćäœçç° ăç°ă«ć€ăăćéĄăăăă
ăăŁăšăćčççă« èĄăă«ăŻă'1'ăèżœć ăăç°ăźć
Źçă§èŠæ±ăăăŠăăć
(ç°ăźćć
r ă«ćŻŸăăr +1ç)ăć
šăŠ(ăăăŠæć°éă)èżœć ăăć
ŹçăèŠæ±ăă仄äžăźéąäżăŻæăăȘăæ°ăăç°ăæ§æăăă°ăăăăăă«ăăăźæ§ææčæłăŻæŹèłȘçă«ăŻă©ăźéćäœçç°ă«ă€ăăŠăćăăăăăă«ăȘăă
ææ§ă«ăăŠç€șćçă§ăăăăćè«ăźèšèȘă«ăăŁăŠæŹĄăźăăă«ç°Ąæœă«èĄšçŸă§ăăă
ăæ§æăăăŁăšăćčçç ă§ăăăšăŻæźéçă§ăăăăšăæ±șăŸăăăŁă ăšăŻéąæăćźăăăăšăšăăăă ăăă§ăæźéçă§ăăăšăăăăšă«ăŻăć§ăæźéçăšăç”ăæźéçăź2ă€ăźçšźéĄăăăăăăăăŻććŻŸă§ăăăźă§ăçæčăźăżă«ă€ăăŠèăăă ăă§ććă§ăăă
ăć§ăăźć Žćăźæźéæ§ăšăŻăćéĄăèšèż°ă§ăăćE ăæșćăăŠăæ§æăăăăăźăE ăźć§ćŻŸè±Ą ă«ăȘăăăă«ăăăăšă§ăăăăăźæčæłăźć©çčăŻăäžé ăæ±ăăăăšăšćæ§ă«ăæé©ć (ăăă§ăŻăăăŁăšăćčççăȘ è§ŁăèŠă€ăăăăš)ăæŁçąșăȘç”æăäžăăèȘèăăăăăăšă«ăăăæŁăăE ăéžă¶ă«ăŻć°ăăă€ăăăăăăšăă°ăćäœçă§ăȘăç°R ăăăŁăć Žćă«ăćE ăźćŻŸè±ĄăŻéćäœçç°ăźæșćć R â S ă§ăăŁăŠăS ăäčæłçćäœć
ăăă€ăăźă§ăăăăăćŻŸè±Ą R â S1 ăš ćŻŸè±ĄR â S2 ăźéăźć°ăŻäžè§ćŻæćłćŒ (R â S1 ,R â S2 , S1 â S2 )ăźăăĄăS1 â S2 ăćäœć
ăäżćăăç°ăźæșććă«ăȘăŁăŠăăăšăăăćŻŸè±Ą R â S1 ăš ćŻŸè±ĄR â S2 ăźéă«ć°ăććšăăăšăăăăšăŻăS1 ăŻć°ăȘăăšă S2 ăăăăăćčççăȘ è§Łă§ăăăăšăç€șăăŠăăăăăȘăăĄăS2 㯠S1 ăăăć€ăăźć
ăæăŁăŠăăăăć
Źçă«ăȘăéąäżăæșăăăăšăćŻèœă§ăăăăăŁăŠăR â R* ă E ăźć§ćŻŸè±Ąă§ăăăšăăăăšăŻăć§ćŻŸè±ĄăăăŻE ăźä»ăźă©ăźćŻŸè±Ąăžăć°ăććšăăăšăăăăšăăăR* ăŻăăŁăšăćčççăȘ è§Łă§ăăăăšăăăăă
éćäœçç°ăç°ă«ć€ăăăăźæčæłăăăŁăšăćčçç ă§æ±șăŸăăăŁă æčæłă§ăăăšăăăăšăăăăźæčæłăé䌎éąæ ăćźăăŠăăăšäžèšă§èĄšçŸăăăăšăă§ăăă
æŹĄă«ăéąæF ăăć§ăă ć Žćă§ăŻăF ăăăŁăšăćčççăȘè§ŁăšăȘăćéĄăŻććšăăăźăïŒăăšăă(ææ§ăȘ)èłȘćăćŻèœă§ăăă
F ăG ćéĄăźăăŁăšăćčççăȘè§Ł ă§ăăăšăăăăšăŻăăăæćłă§ăŻæŁçąșă«ăG ăF ăè§ŁăšăȘăăăŁăšăéŁăăćéĄ ă§ăăăăšăšćć€ăšăȘăă[èŠćșć
ž
ăăăé䌎éąæăćŻŸăšăȘăŁăŠçŸăăăăšăźçŽèŠłçăȘè§Łéă§ăăăćźéăăăŻæŁăăăăæźéć°ăäœżăŁăćźçŸ©ă§ăŻèȘæă§ăŻăȘăăé䌎éąæăçšăăćŻŸç§°ćœąăźé䌎ăźćźçŸ©(F ăŻG ăźć·Šé䌎ă§ăăăšèšăŁăŠăăăăăG ăŻF ăźćłé䌎ă§ăăăšèšăŁăŠăăă)ăäœżăăăšă§ăăăźăăšăæç€șçă«ăȘăăšăăć©çčăăăă
é䌎éąæăźćźçŸ©ăŻăăŸăăŸăȘæčæłăăăăăăăăźćć€æ§ăŻćșæŹçăȘäșćźă§ăăăèȘæă§ăŻăȘăăăéćžžă«æçšă§ăăăăăźèšäșă§ăŻăăă€ăăźćźçŸ©ăäžăăă
æźéć°ăçšăăćźçŸ©ăŻæžăăźăç°Ąćă§ăé䌎éąæăæ§æăăăăé䌎ă§ăăăăšă蚌æăăć Žćă«ćż
èŠăȘæ€èšŒé
çźăć°ăȘăăæé©ćă«ćŻŸăăçŽèŠłă«ăăŁăšăèżăæčæłă§ăăă
äœćäœ-ćäœé䌎ăçšăăćźçŸ©ăŻé䌎éąæă§ăăăăšăćăăŁăŠăăéąæă«éąäżăă蚌æăæžăăźă«äŸżć©ă§ăăăăȘăăȘăăçŽæ„æäœă§ăăć
ŹćŒăæă€ăăă§ăăă
homéćăçšăăćźçŸ©ăŻăăŁăšăćŻŸç§°æ§ăăăăăăăăăăăé䌎 ăšăăćèȘăäœżăçç±ă§ăăă é䌎éąæăŻæ°ćŠăźć
šăŠăźćéă«çŸăăăăăăăźćźçŸ©ăæă€æ§é ăä»ăźćźçŸ©ăæă€æ§é ă«æăĄäžăăăăă«ăŻé·ăăæăăăȘ蚌æăćż
èŠă§ăăăăăźăăšăé䌎ăćźć
šă«æçšăȘăăźă«ăăŠăăăé䌎ăźććźçŸ©ăèĄăäș€ăăăšăŻăććéă§çč°ăèżăèĄăăăŠăăéć±ăȘéšćăæé»ă«äœżăŁăŠăăăăšă«ăȘăăäŸăă°counităç”ćŻŸè±Ąă§ăăèȘç¶ă§ăăăăšăăć
šăŠăźćłé䌎éąæăæ„”éăäżćăăăăšă蚌æă§ăăă
é䌎ăźçè«ăŻćșç€ä»ăă«ăć·ŠăăšăćłăăšăăèšèăçšăăăŸăèăăăčăäșă€ăźć đ ăš đ ăźäžă«ăŻăăăăăźæ§æèŠçŽ ăććšăăŠăăăăăă§ăăć·Šăăźć đ ăăăšăŁăăźăăćłăăźć đ ăăćăŁăăźăăăăăźć·Šăćłăźé ă§ä»ăăæćăăąă«ăăĄăăăé ăšăȘăăăă«ăăăŸăă§ăăăéăăăźé ă§æžăäžăăăă«ăăăšéćžžă«äŸżć©ă§ăăă
ăăźèšäșă§ăŻäŸăă°ăX ăF ăf ăΔ ăŻćC ăăăY ăG ăg ăη ăŻćD ăăćăŁăŠăăăăźăšăăăăăăŠăćŻèœăȘć ŽćăŻăăăźé ă§ć·Šăăćłă«äœżăăăšăźăă(äŸăă°ăéąæ F :C âD ăŻC ăăćăŁăŠăăăăźăšèăă)
éąæ F : C â D ăć·Šé䌎éąæ ă§ăăăšăŻăC ăźććŻŸè±ĄX ă«ćŻŸăăŠăF ăăX ăžăźæźéć° ăććšăăăăšă§ăăăC ăźććŻŸè±ĄX ă«éąăăŠD ăźćŻŸè±ĄG 0 X ăšF ăăX ăžăźæźéć°Î”X F (G 0 X ) â X ăæ±șăăăšăéąæG : C â D ă§ăGX = G 0 X ăšăä»»æăźC ăźć°f : X â XÊč ă«ă€ăăŠÎ”XÊč
∘ â -->
{\displaystyle \circ }
FG (f ) = f
∘ â -->
{\displaystyle \circ }
X F ăŻG ăźć·Šé䌎 ă§ăăăšăăă
éąæ G : C â D ăćłé䌎éąæ ă§ăăăšăŻăD ăźććŻŸè±ĄY ă«ćŻŸăăŠăY ăăG ăžăźæźéć°ăććšăăăăšă§ăăăD ăźććŻŸè±ĄY ă«éąăăŠC ăźćŻŸè±ĄF 0 Y ăšY ăăG ăžăźæźéć°Î·Y Y â G (F 0 Y )ăæ±șăăăšăéąæF : C â D ă§ăFY = F 0 Y ăšăä»»æăźD ăźć°g : Y â YÊč ă«ă€ăăŠGF (g )
∘ â -->
{\displaystyle \circ }
Y YÊč
∘ â -->
{\displaystyle \circ }
g ăæăç«ă€ăăźăäžæçă«ććšăăăăăźăšăăG ăŻF ăźćłé䌎 ă§ăăăšăăă
æłšæ
çšèȘăăćăăăăă«ăF ăGăźć·Šé䌎 ă§ăăăăšăšG ăFăźćłé䌎 ă§ăăăăšăćć€ă§ăăăăšăŻæŁăăăăăăŻäžèšăźćŻŸç§°çăȘćźçŸ©ă§ăŻæăăă§ăăăæźéć°ăçšăăćźçŸ©ăŻăäžăăăăéąæăć·ŠăŸăăŻćłé䌎éąæă§ăăăăšă ăăçąșăăăăăšăă«ăćż
èŠăȘ蚌æăæć°éăšăȘăăăăăă°ăă°æçšă§ăăăăŸăăæźéć°ăæ±ăăăăšăŻæé©ććéĄăè§ŁăăăšăšäŒŒăŠăăăăăçŽèŠłçă§ăăăă
ćC ăšD ăźäœćäœ-ćäœé䌎 ăŻ2ă€ăźéąæ F : C â D ăš G : C â D ăăăł2ă€ăźèȘç¶ć€æïŒăăăăăăăźé䌎ăźäœćäœć°ăăăłćäœć°ăšćŒă°ăăïŒ
ε Δ -->
: : -->
F
G
→ â -->
1
C
η η -->
: : -->
1
D
→ â -->
G
F
{\displaystyle {\begin{aligned}\varepsilon \colon &FG\to 1_{\mathcal {C}}\\\eta \colon &1_{\mathcal {D}}\to GF\end{aligned}}}
ă§ăăŁăŠăăăăăźćæ
F
→
F
η η -->
F
G
F
→
ε Δ -->
F
F
{\displaystyle F{\xrightarrow {\;F\eta \;}}FGF{\xrightarrow {\;\varepsilon F\,}}F}
G
→
η η -->
G
G
F
G
→
G
ε Δ -->
G
{\displaystyle G{\xrightarrow {\;\eta G\;}}GFG{\xrightarrow {\;G\varepsilon \,}}G}
ăăăăăăF ăšG äžăźæçć€æ1F G counit ăšunit ăšćŒă¶ă
ăăźăšăă F ăŻG ăźć·Šé䌎 ă§ăă G ăŻF ăźćłé䌎 ă§ăăăšăăăăăźéąäżă
(
ε Δ -->
,
η η -->
)
:
F
⊣ ⣠-->
G
{\displaystyle (\varepsilon ,\eta ):F\dashv G}
F
⊣ ⣠-->
G
{\displaystyle F\dashv G}
(Δ,η)ă«éąăăäžăźæĄä»¶ăçćŒă§æžăăšăcounit-unitæçćŒ ăšćŒă°ăă
1
F
=
ε Δ -->
F
∘ â -->
F
η η -->
1
G
=
G
ε Δ -->
∘ â -->
η η -->
G
{\displaystyle {\begin{aligned}1_{F}&=\varepsilon F\circ F\eta \\1_{G}&=G\varepsilon \circ \eta G\end{aligned}}}
ăšăȘăăăăăŻC ăźććŻŸè±ĄX ăšD ăźććŻŸè±ĄY ă«ă€ăăŠ
1
F
Y
=
ε Δ -->
F
Y
∘ â -->
F
(
η η -->
Y
)
1
G
X
=
G
(
ε Δ -->
X
)
∘ â -->
η η -->
G
X
{\displaystyle {\begin{aligned}1_{FY}&=\varepsilon _{FY}\circ F(\eta _{Y})\\1_{GX}&=G(\varepsilon _{X})\circ \eta _{GX}\end{aligned}}}
ăæăç«ă€ăăšăæćłăăă
ăăăăźçćŒăŻé䌎éąæă代æ°çă«æäœăă蚌æăçăăăăźă«æçšă§ăăăćŻŸćżăăstring diaglam ă§ăźèŠăçźăăăăăăŻăšăă«ăžă°ă¶ă°æçćŒ ăšćŒă°ăăăăăźçćŒăèŠăăă«ăŻăăŸăăçĄæćłăȘçćŒ
1
=
ε Δ -->
∘ â -->
η η -->
{\displaystyle 1=\varepsilon \circ \eta }
F ăšG ăèżœć ăăă°ăăă
æłš: ăăă§ăźcounităź"co"ăšăăæ„é èŸăŻæ„”é(limit)ăäœæ„”é(colimit)ă§ăźçšæłăšăŻäžèČ«ăăŠăăȘăăăȘăăȘăăäœæ„”éăŻăć§ăæźéæ§ăæșăăăźă«ćŻŸăăcounităźćźăăć°ăŻăç”ăæźéæ§ăæșăăăăă§ăăăăăăăźććŻŸă«ă€ăăŠăćæ§ă§ăăăăăă§ăźunit ăšăăçšèȘăŻăąăă ăăăźćçšă§ăăăæçć°1ăăąăă€ăă«ćă蟌ăăšăăăăæ„ăŠăăă
ćC ăšD ăźéăźhoméćăźé䌎 ăŻ2ă€ăźéąæ F : C â D ăš G : C â D ăăăłăèȘç¶ćć
Φ ÎŠ -->
:
h
o
m
C
(
F
− â -->
,
− â -->
)
→ â -->
h
o
m
D
(
− â -->
,
G
− â -->
)
{\displaystyle \Phi :\mathrm {hom} _{C}(F-,-)\to \mathrm {hom} _{D}(-,G-)}
ăźăăšăăăăăăăŻC ăźććŻŸè±ĄX ăšD ăźććŻŸè±ĄY ă§æ·»ăćä»ăăăăć
šćć°ăźæ
Φ ÎŠ -->
Y
,
X
:
h
o
m
C
(
F
Y
,
X
)
→ â -->
h
o
m
D
(
Y
,
G
X
)
{\displaystyle \Phi _{Y,X}:\mathrm {hom} _{C}(FY,X)\to \mathrm {hom} _{D}(Y,GX)}
ăćźăăă
ăăźăšăă F ăŻG ăźć·Šé䌎 ă§ăă G ăŻF ăźćłé䌎 ă§ăăăšăăăăăźéąäżă
Φ ÎŠ -->
:
F
⊣ ⣠-->
G
{\displaystyle \Phi :F\dashv G}
F
⊣ ⣠-->
G
{\displaystyle F\dashv G}
ăăźćźçŸ©ăŻæźéć°ăäœżăŁăăăźăăć°ăçąșèȘăăăăšăć€ăăŠăăăă«ćŸăăăç”æăŻäœćäœ-ćäœé䌎ăăć°ăȘăăȘăăšăăè«ççăȘæèĄ·ă«ăȘăŁăŠăăăæăăăȘćŻŸç§°æ§ăä»ăźćźçŸ©ăźéăźæ¶ăæ©ă«ăăăšăŻæçšă§ăăă
ΊăèȘç¶ććă§ăăăšăăăšăăŻăhomC F â, â) ăš homD G â) ăéąæă§ăăăšèăăćż
èŠăăăăćźéăăăăăŻD op Ă C ăăSet (éćăźć )ăžăźćéąæă§ăăăè©łăăăŻHoméąæ ăźé
çźăćç
§ăăăæç€șçă«æžăăšăΊăźèȘç¶æ§ăšăăăźăŻăć
šăŠăźC ăźć° f : X â XâČ ăšć
šăŠăźD ăźć°g : YâČ â Y ă«ă€ăăŠă仄äžăźćłćŒăćŻæă«ăȘăăăšăăăă
Naturality of Ί ăăźćłćŒăźçžŠæčćăźć°ăŻf ăg ăćæăăăăšă§èȘć°ăăăć°ă§ăăă
仄äžăźăăšăăăé䌎ă«ăŻăăăăăźéąæăèȘç¶ć€æăæăŁăŠăăăăăăźäžéšăæ±șăăă ăă§ä»ăźăăźăŻæ±șćźăăăă
ćC ăšD ăźéăźé䌎ăŻä»„äžăźăăźăăæ§æăăăă
ć·Šé䌎 ăšćŒă°ăăéąæF : C â D ćłé䌎 ăšćŒă°ăăéąæG : C â D èȘç¶ććΊ : homC F â,â) â homD G â)
äœćäœ ăšćŒă°ăăèȘç¶ć€æ Δ : FG â 1C ćäœ ăšćŒă°ăăèȘç¶ć€æ η : 1D GF çäŸĄăȘćźćŒćăšăăŠăX ăC ăźä»»æăźćŻŸè±ĄăšăY ăD ăźä»»æăźćŻŸè±Ąăšăăăšăă
ć
šăŠăź Căźć°
f
:
F
Y
→ â -->
X
{\displaystyle f:FY\to X}
Dăźć°
Φ ÎŠ -->
Y
,
X
(
f
)
=
g
:
Y
→ â -->
G
X
{\displaystyle \Phi _{Y,X}(f)=g:Y\to GX}
Dăźć°
g
:
Y
→ â -->
G
X
{\displaystyle g:Y\to GX}
Căźć°
Φ ÎŠ -->
Y
,
X
− â -->
1
(
g
)
=
f
:
F
Y
→ â -->
X
{\displaystyle \Phi _{Y,X}^{-1}(g)=f:FY\to X}
ăăźăăšăäœżăăšă仄äžă«æăăćŸ©ć
ăćŻèœă§ăă
ć€æΔăηăΊăŻä»„äžăźçćŒă§éąéŁä»ăăăăă
f
=
Φ ÎŠ -->
Y
,
X
− â -->
1
(
g
)
=
ε Δ -->
X
∘ â -->
F
(
g
)
∈ â -->
h
o
m
C
(
F
(
Y
)
,
X
)
g
=
Φ ÎŠ -->
Y
,
X
(
f
)
=
G
(
f
)
∘ â -->
η η -->
Y
∈ â -->
h
o
m
D
(
Y
,
G
(
X
)
)
Φ ÎŠ -->
G
X
,
X
− â -->
1
(
1
G
X
)
=
ε Δ -->
X
∈ â -->
h
o
m
C
(
F
G
(
X
)
,
X
)
Φ ÎŠ -->
Y
,
F
Y
(
1
F
Y
)
=
η η -->
Y
∈ â -->
h
o
m
D
(
Y
,
G
F
(
Y
)
)
{\displaystyle {\begin{aligned}f=\Phi _{Y,X}^{-1}(g)&=\varepsilon _{X}\circ F(g)&\in &\,\,\mathrm {hom} _{C}(F(Y),X)\\g=\Phi _{Y,X}(f)&=G(f)\circ \eta _{Y}&\in &\,\,\mathrm {hom} _{D}(Y,G(X))\\\Phi _{GX,X}^{-1}(1_{GX})&=\varepsilon _{X}&\in &\,\,\mathrm {hom} _{C}(FG(X),X)\\\Phi _{Y,FY}(1_{FY})&=\eta _{Y}&\in &\,\,\mathrm {hom} _{D}(Y,GF(Y))\\\end{aligned}}}
ć€æΔăηăŻäœćäœ-ćäœæçćŒăæșăă
1
F
=
ε Δ -->
F
∘ â -->
F
η η -->
1
G
=
G
ε Δ -->
∘ â -->
η η -->
G
{\displaystyle {\begin{aligned}1_{F}&=\varepsilon F\circ F\eta \\1_{G}&=G\varepsilon \circ \eta G\end{aligned}}}
C ă«ăăăŠăććŻŸ
(
G
X
,
ε Δ -->
X
)
{\displaystyle (GX,\varepsilon _{X})}
F ăăX ăžăźæźéć°ă§ăăD ă«ăăăŠăććŻŸ
(
F
Y
,
η η -->
Y
)
{\displaystyle (FY,\eta _{Y})}
Y ăăG ăžăźæźéć°ă§ăăăšăă«ăäžèšăźçćŒă«ăăΊăΔăηăŻăăăăźăăĄ1ă€ăäœżăŁăŠćźăăăăšăă§ăăăăăăăé䌎éąæF ăšG ă ăă§ăŻé䌎ăćźăăă«ăŻäžèŹă«ăŻććă§ăŻăȘăă仄äžă§ăŻćźçŸ©ăźćć€æ§ăè§ŁèȘŹăăă
æźéć°ăźæćłă§ăźćłé䌎éąæ
G
:
C
→ â -->
D
{\displaystyle G:C\to D}
éąæ
F
:
C
← â -->
D
{\displaystyle F:C\gets D}
η η -->
{\displaystyle \eta }
D ăźććŻŸè±ĄY ă«ćŻŸăăŠăY ăăG ăžăźæźéć°
(
F
(
Y
)
,
η η -->
Y
)
{\displaystyle (F(Y),\eta _{Y})}
η η -->
Y
:
Y
→ â -->
G
(
F
(
Y
)
)
{\displaystyle \eta _{Y}:Y\to G(F(Y))}
F ăšć°ăźæ
η η -->
{\displaystyle \eta }
ćć°
f
:
Y
0
→ â -->
Y
1
{\displaystyle f:Y_{0}\to Y_{1}}
(
F
(
Y
0
)
,
η η -->
Y
0
)
{\displaystyle (F(Y_{0}),\eta _{Y_{0}})}
η η -->
Y
0
{\displaystyle \eta _{Y_{0}}}
η η -->
Y
1
∘ â -->
f
{\displaystyle \eta _{Y_{1}}\circ f}
F
(
f
)
:
F
(
Y
0
)
→ â -->
F
(
Y
1
)
{\displaystyle F(f):F(Y_{0})\to F(Y_{1})}
F ăźć°éąæ°ă§ăă
ćè§Łă«ă€ăăŠăźćŻæćłćŒăăèȘç¶ć€æăšăăŠăźćŻæćłćŒăćŸăăăăăăŁăŠă
η η -->
:
1
D
→ â -->
G
∘ â -->
F
{\displaystyle \eta :1_{D}\to G\circ F}
ćè§Łăźäžææ§ăšG ăéąæă§ăăăăšăăăF ăźć°éąæ°ăć°ăźćæăšæçć°ăäżćăăăăšăăăă
èȘç¶ćć
Φ ÎŠ -->
:
h
o
m
C
(
F
− â -->
,
− â -->
)
→ â -->
h
o
m
D
(
− â -->
,
G
− â -->
)
{\displaystyle \Phi :\mathrm {hom} _{C}(F-,-)\to \mathrm {hom} _{D}(-,G-)}
C ăźććŻŸè±ĄX ăšD ăźććŻŸè±ĄY ă«ćŻŸăăŠă
(
F
(
Y
)
,
η η -->
Y
)
{\displaystyle (F(Y),\eta _{Y})}
Φ ÎŠ -->
Y
,
X
{\displaystyle \Phi _{Y,X}}
Φ ÎŠ -->
Y
,
X
(
f
:
F
(
Y
)
→ â -->
X
)
=
G
(
f
)
∘ â -->
η η -->
Y
{\displaystyle \Phi _{Y,X}(f:F(Y)\to X)=G(f)\circ \eta _{Y}}
η η -->
{\displaystyle \eta }
G ăéąæă§ăăăăšăăăć
šăŠăźC ăźćŻŸè±Ą
X
0
{\displaystyle X_{0}}
X
1
{\displaystyle X_{1}}
D ăźćŻŸè±Ą
Y
0
{\displaystyle Y_{0}}
Y
1
{\displaystyle Y_{1}}
x
:
X
0
→ â -->
X
1
{\displaystyle x:X_{0}\to X_{1}}
y
:
Y
1
→ â -->
Y
0
{\displaystyle y:Y_{1}\to Y_{0}}
Φ ÎŠ -->
Y
1
,
X
1
(
x
∘ â -->
f
∘ â -->
F
(
y
)
)
=
G
(
x
)
∘ â -->
G
(
f
)
∘ â -->
G
(
F
(
y
)
)
∘ â -->
η η -->
Y
1
=
G
(
x
)
∘ â -->
G
(
f
)
∘ â -->
η η -->
Y
0
∘ â -->
y
=
G
(
x
)
∘ â -->
Φ ÎŠ -->
Y
0
,
X
0
(
f
)
∘ â -->
y
{\displaystyle \Phi _{Y_{1},X_{1}}(x\circ f\circ F(y))=G(x)\circ G(f)\circ G(F(y))\circ \eta _{Y_{1}}=G(x)\circ G(f)\circ \eta _{Y_{0}}\circ y=G(x)\circ \Phi _{Y_{0},X_{0}}(f)\circ y}
ćæ§ăźè°è«ă«ăăæźéć°ă«ăăć·Šé䌎éąæăźćźçŸ©ăăhoméćăźé䌎ăæ§æăăăăšăă§ăăă(ćłé䌎ăć
ă«æ§æăăă»ăăæźéă§ăăăăȘăăȘăăéäŒŽćŻŸăźćłé䌎ăć
ć«éąæăćżćŽéąæă«ăăèȘæăȘăăæčă§ćźăăăăšăć€ăăăăăă§ăăă)
éąæ
F
: : -->
C
← â -->
D
{\displaystyle F\colon C\leftarrow D}
G
: : -->
C
→ â -->
D
{\displaystyle G\colon C\to D}
(
ε Δ -->
,
η η -->
)
: : -->
F
⊣ ⣠-->
G
{\displaystyle (\varepsilon ,\eta )\colon F\dashv G}
Φ ÎŠ -->
: : -->
h
o
m
C
(
F
− â -->
,
− â -->
)
→ â -->
h
o
m
D
(
− â -->
,
G
− â -->
)
{\displaystyle \Phi \colon \mathrm {hom} _{C}(F-,-)\to \mathrm {hom} _{D}(-,G-)}
ă仄äžăźæé ă§æ§æăăă
ć°
f
: : -->
F
Y
→ â -->
X
{\displaystyle f\colon FY\to X}
g
: : -->
Y
→ â -->
G
X
{\displaystyle g\colon Y\to GX}
Φ ÎŠ -->
Y
,
X
(
f
)
=
G
(
f
)
∘ â -->
η η -->
Y
Ψ Îš -->
Y
,
X
(
g
)
=
ε Δ -->
X
∘ â -->
F
(
g
)
{\displaystyle {\begin{aligned}\Phi _{Y,X}(f)=G(f)\circ \eta _{Y}\\\Psi _{Y,X}(g)=\varepsilon _{X}\circ F(g)\end{aligned}}}
ăšćźăăăšăηăšÎ”ăèȘç¶ă§ăăăăăΊăšÎšăèȘç¶ă§ăăă F ăéąæă§ăăăăšăšăΔăèȘç¶ă§ăăăăšcounit-unitæçćŒ
1
F
Y
=
ε Δ -->
F
Y
∘ â -->
F
(
η η -->
Y
)
{\displaystyle 1_{FY}=\varepsilon _{FY}\circ F(\eta _{Y})}
Ψ Îš -->
Φ ÎŠ -->
f
=
ε Δ -->
X
∘ â -->
F
G
(
f
)
∘ â -->
F
(
η η -->
Y
)
=
f
∘ â -->
ε Δ -->
F
Y
∘ â -->
F
(
η η -->
Y
)
=
f
∘ â -->
1
F
Y
=
f
{\displaystyle {\begin{aligned}\Psi \Phi f&=\varepsilon _{X}\circ FG(f)\circ F(\eta _{Y})\\&=f\circ \varepsilon _{FY}\circ F(\eta _{Y})\\&=f\circ 1_{FY}=f\end{aligned}}}
ăćŸăăăăŁăŠăΚΊăŻæçć€æă§ăă ććŻŸçă«ăG ăéąæă§ăăăăšăηăèȘç¶ă§ăăăăšcounit-unitæçćŒ
1
G
X
=
G
(
ε Δ -->
X
)
∘ â -->
η η -->
G
X
{\displaystyle 1_{GX}=G(\varepsilon _{X})\circ \eta _{GX}}
Φ ÎŠ -->
Ψ Îš -->
g
=
G
(
ε Δ -->
X
)
∘ â -->
G
F
(
g
)
∘ â -->
η η -->
Y
=
G
(
ε Δ -->
X
)
∘ â -->
η η -->
G
X
∘ â -->
g
=
1
G
X
∘ â -->
g
=
g
{\displaystyle {\begin{aligned}\Phi \Psi g&=G(\varepsilon _{X})\circ GF(g)\circ \eta _{Y}\\&=G(\varepsilon _{X})\circ \eta _{GX}\circ g\\&=1_{GX}\circ g=g\end{aligned}}}
ăćŸăăăăŁăŠăΊΚăŻæçć€æă§ăăăΊâ1 = ΚăéććăšăăŠÎŠăŻèȘç¶ććăšăȘăă
éąæ
F
: : -->
C
← â -->
D
{\displaystyle F\colon C\leftarrow D}
G
: : -->
C
→ â -->
D
{\displaystyle G\colon C\to D}
Φ ÎŠ -->
: : -->
h
o
m
C
(
F
− â -->
,
− â -->
)
→ â -->
h
o
m
D
(
− â -->
,
G
− â -->
)
{\displaystyle \Phi \colon \mathrm {hom} _{C}(F-,-)\to \mathrm {hom} _{D}(-,G-)}
(
ε Δ -->
,
η η -->
)
: : -->
F
⊣ ⣠-->
G
{\displaystyle (\varepsilon ,\eta )\colon F\dashv G}
ă仄äžăźæé ă§æ§æăăă
C ăźććŻŸè±ĄX ă«ćŻŸăăŠă
ε Δ -->
X
=
Φ ÎŠ -->
G
X
,
X
− â -->
1
(
1
G
X
)
∈ â -->
h
o
m
C
(
F
G
X
,
X
)
{\displaystyle \varepsilon _{X}=\Phi _{GX,X}^{-1}(1_{GX})\in \mathrm {hom} _{C}(FGX,X)}
1
G
X
∈ â -->
h
o
m
D
(
G
X
,
G
X
)
{\displaystyle 1_{GX}\in \mathrm {hom} _{D}(GX,GX)}
D ăźććŻŸè±ĄY ă«ćŻŸăăŠă
η η -->
Y
=
Φ ÎŠ -->
Y
,
F
Y
(
1
F
Y
)
∈ â -->
h
o
m
D
(
Y
,
G
F
Y
)
{\displaystyle \eta _{Y}=\Phi _{Y,FY}(1_{FY})\in \mathrm {hom} _{D}(Y,GFY)}
1
F
Y
∈ â -->
h
o
m
C
(
F
Y
,
F
Y
)
{\displaystyle 1_{FY}\in \mathrm {hom} _{C}(FY,FY)}
Ίăć
šćć°ă§èȘç¶ă§ăăăăšăăăć
(
G
X
,
ε Δ -->
X
)
{\displaystyle (GX,\varepsilon _{X})}
F ăăX ăžăźæźéć°ă§ăăăć
(
F
Y
,
η η -->
Y
)
{\displaystyle (FY,\eta _{Y})}
Y ăăG ăžăźæźéć°ă§ăăă
ΊăèȘç¶ă§ăăăăšăăăΔăšÎ·ăźæźéæ§ăć°ăăăćć° f : FY â X ăš g : Y â GX ă«ćŻŸăăŠă2ă€ăźć
ŹćŒ
Φ ÎŠ -->
Y
,
X
(
f
)
=
G
(
f
)
∘ â -->
η η -->
Y
Φ ÎŠ -->
Y
,
X
− â -->
1
(
g
)
=
ε Δ -->
X
∘ â -->
F
(
g
)
{\displaystyle {\begin{aligned}\Phi _{Y,X}(f)=G(f)\circ \eta _{Y}\\\Phi _{Y,X}^{-1}(g)=\varepsilon _{X}\circ F(g)\end{aligned}}}
ăæç«ăă(ăăăŻÎŠăćźć
šă«æ±șćźăă) äșçȘçźăźć
ŹćŒăźX ă«FY ă代ć
„ăăg ă«
η η -->
Y
=
Φ ÎŠ -->
Y
,
F
Y
(
1
F
Y
)
{\displaystyle \eta _{Y}=\Phi _{Y,FY}(1_{FY})}
1
F
Y
=
ε Δ -->
F
Y
∘ â -->
F
(
η η -->
Y
)
{\displaystyle 1_{FY}=\varepsilon _{FY}\circ F(\eta _{Y})}
ăćŸăăäžçȘçźăźć
ŹćŒăźY ă«GX ă代ć
„ăăf ă«
ε Δ -->
X
=
Φ ÎŠ -->
G
X
,
X
− â -->
1
(
1
G
X
)
{\displaystyle \varepsilon _{X}=\Phi _{GX,X}^{-1}(1_{GX})}
1
G
X
=
G
(
ε Δ -->
Y
)
∘ â -->
η η -->
G
X
{\displaystyle 1_{GX}=G(\varepsilon _{Y})\circ \eta _{GX}}
ăćŸă
é䌎éąæăźèăăŻăăăšă«ă»ă«ăł ă«ăăŁăŠ1958ćčŽă«ćźćŒćăăăăć€ăăźćè«ăźæŠćż”ăšćæ§ă«ăăăąăăžăŒä»Łæ° ă«ăăăŠèšçźăèĄăăăšăăéă«ćż
èŠă«ăȘăŁăăăă«ć°ć
„ăăăăăăźćéĄăźăăăă§çł»ç”±çăȘèĄšçŸăäžăăăăšćăćăŁăäșșă
ăŻăąăŒăă«çŸ€ ăźćă«ăăăŠ
hom(F (X ), Y ) = hom(X , G (Y )) ăźăăăȘéąäżăăăăăšă«æ°ă„ăăŠăăăăăă§ăF ăŻéąæ
− â -->
⊗ â -->
A
{\displaystyle -\otimes A}
A ăšăăłăœă«ç© ăćă)ă§ăăăG ăŻéąæhom(A ,â)ă§ăăăăăă§çć· ăäœżăăźăŻèšć·ăźäč±çš ă§ăăăăăăăźçŸ€ăŻćźéă«ăŻçăăăȘăăăçăăèŠăăăăăȘèȘç¶ăȘ æčæłăăăăèȘç¶ă«æăăăăçç±ăšăăŠăäžçȘă«ăć
ă
ăŻăăăăX Ă A ăăY ăžăźćç·ćœąćć ăź2ă€ăźç°ăȘăŁăèĄšçŸă§ăăăăă§ăăăăăăăăăăŻăăłăœă«ç©ă«éąăăăăă¶ăćșæăȘ話ă§ăăăćè«ă«ăăăŠăźć
šćć°ăźèȘç¶æ§ăŻèȘç¶ććăźæŠćż”ăć
ă«ăȘăŁăŠăăă
ăăźçšèȘăŻăă«ăă«ăç©șé ă«ăăăŠăäžèšăźhoméćăźéăźéąäżăšäŒŒăéąäż
⟨ âš -->
T
x
,
y
⟩ â© -->
=
⟨ âš -->
x
,
U
y
⟩ â© -->
{\displaystyle \langle Tx,y\rangle =\langle x,Uy\rangle }
é䌎äœçšçŽ T ăšU ăăæ„ăŠăăăF ăŻG ăźć·Šé䌎 ăšăăăG ăŻF ăźćłé䌎 ăšăăăăă ăăG èȘèș«ăF ăšăŻăăȘăç°ăȘăŁăćłé䌎ăæăĄăă(仄äžăźäŸăèŠă)ăăăçšźăźæèă«ăăăŠăŻăè©łçŽ°ăȘăă«ăă«ăç©șéăźé䌎ććăźăąăăăžăŒăćŻèœă§ăă[ 1]
ăăăăźé䌎éąæăźćŻŸăæąăć§ăăăšăćźăŻæœè±Ąä»Łæ° ă§ăŻéćžžă«ăăă”ăăăăšă§ăăăä»ăźćéă§ăćæ§ă§ăăăăšăćăăă仄äžăźäŸăźçŻă§ăŻăăźèšŒæ ăäžăăăăăă«ăæźéçæ§æăŻăăŁăšæźéă«ăăăăăźé䌎éąæăźćŻŸă«æăĄäžăăăăšăă§ăăă
æ°ćŠè
ăŻäžèŹçă«ăŻćźć
šăȘé䌎éąæăźæŠćż”ăćż
èŠăšăăŠăăăăă§ăŻăȘăăćœŒăăźè§ŁăăăšăăŠăăćéĄă«ăăŁăŠăăăă蚌æă«ćż
èŠăă©ăăă§ćż
èŠăȘæŠćż”ăă©ăăăć€ćźăăŠăăăćè«ăźćææź”éă§ăă1950ćčŽä»Łă«ăŻăăăăźćæ©ă«ć€§ăăćŒăŁćŒ”ăăăŠăăăăąăŹăŻă”ăłăă«ă»ă°ăăżăłăăŁăŒăŻ ăźæ代ă«ăȘăŁăŠăćè«ăŻä»ăźä»äșă«ăăăæéăšăăŠäœżăăăăăă«ăȘăŁăăăŻăăăŻéąæ°è§Łæ ăšăăąăăžăŒä»Łæ° ă§ăăæç”çă«ăŻä»Łæ°ćčŸäœ ă§äœżçšăăăă
ćœŒăé䌎éąæăźæŠćż”ăćéąăăăšăăăźăŻăăăăèȘ€ăŁăŠăăăšăăăăăé䌎ăźçčć„ăȘćœčćČă«ă€ăăŠă°ăăżăłăăŁăŒăŻćșæăźèȘèăŻăăŁăăäŸăă°ăćœŒăźèćăȘæ„瞟ăźăČăšă€ă«ăçžćŻŸćăźă»ăŒă«ććŻŸæ§ ăăă ăăŠăăăšă代æ°ć€æ§äœăźéŁç¶ăȘæă«éąăăă»ăŒă«ććŻŸæ§ăăăăăăźèšŒæăźć
šäœăŻç”ć±ăźăšăăăăéąæăźćłé䌎ăććšăăăăšăăăăšă«ăȘăăăăăŻćźć
šă«æœè±Ąçă§éæ§æçă§ăăăăăăăȘăă«ćŒ·ćă§ăăăă
ăăčăŠăźćé ćșéć ăŻćăšăżăȘăăăšăă§ăă(x †y ă§ăăăšăă«ăăŸăăăźăšăăźăżă x ăšy ăźéă«ăŻ1ă€ă ăć°ăăăăšăă)ă2ă€ăźćé ćșéćăźéăźé䌎éąæćŻŸăŻăŹăăąæ„ç¶ ăšćŒă°ăă(ăăăŠăćć€ăźć ŽćăŻăantitone ăŹăăąæ„ç¶ă§ăă)ăăŹăăąæ„ç¶ăźèšäșă«ć€ăăźäŸăăăăăšăă«ăŹăăąçè« ăäžçȘăźäŸă§ăăăä»»æăźăŹăăąæ„ç¶ăŻéć
äœçšçŽ ăćŻŸćżăăéăăèŠçŽ éăźéé ćșăäżćăăć
šćć°ă«æăĄäžăăăăšăćșæ„ăă
ăŹăăąçŸ€ăźć Žćăšćæ§ă«ăćźéăźèćłăŻăă°ăă°ććŻŸăšăźćŻŸćż(äŸăă°ăantitone é ćșăźćć)ăè©łçŽ°ćăăŠăăăăšă«ăăăKaplansky ăăăăźăŹăăąçè«ăźæăăæčăŻăăăă«äžèŹçăȘæ§é ăăăăăšăžăźèȘèă«ćœ±éżăäžăăă
ćé ćșăźć Žćăźé䌎ăźćźçŸ©ăŻèăăă€ă¶ăăŠăăăăăăă€ăăźăăŒăăäžăăŠăăăă
é䌎ăŻććŻŸăććă§ăȘăăŠăăăăăăăăă«ææ ŒăăéăźćèŁăšăăăăšăćșæ„ă
éć
äœçšçŽ ăŻćŻŸćżăăăąăăă«ăăé䌎ăźććšăç€șăăăšăăă(Kuratowski closure axioms ăćç
§)
William Lawvere ă«ăăéćžžă«äžèŹçăȘè§ŁèȘŹ[ 2] C ăć
šăŠăźè«ç(ć
Źçć)ăăăȘăéćăšăăD ăć
šăŠăźæ°ćŠçæ§é ăăăȘăéćăźćȘéćăšăăăC ăźćçè«T ă«ćŻŸăăŠăF (T )ăć
ŹçT ăæșăăæ§é ć
šăŠăăăȘăéćăšăăćæ°ćŠçæ§é ăźæS ă«ćŻŸăăŠăG (S )ăŻS ăźæć°ăźć
ŹçćăšăăăăăźăšăăF (T )ăS ăźéšćéćă§ăăăăšăšăG (S )ăT ăźè«ççćž°ç”ă§ăăăăšăŻćć€ă§ăăăăæćłéąæăF ăŻăæ§æéąæăG ăźć·Šé䌎ă§ăăăäčçźăźéăšăăŠăź(äžèŹăź)æŒçźăšăăŠăźé€çźăŻăć€ăăźäŸăăăăäŸăă°ăèż°èȘè«çă«ăăăć«æăźć°ć
„èŠćăăç°ăźă€ăăąă« ă«ăăă€ăăąă«ć ăŻăé䌎ăäžăăăăźăšèŠăăăšăă§ăăă ăăźăăăȘèŠłćŻăŻć
šăŠăźæ°ćŠă§äŸĄć€ăźăăăăźă§ăăă
èȘç±çŸ€ ăźæ§æăŻæ„”ăăŠæźéăźé䌎ă«ăăæ§æă§ăăăäžèšăźè©łçŽ°ăźćăăăăăăŠäŸżć©ăȘäŸă§ăăă
éąæF : Grp Set Y ă«Y ăźèŠçŽ ăźçæăăèȘç±çŸ€ăćŻŸćżăăăăăźăšăăéąæG : Grp â Set ăŻçŸ€X ă«ăăźć°éćăćŻŸćżăăăćżćŽéąæ ăšăăă仄äžă«ç€șăăăă«F ăŻG ăźć·Šé䌎ăšăȘăă
ăç”ăæźéć° ăć矀X ă«ă€ăăŠă矀FGX ăŻGX ăźçæăăăăăȘăăĄX ăźć
ăăĄăçæăăèȘç±çŸ€ă§ăăă矀ăźæșćć
ε Δ -->
X
:
F
G
X
→ â -->
X
{\displaystyle \varepsilon _{X}:FGX\to X}
FGX ăźçæć
ăćŻŸćżăăX ăźć
ă«ćăăăźăšăăăăăăŻèȘç±çŸ€ăźæźéæ§ăăćžžă«ććšăăăăăźăšă
(
G
X
,
ε Δ -->
X
)
{\displaystyle (GX,\varepsilon _{X})}
F ăăX ăžăźæźéć°ă§ăăăăȘăăȘăăèȘç±çŸ€FZ ăăX ăžăźçŸ€ăźæșććăŻ
ε Δ -->
X
:
F
G
X
→ â -->
X
{\displaystyle \varepsilon _{X}:FGX\to X}
Z ăăGX ăžăźććç”ç±ă§ćè§Łăăăăăă§ăăăăăăŻ(F , G )ăé䌎ăźćŻŸă§ăăăăšăæćłăăă
ăć§ăæźéć° ăćéćY ă«ćŻŸăăŠăGFY ăŻćă«Y ăźçæăăèȘç±çŸ€FY ăźć°éćă§ăăăćć
η η -->
Y
:
Y
→ â -->
G
F
Y
{\displaystyle \eta _{Y}:Y\to GFY}
(
F
Y
,
η η -->
Y
)
{\displaystyle (FY,\eta _{Y})}
Y ăăG ăžăźæźéć°ă§ăăăăȘăăȘăăY ăăGW ăźć°éćăžăźććăŻ
η η -->
Y
:
Y
→ â -->
G
F
Y
{\displaystyle \eta _{Y}:Y\to GFY}
FY ăăW ăžăźäžæçăȘ矀ăźæșććç”ç±ă§ćè§Łăăăăăă§ăăăăăă(F , G )ăé䌎ăźćŻŸă§ăăăăšăæćłăăă
homéćé䌎 ăèȘç±çŸ€FY ăă矀X ăžăźçŸ€æșććăŻæŁçąșă«éćY ăăéćGX ăžăźććă«ćŻŸćżăăăăăȘăăĄăFY ăăX ăžăźć°ăŻçæć
ăžăźäœçšă«ăăćźć
šă«æ±șćźăăăăăăźćŻŸćżăèȘç¶ććă§ăăăăšăçŽæ„çąșèȘă§ăăăăăŁăŠ(F ,G )ă«ćŻŸćżăăhoméćăźé䌎ăćŸăăăă
äœćäœ-ćäœé䌎 ăΔăšÎ·ăèȘç¶ă§ăăăăšăŻçŽæ„çąșăăăăăăăăăŠăäœćäœ-ćäœé䌎
(
ε Δ -->
,
η η -->
)
:
F
⊣ ⣠-->
G
{\displaystyle (\varepsilon ,\eta ):F\dashv G}
1ă€çźăźäœćäœ-ćäœæçćŒ
1
F
=
ε Δ -->
F
∘ â -->
F
η η -->
{\displaystyle 1_{F}=\varepsilon F\circ F\eta }
Y ă«ćŻŸăăŠăćæ
F
Y
→
F
(
η η -->
Y
)
F
G
F
Y
→
ε Δ -->
F
Y
F
Y
{\displaystyle FY{\xrightarrow {\;F(\eta _{Y})\;}}FGFY{\xrightarrow {\;\varepsilon _{FY}\,}}FY}
ăæçć°ă§ăăăšăăăăšă§ăăăéäžăźçŸ€FGFY ăŻèȘç±çŸ€FY ăźèȘăăĄăăçæăăăèȘç±çŸ€ă§ăăă(仄éăæŹćŒ§ă§ăăăăăèȘăŻçŹç«ăăçæć
ăèĄšăăăšă«ăă)ăć°
F
(
η η -->
Y
)
{\displaystyle F(\eta _{Y})}
FY ăăFGFY ăžăźçŸ€ăźćć°æșććă§ăăăFY ăźçæć
y ăćŻŸćżăăFGFY ăźçæć
ă§ăăé·ă1ăźèȘ (y ) ă«ćăăć°
ε Δ -->
F
Y
{\displaystyle \varepsilon _{FY}}
FGFY ăăFY ăžăźçŸ€ăźæșććă§ăăăçæć
ăćŻŸćżăăFY ăźèȘă«ćă(ă€ăŸăăæŹćŒ§ăć€ăă)ăăăăăźćæăŻăăĄăăFY ăźæçć°ă§ăăă
2ă€çźăźäœćäœ-ćäœæçćŒ
1
G
=
G
ε Δ -->
∘ â -->
η η -->
G
{\displaystyle 1_{G}=G\varepsilon \circ \eta G}
X ă«ćŻŸăăŠăćæ
G
X
→
η η -->
G
X
G
F
G
X
→
G
(
ε Δ -->
X
)
G
X
{\displaystyle GX{\xrightarrow {\;\eta _{GX}\;}}GFGX{\xrightarrow {\;G(\varepsilon _{X})\,}}GX}
ăæçć°ă§ăăăšăăăăšă§ăăăéäžăźéćGFGX ăŻćă«FGX ăźć°éćă§ăăăć°
η η -->
G
X
{\displaystyle \eta _{GX}}
GX ăăéćGFGX ăžăźăçæć
ăăĄăźć
ć«ăććă§ăăăć°
G
(
ε Δ -->
X
)
{\displaystyle G(\varepsilon _{X})}
GFGX ăăéćGX ăžăźććă§ăFGX ăźçæć
ăX ăźć
ă«ćă(ăæŹćŒ§ăć€ăă)ăšăă矀ăźæșććăźć°ă§ăăăăăăăźćæăŻăăĄăăGX ăźæçć°ă§ăăă
èȘç±ćŻŸè±Ą ăŻć
šăŠćżćŽéąæ ăźć·Šé䌎ăźäŸăšăȘăăăăă§ćżćŽéąæăŻä»Łæ°çćŻŸè±Ąăăăźć°éćă«ćăăăăăăźä»Łæ°çăȘèȘç±éąæ ă«ćŻŸăăŠăăäžèšăźèȘç±çŸ€ă«è©łçŽ°ă«èšèż°ăăăăźăšćæ§ăźăăšăäžèŹă«æăç«ă€ă
ç© ăćŒăæ»ă ăçćć ăæ ž ăŻă©ăăćè«çăȘæ„”éăźäŸă§ăăăć
šăŠăźæ„”ééąæăŻćŻŸćżăăćŻŸè§éąæ(èăăŠăăæ„”éăźçšźéĄăăæ±șăŸă)ăźćłé䌎ă§ăăăé䌎ăźäœćäœăŻæ„”éćŻŸè±Ąăăăź(ă€ăŸăăéąæćă«ăăăăèăăŠăăæ„”éă«ćŻŸćżăăćŻŸè§éąæăăăź)ćźçŸ©ć°ăäžăăă仄äžă«ćă
ăźäŸăç€șăă
ç© éąæÎ : Grp2 â Grp ăććŻŸ(X 1 , X2 )ă«çŽç©çŸ€X 1 ĂX 2 ăćŻŸćżăăăăăźăšăăéąæÎ : Grp2 â Grp ăć矀X ă«ç©ćGrp2 ăźćŻŸè±Ą(X , X )ăćŻŸćżăăăćŻŸćŻŸè§éąæăšăăăçŽç©çŸ€ăźæźéæ§ăăÎ ăŻÎăźćłé䌎ă§ăăăăšăćăăăăăźé䌎ăźcounităŻæ„”éăćźăăX 1 ĂX 2 ăăX 1 ăš X 2 ăžăź2ă€ăźć°ćœ±ăźćŻŸă§ăăć°ă§ăăăunităŻçŸ€X ăăX 1 ĂX 2 ăźäžăžăźćŻŸè§ć
ć«ć° (x ă(x , x )ă«ćă)ă§ăăăéćăźăă«ă«ăç© ăç°ăźçŽç©ăäœçžç©șéăźçŽç©ăȘă©ăćăă§ăăăăăă«2ă€ä»„äžăźć ŽćăçŽ çŽăȘæčæłă§æĄćŒ”ă§ăăăăăŁăšäžèŹă«ăŻăă©ăźçšźéĄăźæ„”éăćŻŸè§éąæăźćłé䌎ă§ăăă æ ž ăąăŒăă«çŸ€ăźæșććăźćD ăèăăăD ăź2ă€ăźćŻŸè±Ąf 1 : A 1 â B 1 ăšf 2 : A 2 â B 2 ă«ćŻŸăăŠăf 1 ăă f 2 ăžăźć°ăŻăćŻŸ(g A g B gB f 1 = f 2 gA ăæșăăăăźăźăăšăăăăéąæG : D â Ab ăćæșććăăăźæ žă«ćŻŸćżăăăăăźăšăăéąæF : D â Ab ăć矀A ă矀æșććA â 0ă«ćŻŸćżăăăăăźăšăăăG ăŻF ăźćłé䌎ă§ăăăăăăŻæ žăźæźéæ§ăç€șăăŠăăăăăźé䌎ăźäœćäœć°ăŻæșććăźæ žăăăźć§ćă«ćă蟌ăć°ă§ăăăćäœć°ăŻçŸ€A ăæșććA â 0ăźæ žăšćäžèŠăăć°ă§ăăăăăźäŸăźé©ćăȘć€çšźăšăăŠăç·ćœąç©șéăć 矀ăźæ žéąæăćłé䌎ă§ăăăćæ§ă«ăăąăŒăă«çŸ€ăç·ćœąç©șéăć 矀ăźäœæ žéąæăć·Šé䌎ă§ăăăăšăćăăă
äœç© ăæŒăćșă ăäœçćć ăäœæ ž ăŻăăăăćè«ă«ăăăäœæ„”éăźäŸăă§ăăă
ć
šăŠăźäœæ„”ééąæăŻćŻŸćżăăćŻŸè§éąæ(èăăŠăăäœæ„”éăźçšźéĄăăæ±șăŸă)ăźć·Šé䌎ă§ăăăé䌎ăźunităŻäœæ„”éćŻŸè±ĄăžăźćźçŸ©ć°ăäžăăă仄äžă«ćă
ăźäŸăç€șăă
äœç© éąæF : Ab Ab2 ăćăąăŒăă«çŸ€ăźćŻŸ(X 1 , X 2 )ă«çŽćăćŻŸćżăăăăăźăšăăéąæG : Ab â Ab2 ăćăąăŒăă«çŸ€Y ă«ćŻŸ(Y , Y )ăćŻŸćżăăăăăźăšăăăăăźăšăF ăŻG ăźć·Šé䌎ă§ăăăăăĄăăçŽćăźæźéæ§ăăć°ăăăăăăźé䌎ăźunităŻX 1 ăš X 2 ăăçŽćăžăźć
ć«ććăźćŻŸăăăȘăć°ă§ăăăcounităŻ(X ,X )ăźçŽćăăX ăžăźć çźă«ăăć°ă§ăă(çŽćăźć
(a , b )ă«X ăźć
a +b ăćŻŸćżăăă)ćæ§ăźäŸăšăăŠć 矀ăç·ćœąç©șéăźçŽćăă矀ăźèȘç±ç©ăéćăźéäș€ćăăăă
éćäœçç°ăžăźćäœć
æ·»ć ăăăăŻćæ©ăźçŻă§è°è«ăăäŸă§ăăăéćäœçç° R ăäžăăăăăšăăŠăR ĂZ ăéžăłăZ ćç·ćœąăȘç©ă(r,0)(0,1) = (0,1)(r,0) = (r,0)ă (r,0)(s,0) = (rs,0)ă (0,1)(0,1) = (0,1)ă§ćźăăăăšă«ăăăäčæłćäœć
ăèżœć ăăăăšăćșæ„ăăăăźæ§æăŻç°ăźć°ăšăȘăéćäœçç°ăćăéąæăźć·Šé䌎ă§ăăăç°ăźæĄć€§ ăR ăšS ăç°ăšăăÏ : R â S ăç°ăźæșććăšăăăăăźăšăS ăŻăć·ŠăR -ć 矀ăšăżăȘăăăšăă§ăăS ăšăźăăłăœă«ç© ăŻéąæF : R -Mod â S -Mod ăćŒăè”·ăăăăăăŠăF ăŻćżćŽéąæG : S -Mod â R -Mod ăźć·Šé䌎ă§ăăăăăłăœă«ç©æ§æ ăR ăç°ăM ăćłR -ć 矀ăšăăM ăšăźăăłăœă«ç©ăŻéąæF : R -Mod â Ab ăćŒăè”·ăăăéąæG : Ab â R -Mod ăăćăąăŒăă«çŸ€A ă«ćŻŸăăŠăG (A ) = homZ M ,A )ă§ćźăăăšăF ăźćłé䌎ăšăȘăă矀ç°æ§æ ăæŽäżæ°ăąăă€ăç° æ§æăŻăąăă€ă ăăç°ăžăźéąæăäžăăăăăźéąæăŻćç°ăăăźć°ăšăȘăäčæłăąăă€ăă«ćăéąæăźć·Šé䌎ă§ăăăćæ§ă«æŽäżæ°çŸ€ç° æ§æăŻçŸ€ăăç°ăžăźéąæăäžăăćç°ăăăźćć
矀 ă«ćăéąæăźć·Šé䌎ă§ăăăïŒæŽäżæ°ă§ăŻăȘăïŒäżæ°äœ K ăäžăăć Žćăç°ăźćăźăăăă« K -代æ°ăźćăäœżăă° K äžăźăąăă€ăç°ă矀ç°ăćŸăăăăćäœæ§æ ăæŽćăźćă§ć°ăćć°ă«éăŁăăăźăDom m ăšæžăăăšă«ăăăćżćŽéąæField â Dom m ăŻć·Šé䌎ăæă€ăăăăŻć
šăŠăźæŽćă«ćăźäœ ăćČăćœăŠăăć€é
ćŒç° ăRing * ăćșçčä»ăćŻæç°ăźćăšăă(ç°A ăšăăźć
a ăźćŻŸ (A , a )ăćŻŸè±ĄăšăăŠăć°ăŻăăźćșć„ăăăć
ăäżćăăæșććăšăă)ăćżćŽéąæG:Ring * â Ring ăŻć·Šé䌎ăæăĄăćç°R ă«ćŻŸăăŠ(R [x ], x )ăćČăćœăŠăăăăă§R [x ]ăŻR ăäżæ°ăšăăć€é
ćŒç° ă§ăăăăąăŒăă«ć : ăąăŒăă«çŸ€ăă矀ăžăźć
ć«éąæG : Ab â Grp ăèăăăšăăąăŒăă«ć ăšćŒă°ăăć·Šé䌎ăæă€ăăăăŻć矀G ă«ć矀G ab =G /[G ,G ]ăćČăćœăŠăăă°ăăżăłăăŁăŒăŻæ§æ : çșç«ŻăŻăK-çè« ă«ăăăŠäœçžç©șé äžăźăăŻăă«æ ăźćăçŽć ăźäžă§ćŻæăąăă€ăæ§é ăæă€ăăšă§ăăăćăăŻăă«æïŒăźćć€éĄïŒă«ć æłéć
ăćœąćŒçă«èżœć ăăăăšă«ăăăăăźăąăă€ăăă°ăăżăłăăŁăŒăŻçŸ€ ăšćŒă°ăăăąăŒăă«çŸ€ ă«ăăăăšăă§ăăăćăăăšă ăăć矀ăïŒéć
ăźććšăćżăăăăšă«ăăïŒăăźć°ăšăȘăăąăă€ăăžćăćœæăŻć·Šé䌎ăæă€ăăăźăăăȘă°ăăżăłăăŁăŒăŻæ§æăŻăèȘç¶æ°ăăăźèČ ăźæŽæ°ăźæ§æăăȘăăăăă«ăăăăšăă§ăăăăććšćźç ăšăăŠäœżăăăšăăăăæéé
æŒçźăźä»Łæ°æ§é ăźć Žćă«ćŻŸăăŠăŻăăăźăăăȘæ§æăźććšæ§ăŻæźé代æ°ćŠ ăăąăă«çè« ă«èšćăăăăšăă§ăăăăćè«çă«é©ćœăȘćœąă§ăźèšŒæăšăăŠăèȘç¶ă«èż°ăčăăăă矀ăźèĄšçŸè«ă«ăăăăăăăăŠăčçžäșćŸ ă«ăăă°ăèĄšçŸăźèȘć° ăŻèĄšçŸăźć¶éăźć·Šé䌎ă§ăăă
ć·Šé䌎ăšćłé䌎ăæă€éąæ ăG ăäœçžç©șé ăăéćăžăźéąæă§ăćäœçžç©șéă«ăăźć°éćăćČăćœăŠăăăźăšăă (äœçžăćżăă)ăG ăŻć·Šé䌎 F ăæăĄăéć Y äžă«éąæŁäœçž ăćźăăăG ăŻćłé䌎 H ăæăĄăY ă«ćŻçäœçž ăćźăăăæžćăšă«ăŒăç©șé ăäœçžç©șéX ăšY ă«ćŻŸăăŠăX ăźæžć SX ăăY ăžăźéŁç¶ććăźăăąăăăŒéĄ ăăȘăç©șé [SX , Y ] ăŻX ăăY ăźă«ăŒăç©șé ΩY ăžăźéŁç¶ććăźăăąăăăŒéĄăăȘăç©șéăšèȘç¶ććă§ăăăăăăŻăăąăăăŒè« ă§éèŠă§ăăăăčăăŒăł–ăă§ăăŻăłăłăăŻăć ăKHaus ăăłăłăăŻă [èŠææ§ăćéż ăăŠăčăă«ă ç©șéăźćăšăăG : KHaus â Top ăäœçžç©șéăźćăžăźć
ć«éąæăšăăăăăźăšăăG ăŻć·Šé䌎F : Top â KHaus ăæăĄăăčăăŒăłâăă§ăăŻăłăłăăŻăć ăšăȘăăăăźé䌎ăźcounităŻćäœçžç©șéX ăăăăźăčăăŒăłâăă§ăăŻăłăłăăŻăćăźäžăžăźéŁç¶ććă§ăăăX ăăăłăăç©șé ă§ăăăšăăăŸăăăźăšăăźăżăăăźććăŻćăèŸŒăż (ă€ăŸăăćć°ăȘéŁç¶éćć)ă§ăăăć±€ăźé ćăšéć ăć
šăŠăźéŁç¶ććf : X â Y ăŻX äžăźć±€ (éćăźć±€ăăąăŒăă«çŸ€ăźć±€ăç°ăźć±€ăȘă©)ăăY ăźćŻŸćżăăć±€ăžăźéąæf â ăèȘć°ăăé ćéąæ Y äžăźăąăŒăă«çŸ€ăźć±€ăăX äžăźăąăŒăă«çŸ€ăźć±€ăžăźéąæ f â1 ăèȘć°ăăăéćéąæ f â1 㯠f â ăźć·Šé䌎ă§ăăăăăă§ćŸźćŠăȘçčăŻéŁæ„ć±€ ă§ăźć·Šé䌎ăŻ(éćăź)ć±€ăźăăăšăŻç°ăȘăŁăŠăăăăšă§ăăăsoberć ăăčăăŒăłććŻŸæ§ ăźèšäșă«ăăăăă«ăäœçžç©șéăźćăšsoberç©șé ăźćăŻé䌎ă§ăăăçčă«ăăăźèšäșăŻpointless topology ă§èŠă€ăăŁăăsoberç©șéăšspatial localeăźéăźæćăȘććŻŸæ§ăźăăăźć„ăźé䌎ăè©łçŽ°ă«èšèż°ăăŠăăă
é䌎ăźć ăéąæÏ0 ăććă«ăăźéŁç”æćăäžăăéąæăšăăăšăăăăŻćéćă«éąæŁćăćČăćœăŠăéąæD ăźć·Šé䌎ă§ăăăăăă«ăD ăŻćă«ćŻŸè±ĄéćăćČăćœăŠăćŻŸè±ĄéąæU ăźć·Šé䌎ă§ăăăæćŸă«ăU ăŻćéćă«indiscretećăćČăćœăŠăéąæăźć·Šé䌎ă§ăăăææ°ćŻŸè±Ą ăă«ă«ăéć ă«ăăăŠâĂA ă§ćźăŸăèȘć·±éąæC â C ăŻćłé䌎âA
Categorical logic
ăăźçŻăź
ć ç ăæăŸăăŠăăŸăă
ïŒ2009ćčŽ11æ ïŒ
quantification Any morphism f : X â Y in a category with pullbacks induces a monotonous map
f
∗ â -->
:
Sub
(
Y
)
→ â -->
Sub
(
X
)
{\displaystyle f^{*}:{\text{Sub}}(Y)\to {\text{Sub}}(X)}
∃ â -->
f
{\displaystyle \exists _{f}}
∀ â -->
f
{\displaystyle \forall _{f}}
[ 3] In the category of sets, if we choose subsets as the canonical subobjects, then these functions are given by:
(
T
⊆ â -->
Y
)
↦ ⊠-->
f
∗ â -->
(
T
)
=
f
− â -->
1
[
T
]
{\displaystyle (T\subseteq Y)\;\mapsto \;f^{*}(T)=f^{-1}\lbrack T\rbrack }
(
S
⊆ â -->
X
)
↦ ⊠-->
∃ â -->
f
S
=
{
y
∈ â -->
Y
∣ ⣠-->
∃ â -->
x
∈ â -->
f
− â -->
1
[
{
y
}
]
,
x
∈ â -->
S
}
=
f
[
S
]
{\displaystyle (S\subseteq X)\;\mapsto \;\exists _{f}S=\{\;y\in Y\;\mid \;\exists x\in f^{-1}\lbrack \{y\}\rbrack ,x\in S\;\}=f\lbrack S\rbrack }
(
S
⊆ â -->
X
)
↦ ⊠-->
∀ â -->
f
S
=
{
y
∈ â -->
Y
∣ ⣠-->
∀ â -->
x
∈ â -->
f
− â -->
1
[
{
y
}
]
,
x
∈ â -->
S
}
{\displaystyle (S\subseteq X)\;\mapsto \;\forall _{f}S=\{\;y\in Y\;\mid \;\forall x\in f^{-1}\lbrack \{y\}\rbrack ,x\in S\;\}}
See also powerset for a slightly simplified presentation.
ć
šăŠăźéąæ G : đ â đđ ăćźćć ă§ăăăšăăŻăć·Šé䌎ăæă€éąæăŻPeter J. Freyd ăźé䌎éąæćźç ăG ăć·Šé䌎ăæă€ăăăźćż
èŠććæĄä»¶ăŻăăăăéŁç¶(æ„”éăäżă€)ăă€ăăăçšźăźăéćæ§(ć°ăă)ăæĄä»¶ăăżăăăăšă§ăăăă§çčćŸŽä»ăăăăăć
·äœçă«ăŻăđ ăźććŻŸè±Ą Y ă«ćŻŸăăŠăéć (ă€ăŸăçăŻă©ăč ă§ăȘăéćăšăăæćłă§ăć°ăăă) I ăźć
ă§æ·»ćä»ăăăăć°ăźæ f i Y â G (Xi )h : Y â G (X )i ∈ I t : X i X ∈ C h = G (t ) â f i
ćæ§ăźăăšăćłé䌎ă«éąăăŠăæăç«ă€ă
éąæF : C â D ă2ă€ăźćłé䌎G ăšGâČ ăæă€ăšăăăšăG ăšGâČ ăŻèȘç¶ććă§ăăăć·Šé䌎ă«ă€ăăŠăćæ§ă§ăăă
éă«ăF ăG ăźć·Šé䌎ă§ăăăG ăšGâČ ăèȘç¶ććă§ăăăšăăăšăF ăŻGâČ ăźć·Šé䌎ă§ăăăăăăäžèŹă«ăŻăăF , G , Δ, ηăă(Δ,η)ăcounit-unităšăăé䌎ă§ăăă
Ï : F â F âČ
Ï : G â G âČ ăăšăă«èȘç¶ććă§ăăăšăăăšăăF âČ, G âČ, ΔâČ, ηâČăăé䌎ă§ăăăăăă§ă
η η -->
′
=
(
τ Ï -->
∗ â -->
σ Ï -->
)
∘ â -->
η η -->
ε Δ -->
′
=
ε Δ -->
∘ â -->
(
σ Ï -->
− â -->
1
∗ â -->
τ Ï -->
− â -->
1
)
.
{\displaystyle {\begin{aligned}\eta '&=(\tau \ast \sigma )\circ \eta \\\varepsilon '&=\varepsilon \circ (\sigma ^{-1}\ast \tau ^{-1}).\end{aligned}}}
ă§ăăă
∘ â -->
{\displaystyle \circ }
∗ â -->
{\displaystyle \ast }
é䌎ăŻèȘç¶ăȘăăæčă§ćæă§ăăăæç€șçă«æžăăšăC ăšD ăšăźéăźé䌎ăF , G , Δ, ηăăšD ăšE ăšăźéăźé䌎ăF âČ, G âČ, ΔâČ, ηâČăăäžăăăăăšăăéąæ
F
′
∘ â -->
F
:
C
← â -->
E
{\displaystyle F'\circ F:{\mathcal {C}}\leftarrow {\mathcal {E}}}
ăŻéąæ
G
∘ â -->
G
′
:
C
→ â -->
E
.
{\displaystyle G\circ G':{\mathcal {C}}\to {\mathcal {E}}.}
ăźć·Šé䌎ă§ăăăăăă«è©łăăæžăăšăF âČ F ăšG G âČăźéăźé䌎ăźunităšcounităŻä»„äžăźćæă§äžăăăăă
1
E
→
η η -->
G
F
→
G
η η -->
′
F
G
G
′
F
′
F
F
′
F
G
G
′
→
F
′
ε Δ -->
G
′
F
′
G
′
→
ε Δ -->
′
1
C
.
{\displaystyle {\begin{aligned}&1_{\mathcal {E}}{\xrightarrow {\eta }}GF{\xrightarrow {G\eta 'F}}GG'F'F\\&F'FGG'{\xrightarrow {F'\varepsilon G'}}F'G'{\xrightarrow {\varepsilon '}}1_{\mathcal {C}}.\end{aligned}}}
ăăźæ°ăăé䌎ăŻäžăăăă2ă€ăźé䌎ăźćæăšćŒă°ăăă
ăăă«ăăăć°ăăȘć ăćŻŸè±Ąăšăăé䌎ăć°ăšăăćăäœăăăšăćșæ„ăă
é䌎ăźăăŁăšăéèŠăȘæ§èłȘăŻéŁç¶æ§ă§ăăăć·Šé䌎ăæă€ć
šăŠăźéąæ(ă€ăŸăćłé䌎ă§ăă éąæ)ăŻéŁç¶ ă§ăă(ă€ăŸăćè«ă§ăźæ„”éăšćŻæă§ăă)ăćłé䌎ăæă€ć
šăŠăźéąæ(ă€ăŸăć·Šé䌎ă§ăă éąæ)ăŻäœéŁç¶ ă§ăă(ă€ăŸăäœæ„”éăšćŻæă§ăă)ă
æ°ćŠă«ăăăć€ăăźć
±éăźæ§æăŻæ„”éăäœæ„”éă§ăăăźă§ăăăźăăšăŻăăăăăźæ
ć ±ăăăăăăäŸăă°ă
ćŻŸè±Ąăźç©ă«ćłé䌎éąæăé©çšăăç”æăŻćăźç©ă§ăă
ćŻŸè±Ąăźäœç©ă«ć·Šé䌎éąæăé©çšăăç”æăŻćăźäœç©ă§ăă
ć
šăŠăźćłé䌎éąæăŻć·Šćźć
š ă§ăă
ć
šăŠăźć·Šé䌎éąæăŻćłćźć
š ă§ăă
C ăšD ăćć æłć ăšăăF : C â D ăć æłçéąæ ăšăăG : C â D ăF ăźćłé䌎ă§ăăăšăăăšăG ăć æłçéąæă§ăăăhoméćăźć
šćć°
Φ ÎŠ -->
Y
,
X
:
h
o
m
C
(
F
Y
,
X
)
≅ â
-->
h
o
m
D
(
Y
,
G
X
)
{\displaystyle \Phi _{Y,X}:\mathrm {hom} _{\mathcal {C}}(FY,X)\cong \mathrm {hom} _{\mathcal {D}}(Y,GX)}
ăŻăćźăŻăăąăŒăă«çŸ€ăźććă§ăăăććŻŸçă«ăG ăć æłçă§ăF ăG ăźć·Šé䌎ă§ăăăšăăăšăF ăăŸăć æłçă§ăăă
ăăă«ăC ăšD ăć æłć (ă€ăŸăăćć æłćă§ăăæéćç© ăăă€)ăšăăăšăä»»æăźé䌎éąæăźćŻŸăŻèȘćçă«ć æłçăšăȘăă
ćăă«æžăăăăă«ăćC ăšD ăźé䌎ăŻ2ă€ăźæźéć°ăźæă«æăĄäžăăăăšăă§ăăăçæčăŻC ăźćŻŸè±Ąă«ă€ăăŠăăăçæčăŻD ăźćŻŸè±Ąă«ă€ăăŠăźæźéć°ă§ăăăéă«ăD ăźććŻŸè±ĄăăéąæG : C â D ăžăźæźéć°ăććšăăăšăăG ăŻć·Šé䌎ă§ăăă
ăăăăæźéçæ§æăŻé䌎éąæăăăăŁăšäžèŹçă§ăăăæźéçæ§æăŻæé©ććéĄă«äŒŒăŠăăŠăé䌎ăźćŻŸă«æăĄäžăăăăăźăŻăăăźćéĄăć
šăŠăźD ăźćŻŸè±Ąă«ă€ăăŠè§Łăæă€ăšăă§ăăăăŸăăăźăšăă«éă(C ăźćŻŸè±Ąă«ă€ăăŠăćæ§)ă
éąæF : C âD ăććć€ ăźçæčă§ăăăšăăăšăćć€ăźăăçæčăźć·Šé䌎ă§ăăăă€ăŸăăunităšcounităăšăă«ććă§ăăé䌎ă§ăăă
ć
šăŠăźé䌎ăF , G , Δ, ηăăŻăăéšććăźćć€æ§ăæĄćŒ”ăăăC ăźćŻŸè±ĄX ă§Î”X C ăźć
æșéšćć ăC 1 ăšăăăD ăźćŻŸè±ĄY ă§Î·Y D ăźć
æșéšććăD 1 ăšăăăăăźăšăăF ăšG ăăăăăD 1 ăš C 1 ă«ć¶éăăéąæăŻăăăăźéšććăźćć€ăźćè»ąăšăȘăŁăŠăăă
ăăźæćłă§ăé䌎ăŻäžèŹćăăă éć
ă§ăăăăăăăF ăźćłé(ă€ăŸăăéąæG ă§ăăŁăŠFG ă1D F ăźćłăŸăăŻć·Šé䌎ă«ăȘăăšăŻéăăȘăăé䌎ăŻ2æčćă« äžèŹćăăăéă§ăăă
ć
šăŠăźé䌎ăF , G , Δ, ηăăŻD ă«ăăăéąéŁăăăąăă ăT , η, ÎŒăă«æăĄäžăăăăšăă§ăăăéąæ
T
:
D
→ â -->
D
{\displaystyle T:{\mathcal {D}}\to {\mathcal {D}}}
ăŻT = GF ă§äžăăăăăăąăăăźunit
η η -->
:
1
D
→ â -->
T
{\displaystyle \eta :1_{\mathcal {D}}\to T}
ăŻé䌎ăźunit ηăăźăăźă§ăăăäčæłăźć€æ
μ ÎŒ -->
:
T
2
→ â -->
T
{\displaystyle \mu :T^{2}\to T\,}
ăŻÎŒ = G ΔF ă§äžăăăăăććŻŸçă«ăăFG , Δ, F ηG ăăŻC ă«ăăăăłăąăă ăćźăăă
ć
šăŠăźăąăăăé䌎ăăäœăăăšăă§ăăăćźéăć
žćçăȘăąăăăŻć€ăăźé䌎ăăäžăźæčæłăçšăăŠæ§æăăăŠăăă2ă€ăźæ§æEilenbergâMoore algebra ăšăŻă©ă€ăčăȘć ăŻăąăăăăé䌎ăæ§æăăćéĄă«ćŻŸăăă2ă€ăźäžĄæ„”ç«Żăźè§Łă§ăăă