連接層
|
Read other articles:

Taishi Ci Taishi Ci (166 - 206 M) adalah perwira militer negara Dong Wu pada Zaman Tiga Negara di Tiongkok dulu. Pada awalnya Taishi Ci bekerja di bawah Liu Yao tetapi kemudian melanggar kesetiaannya setelah Liu Yao menolak untuk memperhatikan nasihat strategi yang diajukan oleh Taishi Ci, kemudian dia melarikan diri ke daerah tetangga. Taishi Ci melarikan diri ke daerah Dangyang, suatu posisi daerah militer yang strategis dan penting sejak zaman Sun Tzu, disana dia mengangkat dirinya sebagai...

Artikel ini bukan mengenai Atambua (kota). Kota AtambuaKecamatanNegara IndonesiaProvinsiNusa Tenggara TimurKabupatenBeluPopulasi • Total30,254 jiwa (2.016)[1] jiwaKode pos85711 Kota Atambua85711 Tenukiik85712 Manumutin85718 FatubenaoKode Kemendagri53.04.12 Kode BPS5306060 Desa/kelurahanKota AtambuaTenukiikManumutinFatubenao Kota Atambua adalah sebuah Kecamatan di Kota Atambua, Kabupaten Belu, Nusa Tenggara Timur, Indonesia. Kecamatan ini merupakan kecamatan pusat akti...

Artikel ini bukan mengenai iftar. Kolak, kudapan umum yang sering dijadikan takjil Takjil adalah istilah umum untuk kudapan yang dimakan sesaat setelah berbuka puasa, biasanya berupa makanan manis seperti kolak pisang, sup buah, es campur, dan lain sebagainya. Dalam Kamus Besar Bahasa Indonesia (KBBI), kata takjil memiliki arti mempercepat dalam berbuka puasa.[1] Kata tersebut berakar dari kata 'ajila dalam bahasa Arab yang memiliki arti menyegerakan, sehingga takjil bermakna perintah...

Gentlemen of NerveCharles Chaplin, Mabel Normand dan Mack Swain dalam film Gentlemen of NerveSutradaraCharles ChaplinProduserMack SennettPemeranCharles Chaplin Mabel Normand Chester Conklin Mack Swain Phyllis Allen Edgar Kennedy Alice DavenportSinematograferFrank D. WilliamsPerusahaanproduksiKeystone StudiosDistributorMutual FilmTanggal rilis 29 Oktober 1914 (1914-10-29) Durasi16 menitNegaraAmerika SerikatBahasaAntarjudul Inggris Gentlemen of Nerve adalah sebuah film bisu komedi Amerika ...

Commune in Normandy, FranceBarbevilleCommuneBarbeville ChateauLocation of Barbeville BarbevilleShow map of FranceBarbevilleShow map of NormandyCoordinates: 49°16′32″N 0°44′52″W / 49.2756°N 0.7478°W / 49.2756; -0.7478CountryFranceRegionNormandyDepartmentCalvadosArrondissementBayeuxCantonBayeuxIntercommunalityBayeux IntercomGovernment • Mayor (2020–2026) Christian Viel[1]Area13.47 km2 (1.34 sq mi)Population (2021...

Tsuyama 津山市Kota BenderaLambangLokasi Tsuyama di Prefektur OkayamaNegara JepangWilayahChūgokuPrefektur OkayamaPemerintahan • Wali kotaKeizō TaniguchiLuas • Total506 km2 (195 sq mi)Populasi (Oktober 1, 2015) • Total103.746 • Kepadatan205,0/km2 (5,300/sq mi)Zona waktuUTC+9 (JST)Kode pos708-8501Simbol • PohonCinnamomum camphora• BungaRhododendron indicumPrunus serrulataNomor telepon0868-32-208...

Ismaël Bennacer Bennacer con il Milan nel 2022 Nazionalità Francia Algeria (dal 2016) Altezza 175 cm Peso 70 kg Calcio Ruolo Centrocampista Squadra Milan Carriera Giovanili 2004-2015 Arles-Avignon Squadre di club1 2014-2015 Arles-Avignon6 (0)2015-2017 Arsenal0 (0)2017→ Tours16 (1)2017-2019 Empoli76 (2)2019- Milan125 (5) Nazionale 2015 Francia U-184 (1)2015-2016 Francia U-197 (1)2016- Algeria48 (2) Palmarès Coppa d'Africa Oro Egitto 2...

English footballer Charles Buchan Buchan on a cigarette card issued in 1911Personal informationFull name Charles Murray BuchanDate of birth (1891-09-22)22 September 1891Place of birth Plumstead, London, EnglandDate of death 25 June 1960(1960-06-25) (aged 68)Place of death Monte Carlo, MonacoHeight 6 ft 1 in (1.85 m)[1]Position(s) Centre forwardSenior career*Years Team Apps (Gls)1909–1910 Woolwich Arsenal 0 (0)1910–1911 Leyton[2] 1911–1925 Sunderland 3...

МифологияРитуально-мифологическийкомплекс Система ценностей Сакральное Миф Мономиф Теория основного мифа Ритуал Обряд Праздник Жречество Мифологическое сознание Магическое мышление Низшая мифология Модель мира Цикличность Сотворение мира Мировое яйцо Мифическое �...
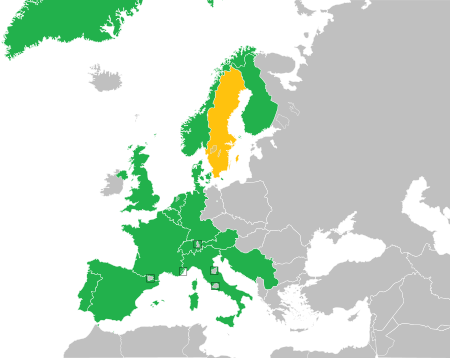
Kontes Lagu Eurovision 1964 Final 21 Maret 1964 Pembawa Acara Lotte Wæver Konduktor Kai Mortensen Penyiar Tuan Rumah DR Tempat Tivolis KoncertsalKopenhagen, Denmark Lagu pemenang ItaliaNon ho l'età Sistem pemberian suara Tiap negara mengirimkan 10 juri yang memberikan tiga poin kepada lagu favorit mereka nomor satu, dua, dan tiga. Poin kemudian dijumlahkan dan lagu urutan pertama, kedua, dan ketiga diberikan 5, 3, dan 1 poin secara berurutan. Jika hanya satu lagu yang dipilih semua j...

Prominent street in Yarmouth, Maine Princes Point RoadThe southern end of Princes Point at its intersection with (l-r) Morton Road, Old Town Landing Road and Sunset Point RoadLength1.93 mi (3.11 km)LocationYarmouth, Maine, U.S.Northern endLafayette Street (Maine State Route 88)Southern endSunset Point RoadConstructionCompletionc. 1780 (244 years ago) (1780) Princes Point Road is a prominent street in Yarmouth, Maine, United States. It runs for about 1.93 mile...

جمهورية مقدونيا الاشتراكية Социјалистичка Република Македонија جمهورية مكونة ليوغوسلافيا 1944 – 1991 جمهورية مقدونيا الاشتراكيةعلم جمهورية مقدونيا الاشتراكيةشعار مقدونيا داخل يوغوسلافيا عاصمة سكوبيه نظام الحكم جمهورية اشتراكية اللغة الرسمية الصربية الكرواتية...

County in Colorado, United States County in ColoradoRoutt CountyCountyEntering Routt County from the west on U.S. Route 40Location within the U.S. state of ColoradoColorado's location within the U.S.Coordinates: 40°29′N 106°59′W / 40.48°N 106.99°W / 40.48; -106.99Country United StatesState ColoradoFoundedJanuary 29, 1877Named forJohn Long RouttSeatSteamboat SpringsLargest citySteamboat SpringsArea • Total2,368 sq mi (6,130 k...

Disambiguazione – Se stai cercando altri significati, vedi Berlino (disambigua). Questa voce o sezione sull'argomento geografia ha problemi di struttura e di organizzazione delle informazioni. Motivo: La voce non risponde agli standard richiesti da Wikipedia:Modello di voce/Centro abitato nell'impostazione e nei contenuti. Risistema la struttura espositiva, logica e/o bibliografica dei contenuti. Nella discussione puoi collaborare con altri utenti alla risistemazione. Segui i suggerim...

约金·费舍尔·尼尔森Joachim Fischer Nielsen基本資料代表國家/地區 丹麦出生 (1978-11-23) 1978年11月23日(45歲)[1] 丹麦哥本哈根[1]身高1.88米(6英尺2英寸)[1]握拍左手[1]主項:混合雙打職業戰績117勝–61負(男單)133勝–40負(男雙)306勝–101負(混雙)最高世界排名第1位(混雙-C.彼德森)(2015年4月2日[2])現時世界排名第10位(混雙-C.彼德森�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2022) اِبْنُ زُهْرَةَ الإِمامُ إبنُ زُهرَةَ الحَلَبِيْ معلومات شخصية الميلاد 7 رمضان 511 هـ/2 يناير 1189مـحلب، بلاد الشام تاريخ الوفاة رجب 585 هـ/1189مـ (74 عاما) مكان الد�...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016) فيما يلي...

Medical school, hospital and public medical research university based in Lucknow, Uttar Pradesh Dr. Ram Manohar Lohia Institute of Medical SciencesMotto in EnglishMay All be HealthyTypeState universityEstablished2006 (18 years ago) (2006)Endowment₹324 crore (US$39 million) (2024-25) [1]ChairmanChief Secretary, Government of Uttar PradeshDirectorC.M. SinghLocationLucknow, Uttar Pradesh, IndiaCampusGomti Nagar, LucknowAffiliationsUniversity Grants CommissionWeb...

David AndersenAndersen saat bersama FC BarcelonaFree agentPosisiPower forward / CentreInformasi pribadiLahir23 Juni 1980 (umur 44)Melbourne, VictoriaKebangsaanAustralianTinggi6 ft 11 in (2,11 m)Berat250 pon (113 kg)Informasi karierSekolah menengah atasLake Ginninderra (Canberra, ACT)Draf NBA2002 / Babak: 2 / Urutan pemilihan: ke-37 secara keseluruhanDipilih oleh Atlanta HawksKarier bermain1998–sekarangRiwayat karier1998–1999Wollongong Hawks1999–2003Kinder B...

Special operations force of the Pakistan Army This article is about the Pakistan Army's special operations force. For the Pakistan Navy's special force of the same name, see Special Service Group (Navy). For other similarly named organizations, see Special service (disambiguation). Special Service GroupActiveMarch 23, 1956; 68 years ago (1956-03-23)Country PakistanBranch Pakistan ArmyTypeSpecial forcesRole Special operations Counter-terrorism Unconventional warfare...












