レピュニット
|
Read other articles:

Proposed rail undersea tunnel Helsinki–Tallinn TunnelA map of the assessed tunnel routes between Tallinn and HelsinkiOverviewLocationGulf of Finland (Baltic Sea)StatusPlannedStartÜlemiste, EstoniaEndPasila, Helsinki, FinlandTechnicalNo. of tracks2Track gauge1,435 mm (4 ft 8+1⁄2 in) (standard gauge) The tunnel in the context of the larger Rail Baltica project The Helsinki–Tallinn Tunnel is a proposed undersea tunnel that would span the Gulf of Finland and connect...

American abolitionist (1805–1875)[ Ann Carroll Smith (née Fitzhugh; 1805–1875)[1] was an American abolitionist, mother of Elizabeth Smith Miller, and the spouse of Gerrit Smith. Her older brother was Henry Fitzhugh. Ann and Gerrit Smith's Peterboro, New York, home was a station on the Underground Railroad. Known as Nancy,[2] Ann Fitzhugh Smith frequently traveled via an enclosed carriage to permit her carriage to be used, in her absence, to convey veiled fugitives on thei...
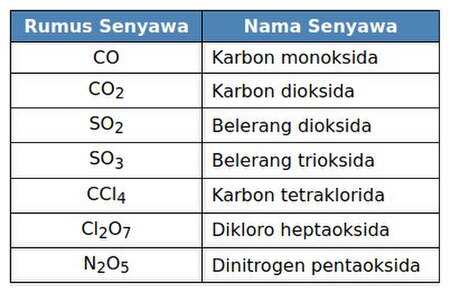
Tata nama senyawa kimia adalah serangkaian aturan persenyawaan kimia yang disusun secara sistematis. Tata nama kimia disusun berdasarkan aturan IUPAC (International Union of Pure and Applied Chemistry). Senyawa ionik Berkas:Wikiyoen.jpgContoh penamaan senyawa ionik Senyawa ionik terbentuk dari kation (ion positif) dan anion (ion negatif). Kebanyakan senyawa ionik merupakan senyawa biner, yaitu senyawa yang terbentuk hanya dari dua unsur. Untuk senyawa ionik biner, penamaan dimulai dari kation...

Festival Internacional de Cine Erótico de Barcelona País Espanha Página oficial Uma dançarina no FICEB 2006 O Festival Internacional de Cine Erótico de Barcelona (FICEB) é um festival anual e cerimônia de premiação do cinema pornográfico espanhol. O evento começou em 1993 com o objetivo de dinamizar e normalizar a indústria do sexo na Espanha. Desde 1997 tem sido realizado no centro de convenções La Farga em L'Hospitalet de Llobregat, uma cidade nos arredores de Barcelona.[1] Em...

مونتالدو بورميدا الإحداثيات 44°41′01″N 8°35′20″E / 44.683611111111°N 8.5888888888889°E / 44.683611111111; 8.5888888888889 [1] تقسيم إداري البلد إيطاليا[2] التقسيم الأعلى مقاطعة ألساندريا خصائص جغرافية المساحة 5.72 كيلومتر مربع (9 أكتوبر 2011)[3] ارتفاع 334 متر ع

Penyuntingan Artikel oleh pengguna baru atau anonim untuk saat ini tidak diizinkan.Lihat kebijakan pelindungan dan log pelindungan untuk informasi selengkapnya. Jika Anda tidak dapat menyunting Artikel ini dan Anda ingin melakukannya, Anda dapat memohon permintaan penyuntingan, diskusikan perubahan yang ingin dilakukan di halaman pembicaraan, memohon untuk melepaskan pelindungan, masuk, atau buatlah sebuah akun. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon...

Harvey WeinsteinWeinstein in April 2011Lahir19 Maret 1952 (umur 71)Kota New York, New York, U.S.PekerjaanProduser filmTahun aktif1979–2017Suami/istriEve Chilton (m. 1987; c. 2004) Georgina Chapman (m. 2007; sep. 2017)Anak5 Harvey Weinstein (/ˈwaɪnstiːn/; lahir 19 Maret 1952) merupakan mantan produser film berkebangsaan Amerika Serikat. Dia dan saudaranya Bob Weinstein ikut me...

Dieser Artikel beschreibt den Musiker. Ein Artikel über den Regisseur Jörg Michael befindet sich unter dessen bürgerlichem Namen Jürgen Enz. Jörg Michael, 2009 Jörg Michael (* 27. März 1963 in Dortmund) ist ein deutscher Heavy-Metal-Schlagzeuger. In seiner über 25-jährigen Karriere spielte er u. a. in den Bands Grave Digger, Rage, Mekong Delta, Axel Rudi Pell, Running Wild und Saxon. Von 1996 bis 2012 spielte er fest in der finnischen Formation Stratovarius. Michaels Schlagzeug beste...

ДостопримечательностьЗдание бывшего духовного училищабелор. Будынак былога духоўнага вучылішча 52°25′40″ с. ш. 31°01′09″ в. д.HGЯO Страна Белоруссия Город Гомель Архитектурный стиль классицизм Архитектор Джон Кларк[be] Строительство 1799—1819 годы Медиафайл...

This article is part of a series on theState governments of the United States State constitution Comparison Statehouse Executive State executives Governor (List) Other common officials: Attorney general Auditor/Comptroller Lieutenant governor Secretary of state Treasurer Agriculture commissioner List of statewide elected officials Legislative State representatives (Alabama to Missouri, Montana to Wyoming) State senators List of legislatures Judiciary State supreme court State court Local offi...

Mayor Jenderal TNI (Purn.)Mohammad MunibS.I.P.Pa Sahli Tk. III Kasad bidang PolkamnasMasa jabatan25 Februari 2022 – 27 Juni 2022PendahuluDwi Jati UtomoPenggantiJunaediKepala Pusat Zeni Angkatan Darat ke-1Masa jabatan9 April 2020 – 25 Februari 2022PendahuluTidak ada, Jabatan baruPenggantiAby Ismawan Informasi pribadiLahir29 Juli 1964 (umur 59)Kebumen, Banyubiru, Semarang, Jawa TengahSuami/istriDayana MunibAlma materAkademi Militer (1987)Karier militerPihak I...

У Вікіпедії є статті про інші громади з назвою: Іванівська селищна громада. Іванівська селищна громадаОсновні даніКраїна УкраїнаОбласть Одеська областьРайон Березівський районКод КАТОТТГ UA51020090000073639Утворена 22 грудня 2019 рокуАдмін. центр ІванівкаТериторія та населе�...

Association football club in Pristina, Kosovo KF Prishtina redirects here. Football clubPrishtinaFull nameFootball Club PrishtinaNickname(s)Plisat (The Clods)Short namePRI or FCPFounded1922; 101 years ago (1922), as KosovaGroundFadil Vokrri StadiumCapacity13,980OwnerRemzi Ejupi (50%)Rahman Haradini (50%)ChairmanHakif GashiManagerNdubuisi EgboLeagueKosovo Superleague2022–23Kosovo Superleague, 5th of 10WebsiteClub website Home colours Away colours Current season Football Clu...

Former music venue in Denver, Colorado 1601 W. Evans Ave, Denver, CO, 80223. Home of the Family Dog Denver, 1967-1968 The Family Dog DenverThe Dog, The Denver DogFull nameThe Family Dog DenverLocation1601 West Evans AvenueDenver, ColoradoCoordinates39°40′43.22″N 105°0′23.64″W / 39.6786722°N 105.0065667°W / 39.6786722; -105.0065667OwnerChet Helms, Bob Cohen, Barry FeyOpenedSeptember 8, 1967ClosedJuly 19, 1968 The Family Dog Denver (also known as The Family D...

American politician Sherman LelandPresident of the Massachusetts SenateIn office1828–1829Preceded byJohn MillsSucceeded bySamuel LathropMember of theMassachusetts SenateNorfolk County District[1]In office1828[1]–1829[1]Member of theMassachusetts SenateNorfolk County District[1]In office1823[1]–1824[1]Member of theMassachusetts Constitutional Convention of 1820[2]In office1820[2]–1820[2]Member of theMassachusetts H...

Editing an entry of the NOED using LEXX LEXX is a text editor which was possibly the first to use live parsing and colour syntax highlighting. It was written by Mike Cowlishaw of IBM in 1985. The name was chosen because he wrote it as a tool for lexicographers, during an assignment for Oxford University Press's 'New Oxford English Dictionary' (NOED; the second edition of the Oxford English Dictionary).[1] The program ran (and still, in 2018, runs[2]) on mainframes under VM/CMS...

Volleyball events were contested at the 1998 Central American and Caribbean Games in Maracaibo, Venezuela. Medal summary Event Gold Silver Bronze Men’s tournament CubaYosenki GarcíaAlain RocaÁngel DennisIhosvany HernándezRaúl DiagoNicolás VivesAlexeis ArgilagosIván RuizOsvaldo HernándezPavel PimientaRamón GatoRodolfo Sánchez MexicoGerardo ContrerasLuis ContrerasCarlos CoronatoJuan GarcíaAlejandro GutiérrezJosé MartellGerardo MartínezVíctor PurataIgnacio RamírezJes...

Rugby playerVirimi VakatawaVakatawa with Racing 92 in 2012Birth nameVirimi VakatawaDate of birth (1992-05-01) 1 May 1992 (age 31)Place of birthRangiora, New ZealandHeight1.86 m (6 ft 1 in)[1]Weight99 kg (218 lb)[1]Rugby union careerPosition(s) Centre, Wing[1]Current team Bristol BearsYouth career2010–2011 Naluwai RC[2]Nasinu Secondary School[2]Racing 92[3]Senior careerYears Team Apps (Points)2011–2013 Racing 92 ...

American actress This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Daniela Nieves – news · newspapers · books · scholar · JSTOR (October 2015) (Learn how and when to remove this template message) ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada 2014. Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti m...




