Taxicab geometry
|
Read other articles:

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) Artikel ini berisi konten yang ditulis dengan gaya sebuah iklan. Bantulah memperbaiki artikel ini dengan menghapus konten yang dianggap sebagai spam dan pranala luar yang tidak sesuai, dan tambahkan konten ensiklopedis yang ditulis dari sudut pandang netral dan sesuai dengan kebijakan ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Портрет императора Луция Вера как арвальского брата (около 160 года н. э.) Арва́льские бра́тья (лат. Fratres Arvales, «бра́тья-па́хари» от лат. arvum — пашня) — римская коллегия 12 жрецов. В обязанности её входили молитвы богам о ниспослании урожая и процветании общины гр�...

Danau BaturDanau BaturLetakKintamani, Kabupaten Bangli, Bali, IndonesiaKoordinat08°15′30″S 115°24′30″E / 8.25833°S 115.40833°E / -8.25833; 115.40833Koordinat: 08°15′30″S 115°24′30″E / 8.25833°S 115.40833°E / -8.25833; 115.40833Jenis perairanPolimiktik, danau kawahPanjang maksimal2,5 km (1,6 mi)Lebar maksimal7,5 km (4,7 mi)Area permukaan15,9 km2 (3.900 ekar)Kedalaman maksimal88 m (289 ft)...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Lazimi atau wirid lazim (Arab: الْوِرْدُ اللَّازِمُcode: ar is deprecated ) adalah litani biasa yang dipraktikkan oleh para pengikut dalam sufisme di tarekat Tijaniyah. Praktiknya diadakan secara individu.[1][2] Prese...
Daftar keuskupan di Amerika adalah sebuah daftar yang memuat dan menjabarkan pembagian terhadap wilayah administratif Gereja Katolik Roma yang dipimpin oleh seorang uskup ataupun ordinaris di Benua Amerika. Konferensi para uskup Amerika Latin bergabung dalam Konferensi Waligereja Amerika Latin.[1] Amerika Serikat Artikel utama: Daftar keuskupan di Amerika Serikat Provinsi Gerejawi Anchorage Keuskupan Agung Anchorage Keuskupan Fairbanks Keuskupan Juneau Provinsi Gerejawi Atlanta Keusku...

2010 single by Enrique Iglesias HeartbeatSingle by Enrique Iglesias featuring Nicole Scherzingerfrom the album Euphoria Released8 June 2010 (2010-06-08)Recorded2009StudioSouth Point (Miami, Florida)GenreElectropop[1]Length4:15 (album version)3:50 (radio edit)LabelUniversal RepublicSongwriter(s)Enrique IglesiasJamie ScottMark TaylorProducer(s)Mark TaylorEnrique Iglesias singles chronology I Like It (2010) Heartbeat (2010) No Me Digas Que No (2010) Nicole Scherzinger&...
Strada R504 KolymaLocalizzazioneStato Russia Circondari federaliSacha-Jacuzia Soggetti federaliOblast' di Magadan DatiClassificazionestrada federale InizioNižnij Bestjach FineMagadan Lunghezza2.036 km Data apertura2008 Percorso Manuale Il ponte sulla Kolyma La strada R504 «Kolyma», nota anche come strada delle Ossa, è una strada federale russa di collegamento fra le città di Magadan, sul mare di Ochotsk, e Nižnij Bestjach, situata sulla riva orientale della Lena di fronte a Jakutsk...

Safita (ar) صافيتا Administration Pays Syrie Muhafazah (محافظة) Tartous Démographie Population 32 213 hab. (2009) Géographie Coordonnées 34° 49′ 00″ nord, 36° 07′ 00″ est Altitude 303 m Localisation Géolocalisation sur la carte : Syrie Safita modifier La ville de Safita (صافيتا en arabe) est située au nord-ouest de la Syrie actuelle, plus précisément au sud-est de Tartous et au nord-ouest du Krak des C...

Olympic gymnastics event Men's vaultat the Games of the XXII OlympiadNikolai Andrianov (c. 1974)VenueLuzhniki Palace of SportsDate20–25 JulyCompetitors65 from 14 nationsWinning score19.825Medalists Nikolai Andrianov Soviet Union Alexander Dityatin Soviet Union Roland Brückner East Germany← 19761984 → Gymnastics at the1980 Summer OlympicsList of gymnastsArtisticTeam all-aroundmenwomenIndividual all-aroundmenwomenVaultmenwomenFloormenwomenPommel...

2015 concert tour by Robbie Williams Let Me Entertain You TourTour by Robbie WilliamsPromotional poster for the tourStart date25 March 2015End date3 November 2015Legs4No. of shows28 in Europe2 in Asia12 in Australia42 totalRobbie Williams concert chronology Swings Both Ways Live(2014) Let Me Entertain You Tour(2015) The Heavy Entertainment Show Tour(2017–18) The Let Me Entertain You Tour[1] was the eleventh concert tour by English recording artist, Robbie Williams. The tour began in...

Rodellocomune Rodello – VedutaVista di Rodello LocalizzazioneStato Italia Regione Piemonte Provincia Cuneo AmministrazioneSindacoFranco Aledda (lista civica) dal 26-5-2014 TerritorioCoordinate44°37′42.74″N 8°03′24.62″E / 44.62854°N 8.056838°E44.62854; 8.056838 (Rodello)Coordinate: 44°37′42.74″N 8°03′24.62″E / 44.62854°N 8.056838°E44.62854; 8.056838 (Rodello) Altitudine537 m s.l.m. Superficie8,9 ...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Kontributor utama artikel ini tampaknya memiliki hubungan dekat dengan subjek. Artikel ini mungkin perlu dirapikan agar mematuhi kebijakan konten Wikipedia, terutama dalam hal sudut pandang netral. Silakan dibahas lebih lanjut di halaman pembicaraan artikel ini. (July 2017) (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Vossloh AGJenisAktiengesellschaftKode emitenFWB: VOSIndustriInfrastruktur relDidirikan1888PendiriEduard VosslohKantorpusatWerdohl, JermanTokohkunciAndreas...

Perang BoshinSamurai klan Satsuma, bertempur di pihak kekaisaran semasa Perang Boshin. Foto: Felice Beato.TanggalJanuari 1868 – Mei 1869LokasiJepangHasil Keshogunan Tokugawa berakhir;kembalinya kekuasaan di tangan kekaisaranPihak terlibat Kekaisaran Jepang Keshogunan Tokugawa Republik EzoTokoh dan pemimpin Pemimpin: Kaisar Meiji,Panglima: Saigō Takamori,AD: Kuroda Kiyotaka Keshogunan:Pemimpin: Tokugawa Yoshinobu,AD: Katsu Kaishu,AL: Enomoto Takeaki,Republik Ezo:Presiden:Enomoto Takeaki,Pan...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The article's lead section may need to be rewritten. Please help improve the lead and read the lead layout guide. (June 2013) (Learn how and when to remove this message) This article needs to be updated. Please help update this article to reflect recent events or newly available information. (June 2013) This article needs additional citatio...
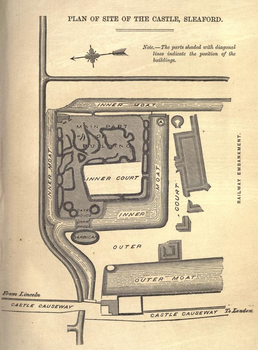
Market town and civil parish in Lincolnshire, England This article is about the town in Lincolnshire. For other uses, see Sleaford (disambiguation). Town and civil parish in EnglandSleafordTown and civil parishClockwise from top: Aerial of Sleaford Castle site, Handley Monument, St Deny's Church, view across rooftops of Sleaford and Sessions House (on the right)SleafordLocation within LincolnshirePopulation19,807 (2021 Census)[1]OS grid referenceTF064455• London1...

مجلة Forza MilanForza Milan! (بالإيطالية)[1] معلومات عامةالنوع مجلة رياضيةبلد المنشأ إيطاليا[1] التأسيس 1968 الاختفاء 2018 الثمن 3.5 € 34.99 € (اشتراك سنوي)شخصيات هامةرئيس التحرير فابريتسيو ميليجارييجوالتحريراللغة الإيطاليةالمواضيع كرة القدم الإدارةالمقر الرئيسي ميلانو، إيطال...

Cet article est une ébauche concernant l’histoire et la Syrie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Ne doit pas être confondu avec Djébel el-Druze. État des Druzes جبل الدروز 1921–1936 La Syrie mandataire. L'État des Druzes est en bleu.Informations générales Statut Mandat de la SDN pour la France Capitale Soueïda Langue(s) Français et arabe Religion Druze 84,8%Chrétien 13,8%Isla...
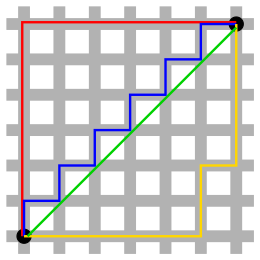


















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)






















