Unit sphere
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Shadow of the Thin ManPoster rilis teatrikalSutradaraW. S. Van DykeProduserHunt StrombergDitulis olehDashiell Hammett (para karakter)Skenario Harry Kurnitz Irving Brecher CeritaHarry KurnitzPemeran William Powell Myrna Loy Penata musikDavid SnellSinematograferWilliam H. DanielsPenyuntingRobert J. KernPerusahaanproduksiMetro-Goldwyn-MayerDistributorMetro-Goldwyn-MayerTanggal rilis 21 November 1941 (1941-11-21) (US) Durasi97 menitNegaraAmerika SerikatBahasaInggrisAnggaran$821.000...
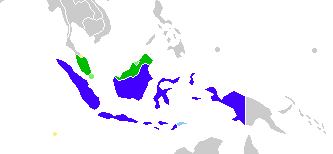
Berikut adalah daftar negara berdaulat dengan bahasa Melayu berstatus sebagai bahasa resmi. Linguasfer Melayu. Indonesia Malaysia Singapura dan Brunei, di mana bahasa Melayu Baku adalah bahasa resmi Timor Leste, di mana bahasa Indonesia adalah bahasa kerja Thailand Selatan dan Kep. Cocos, di mana varietas Melayu lainnya dituturkan Negara berdaulat Negara di mana bahasa Melayu merupakan bahasa resmi de jure Negara Wilayah Populasi1 Ba...

New York City Subway station in Brooklyn New York City Subway station in Brooklyn, New York High Street New York City Subway station (rapid transit)Station curvatureStation statisticsAddressHigh Street & Cadman Plaza EastBrooklyn, NY 11201BoroughBrooklynLocaleBrooklyn Heights, DUMBO, Downtown BrooklynCoordinates40°41′56″N 73°59′23″W / 40.69889°N 73.98972°W / 40.69889; -73.98972DivisionB (IND)[1]Line IND Eighth...

American politician & author (born 1960) This article is about the author and politician. For other people with the same name, see Chris Stewart. Chris StewartMember of the U.S. House of Representativesfrom Utah's 2nd districtIn officeJanuary 3, 2013 – September 15, 2023Preceded byJim MathesonSucceeded byCeleste Maloy Personal detailsBornChristopher Douglas Stewart (1960-07-15) July 15, 1960 (age 63)Logan, Utah, U.S.Political partyRepublicanSpouseEvie StewartRe...

Цилиндрический съемный ферритовый фильтр Съемный ферритовый фильтр в форме параллелепипеда Ферритовый фильтр в виде цилиндра без пластмассового покрытия. Характеристика кривой импеданса. Z {\displaystyle {\text{Z}}} — полное сопротивление; X L {\displaystyle {\text{X}}_{\text{L}}} — реактивная со�...

Pathological, often painful, involuntary muscle contraction For other uses, see Cramp (disambiguation). Not to be confused with Seizure or Spasm. Medical conditionCrampSymptomssudden muscle pain and a paralysis-like immobilityTreatmentquinine, stretching, massage, and drinking liquids A cramp is a sudden, involuntary, painful skeletal muscle contraction[1][2] or overshortening associated with electrical activity;[3] while generally temporary and non-damaging, they can ...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Ця стаття є сирим перекладом з іншої мови. Можливо, вона створена за допомогою машинного перекладу або перекладачем, який недостатньо володіє обома мовами. Будь ласка, допоможіть поліпшити переклад. (березень 2012) Рейтинг свободи преси Хоча свобода преси в Україні ніко�...

Antimon triselenida Nama Nama lain antimonselit selenoksiantimon Penanda Nomor CAS 1315-05-5 Y Model 3D (JSmol) Gambar interaktif 3DMet {{{3DMet}}} ChemSpider 11483776 Y Nomor EC PubChem CID 6391662 Nomor RTECS {{{value}}} CompTox Dashboard (EPA) DTXSID30895002 InChI InChI=1S/2Sb.3Se/q2*+3;3*-2 YKey: WWUNXXBCFXOXHC-UHFFFAOYSA-N YInChI=1S/2Sb.3Se/q2*+3;3*-2Key: WWUNXXBCFXOXHC-UHFFFAOYSA-N SMILES [SbH3+3].[SbH3+3].[Se-2].[Se-2].[Se-2] Sifat Rumus kimia Sb2Se3 ...

Mexican football club Football clubVeracruz SportingFull nameVeracruz Sporting ClubNickname(s)Sporting, VeracruzFounded1908GroundEstadio de la Universidad UVM Villa RicaManager Arturo AvilésLeagueTercera División de México Home colours Away colours Veracruz Sporting Club is a Mexican football team from Veracruz, Veracruz State, playing in the Tercera División de México. They were one of Liga MX's inaugural members. History The club was founded in 1908 by the native Spaniards living in Ve...

У этого термина существуют и другие значения, см. Ярус. Крючки собранного яруса, используемого для лова рыбы Я́рус — крючковое орудие лова — особая разновидность гигантского перемёта, используемая в рыболовстве при океаническом или прибрежном морском лове разреж�...

مستر أولمبيا 1991 معلومات عامة فترة الانعقاد 13 - 15 سبتمبر 1991 مكان الانعقاد أورلاندو، فلوريدا، الولايات المتحدة المنظم الاتحاد الدولي لكمال الأجسام واللياقة البدنية (IFBB) المنطقة العالم ترتيب النسخة 27 الموقع الرسمي الموقع الرسمي لمحترفي اتحاد IFBB قائمة الفائزين صاحب ال...

Process of virus reproduction Not to be confused with Lytic cycle. Lysogenic cycle, compared to lytic cycle Lysogenic Cycle:1. The prokaryotic cell is shown with its DNA, in green. 2. The bacteriophage attaches and releases its DNA, shown in red, into the prokaryotic cell. 3. The phage DNA then moves through the cell to the host's DNA. 4. The phage DNA integrates itself into the host cell's DNA, creating prophage. 5. The prophage then remains dormant until the host cell divides. 6. After the ...

Albertville 1992 XVI Juegos Olímpicos de InviernoLocalización Albertville FranciaParticipantes • Países • Deportistas 64 países1801 atletasEventos 57 en 7 deportesCeremoniasApertura 8 de febrero de 1992Clausura 23 de febrero de 1992Inaugurado por François MitterrandJuramentos • Deportista • Juez Surya BonalyPierre BornatLlama olímpica Michel PlatiniFrançois-Cyrille GrangeEstadio olímpico Théâtre des CérémoniesCronología C...

Naval warfare conducted by submarines You can help expand this article with text translated from the corresponding article in German. (September 2023) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not trans...

هذه المقالة بحاجة لمراجعة خبير مختص في مجالها. يرجى من المختصين في مجالها مراجعتها وتطويرها. (أغسطس 2014) جماعات دغمش المسلحة هي مليشيات عائلية مسلحة فلسطينية في قطاع غزة، مرتبطة ببعض من قيادة حركة فتح على رأسهم محمد دحلان، ذات إمكانات تسلحية وتدريبية عالية باعتمادها على أفر...

Youth wings of political parties in Albania For other uses, see Bashkimi (disambiguation). This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2023) (Learn how and when to remove this message) Labour Youth Union of AlbaniaAlbanian: Bashkimi i Rinisë së Punës së ShqipërisëFoundedNovember 23, 1941Dissolved1991Headquart...

Sustained, long-term downturn in economic activity in one or more economies The examples and perspective in this article deal primarily with the English-speaking world and do not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (October 2012) (Learn how and when to remove this message) An economic depression is a period of carried long-term economic downturn that is the result of lowered econo...















![{\displaystyle V_{n}={\frac {\pi ^{n/2}}{\Gamma (1+n/2)}}={\begin{cases}{\pi ^{n/2}}/{(n/2)!}&\mathrm {if~} n\geq 0\mathrm {~is~even} \\[6mu]{2(2\pi )^{(n-1)/2}}/{n!!}&\mathrm {if~} n\geq 0\mathrm {~is~odd,} \end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf208735d51b452fb423a2e121ada1e6c269bf9)


![{\displaystyle A_{n-1}=nV_{n}={\frac {n\pi ^{n/2}}{\Gamma (1+n/2)}}={\frac {2\pi ^{n/2}}{\Gamma (n/2)}}={\begin{cases}{2\pi ^{n/2}}/{(n/2-1)!}&\mathrm {if~} n\geq 1\mathrm {~is~even} \\[6mu]{2(2\pi )^{(n-1)/2}}/{(n-2)!!}&\mathrm {if~} n\geq 1\mathrm {~is~odd.} \end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef608cca0068ac18865a9203858bacc8780fe7ac)

![{\displaystyle [-1,1]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2016a25b4496666df761c56045fc221d3fbd2c08)















































![{\displaystyle [-1,1]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a008254b1bf6d63ac3b13548c4c31180bcd43de)


















