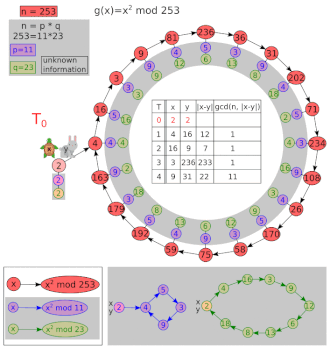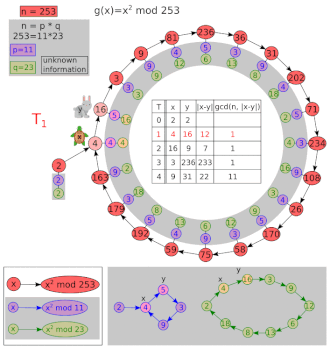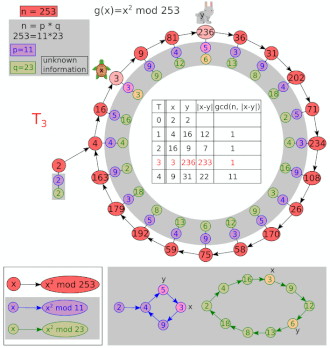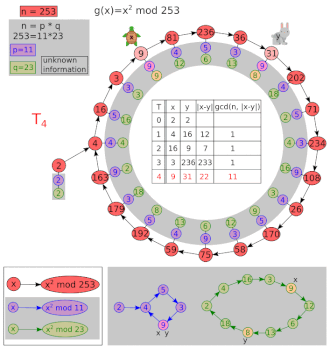
Pollard's rho algorithm
|
Read other articles:

American Airlines Flight 11Jalur penerbangan AA 11 dari Boston ke New York CityRingkasan pembajakanTanggal11 September 2001RingkasanPembajakan bunuh diriLokasiWorld Trade CenterPenumpang81 (termasuk 5 pembajak)Awak11TewasSeluruh 92 orang di pesawat, dan sekitar 1.600 orang (termasuk pelompat dan pekerja darurat) di Menara Utara World Trade Center.Selamat0Jenis pesawatBoeing 767-223EROperatorAmerican AirlinesRegistrasiN334AAAsalBandar Udara Internasional LoganTujuanBandar Udara Internasio...
مقاطعة أودوبون الإحداثيات 41°41′05″N 94°54′29″W / 41.684722222222°N 94.908055555556°W / 41.684722222222; -94.908055555556 [1] تاريخ التأسيس 1851 سبب التسمية جون جيمس أودوبون تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى آيوا العاصمة أودوبون التقسيمات �...

Anthony Šerić Informasi pribadiTanggal lahir 15 Januari 1979 (umur 45)Tempat lahir Sydney, AustraliaTinggi 1,81 m (5 ft 11+1⁄2 in)Posisi bermain BekInformasi klubKlub saat ini KarabüksporNomor 20Karier junior AIS CanberraKarier senior*Tahun Tim Tampil (Gol)1997–1999 Hajduk Split 33 (0)1999–2001 Parma 0 (0)1999–2001 → Verona (pinjam) 22 (1)2001–2005 Verona 25 (0)2002–2003 → Brescia (pinjam) 30 (1)2003–2004 → Parma (pinjam) 17 (0)2004–2005 → L...

United States Navy SEALsLambang Special Warfare atau SEAL Trident.Aktif1 Januari 1962 – sekarangNegara Amerika SerikatCabang Angkatan Laut Amerika SerikatTipe unitPasukan operasi khususSEa, Air, LandPeranTugas utama: Aksi langsung Pengintaian khusus Pertahanan internal asing Penanggulangan terorisme Perang tidak konvensional Peran lain: Operasi anti-narkoba Pemulihan personel Pengintaian hidrografi Bagian dari Komando Perang Khusus Angkatan Laut Amerika Serikat Komando Operasi Khusus A...

Louis-Marie de La Révellière-LépeauxPotret karya Gerard van Spaendonck pada sekitar tahun 1797 Informasi pribadiLahir(1753-08-24)24 Agustus 1753Montaigu, VendéeMeninggal24 Maret 1824(1824-03-24) (umur 70)MakamPemakaman Père LachaiseKebangsaanPrancisPekerjaanPengacaraDikenal karenaKonvensi Nasional; Direktori PrancisSunting kotak info • L • B Louis Marie de La Révellière-Lépeaux (24 Agustus 1753 – 24 Maret 1824) adalah seorang deputi untuk Konvensi Na...

National Olympic Committee Guatemalan Olympic CommitteeCountry/Region GuatemalaCodeGUACreated1947Recognized1947ContinentalAssociationPASOHeadquartersGuatemala City, GuatemalaPresidentGerardo Rene Aguirre OestmannSecretary GeneralJuan Carlos Sagastume BendañaWebsitewww.cog.org.gt The Guatemalan Olympic Committee (Spanish: Comité Olímpico Guatemalteco, abbreviated as COG) is a non-profit organization serving as the National Olympic Committee of Guatemala and a part of the International ...
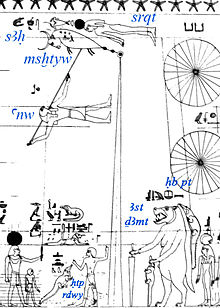
Celestial diagram in ancient Egyptian tomb Top and bottom portions[1] Astronomical ceiling decoration in its earliest form can be traced to the Tomb of Senenmut (Theban tomb no. 353), located at the site of Deir el-Bahri, discovered in Thebes, Upper Egypt. The tomb and the ceiling decorations date back to the XVIII Dynasty of ancient Egypt (circa 1479–1458 BCE). It is closed to the public.[2] Discovery The tomb of Senemut was discovered during the 1925–1927 excavations dir...

Годы 1712 · 1713 · 1714 · 1715 — 1716 — 1717 · 1718 · 1719 · 1720 Десятилетия 1690-е · 1700-е — 1710-е — 1720-е · 1730-е Века XVII век — XVIII век — XIX век 2-е тысячелетие XVI век XVII век XVIII век XIX век XX век 1690-е 1690 1691 1692 1693 1694 1695 1696 1697 1698 1699 1700-е 1700 1701 1702 1703 1704 1705 1706 1707 1708 1709 1710-е 1710 1711 1712 1713 1714 1715 17...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

This article contains Thai text. Without proper rendering support, you may see question marks, boxes, or other symbols instead of Thai script. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Traditional Thai musical instruments – news · newspapers · books · scholar · JSTOR (March 2021) (Learn how and wh...

منتخب لاتفيا لهوكي الجليد للناشئين البلد لاتفيا رمز IIHF LAT مشاركة دولية لاتفيا 47 – 1 اليونان (ريغا، لاتفيا؛ 10 نوفمبر 1992) أكبر فوز لاتفيا 47 – 1 اليونان (ريغا، لاتفيا؛ 10 نوفمبر 1992) أكبر هزيمة كندا 16 – 0 لاتفيا (ساسكاتون، ساسكاتشوان، كندا؛ 26 ديسمبر 2009) بطولة...

الضحاك بن مزاحم معلومات شخصية الميلاد القرن 7 ولاية بلخ الوفاة 102 هـ أو 105 هـ أو 106 هـخراسان الكبرى الإقامة خراسان الكبرىسمرقندمرو الشاهجان الكنية أبو القاسم أو أبو محمد اللقب الهلالي الخراساني أقرباء أخو محمد بن مزاحم، ومسلم بن مزاحم الحياة العملية الطبقة الط...
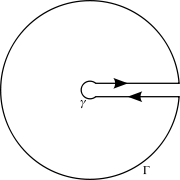
Method of evaluating certain integrals along paths in the complex plane This article is about the line integral in the complex plane. For the general line integral, see Line integral. Part of a series of articles aboutCalculus ∫ a b f ′ ( t ) d t = f ( b ) − f ( a ) {\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)} Fundamental theorem Limits Continuity Rolle's theorem Mean value theorem Inverse function theorem Differential Definitions Derivative (generalizations) Dif...

Computer program which translates code from one programming language to another This article is about software to translate computer languages. For the manga, see Compiler (manga). Compile and Compiling redirect here. For the software company, see Compile (company). For other uses, see Compilation. Program execution General concepts Code Translation Compiler Compile time Optimizing compiler Intermediate representation (IR) Execution Runtime system Runtime Executable Interpreter Virtual machin...

Colombian physicist (born c. 1976) Ana Maria ReyRey in 2014Born1976 or 1977 (age 46–47)Bogotá, ColombiaAlma materUniversidad de los Andes, University of MarylandChildren1[2]AwardsMacArthur Fellowship, Maria Goeppert-Mayer Award, Hispanic Engineer National Achievement Award, Blavatnik Award for Young ScientistsScientific careerInstitutionsUniversity of Colorado Boulder, National Institute of Standards and TechnologyThesisUltracold bosonic atoms loaded in optica...

Former free newspaper in Australia mXTypeFree daily newspaperFormatTabloidOwner(s)News Corp AustraliaPublisherTamara OppenEditorMelbourne: Craig HerbertSydney: Melissa MathesonBrisbane: Emma WardillFounded6 February 2001Ceased publication12 June 2015HeadquartersMelbourne, AustraliaWebsitewww.mx.net.au mX was an Australian free afternoon daily newspaper in the cities of Melbourne, Sydney and Brisbane, owned and produced by News Corp Australia. Targeted at commuters, its main channels of distri...

У этого термина существуют и другие значения, см. Братский район. район[1] / муниципальный район[2]Братский район Флаг 56° с. ш. 102° в. д.HGЯO Страна Россия Входит в Иркутскую область Адм. центр г. Братск Мэр Братского района Дубровин Александр Сергеевич Пр�...

يُشير الأدب التيلوغوي إلى الأعمال المكتوبة باللغة التيلوغوية، ويشمل ذلك القصائد، والقصص القصيرة، والروايات، والمسرحيات، والقصائد الغنائية، وغيرها. رغم دلالة بعض المؤشرات على أن تاريخ الأدب التيلوغوي يعود إلى منتصف الألف الأولى للميلاد، فإن تاريخ أول الأعمال الموجودة �...

English social reformer and arts patron 1718–1776 For the English duchess, see Elizabeth Montagu, Duchess of Manchester. For the British novelist, nurse, and art collector, see Lady Elizabeth Montagu. For the actress, née Montagu, see Elizabeth Varley. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Elizabeth Montagu – news ...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2019) قرن: قرن ...