Idempotence
|
Read other articles:

Puteri Indonesia PapuaLogo Puteri IndonesiaPembuatMooryati SoedibyoNegara asal Papua, IndonesiaRilisRilis asli1992 –SekarangPranala luarSitus web Puteri Indonesia Papua adalah sebuah kontes kecantikan yang ada di provinsi Papua, yang diadakan sejak tahun 1995 dengan nama provinsi Irian Jaya, dan pada tahun 2002 berubah menjadi Papua. Pemenang Puteri Indonesia Papua akan mewakili Papua pada kontes Puteri Indonesia, pemegang saat ini adalah Yunita Alanda Monim dari Kabupaten Jayapur...

2000 American filmBamboozledTheatrical release posterDirected bySpike LeeWritten bySpike LeeProduced byJon KilikSpike LeeStarring Damon Wayans Savion Glover Jada Pinkett Smith Tommy Davidson Michael Rapaport CinematographyEllen KurasEdited bySam PollardMusic byTerence BlanchardProductioncompany40 Acres and a Mule FilmworksDistributed byNew Line CinemaRelease date October 6, 2000 (2000-10-06) (United States) Running time135 minutesCountryUnited StatesLanguageEnglishBudget$10...
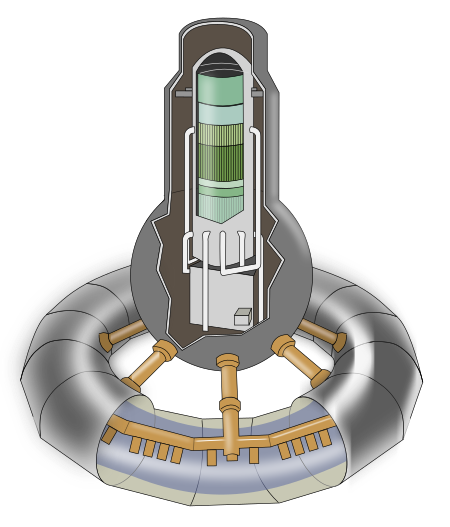
Type of commercial fission reactor This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: GE BWR – news · newspapers · books · scholar · JSTOR (January 2014) (Learn how and when to remove this template message) GE BWR(General Electric Boiling Water Reactor)GenerationGeneration I (BWR-1)Generation IIGeneration III (...

Inhaltsverzeichnis 1 Austragungsorte 2 Resultate 2.1 Frauen 2.1.1 Sprint 2.1.2 Keirin 2.1.3 Teamsprint 2.1.4 Mannschaftsverfolgung 2.1.5 Scratch 2.1.6 Punktefahren 2.1.7 Omnium 2.2 Männer 2.2.1 Sprint 2.2.2 Keirin 2.2.3 Teamsprint 2.2.4 Einerverfolgung 2.2.5 Mannschaftsverfolgung 2.2.6 Scratch 2.2.7 Punktefahren 2.2.8 Omnium 2.2.9 Zweier-Mannschaftsfahren 2.3 Teamwertung 3 Teamkürzel 4 Weblinks 5 Einzelnachweise Der UCI-Bahnrad-Weltcup 2015/16 wurde in drei Läufen zwischen November 2015 un...

У Вікіпедії є статті про інші значення цього терміна: Празький мир. Празький мир Тип мирна угода і договірПідписано 23 серпня 1866Місце ПрагаПідписанти Австрійська імперія і Королівство ПруссіяМови німецька Пра́зький мир (нім. Prager Frieden) — мирний договір між Австрі�...

The Church of Jesus Christ of Latter-day Saints in the United KingdomThe Preston England TempleAreaEurope NorthMembers186,933 (2022)[1]Stakes44Wards275Branches42Total Congregations[2]317Missions6Temples2 Operating1 Announced3 TotalFamily History Centers124[3] The Church of Jesus Christ of Latter-day Saints in the United Kingdom refers to the Church of Jesus Christ of Latter-day Saints (LDS Church) and its members in the United Kingdom. In 2019, the United Kingdom had t...

Bahasa CommunicationsspracheDibuat olehJoseph SchipferTanggal1836Pengaturan dan penggunaanBahasa pengantar internasionalTujuanBahasa buatan Bahasa pengantar internasionalCommunicationssprache SumberSebagian besar kosa kata dan tata bahasa berasal dari bahasa Prancis, dengan beberapa pengaruh dari bahasa Latin, bahasa Inggris dan bahasa JermanKode bahasaISO 639-3Tidak ada (mis)GlottologTidak adaIETFart-x-commsspr Portal BahasaSunting kotak info • L • B • PWBantu...

ErotomaniaPasien wanita yang menderita erotomania, dari karya Alexander Morison The Physiognomy of Mental DiseasesInformasi umumSpesialisasiPsikiatri Erotomania atau dikenal dengan sebutan sindroma de Clerambault adalah suatu bentuk gangguan kepribadian saat para penderitanya memiliki keyakinan bahwa orang lain memendam perasaan cinta kepada si penderita atau mungkin memiliki suatu bentuk hubungan intim.[1] Gangguan kepribadian ini rata-rata penderitanya adalah kaum Wanita.[...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Green European Foundation – news · newspapers · books · scholar · JSTOR (July 2021) (Learn how and when to remove this template message) AbbreviationGEFFormation2008TypePolitical foundation at European levelLocationRue d'Arlon 15, 1050 Brussels, BelgiumCo-Presi...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of shopping malls in Venezuela – news · newspapers · books · scholar · JSTOR (June 2014) (Learn how and when to remove this template message) This is a list of shopping malls in Venezuela.[1] Capital District Centro comercial Sambil en el municipio...

Pulau Opak Besar BaratPulau Pulau Opak Besar Barat merupakan pulau yang berada pada gugusan Kepulauan Seribu yang secara administratif termasuk dalam wilayah Kabupaten Administratif Kepulauan Seribu provinsi DKI Jakarta yang letak berdekatan dengan Pulau Air Besar, Pulau Karang Beras, Pulau Karang Congkak, Pulau Opak Besar Timur, dan Pulau Opak Kecil Lihat pula Kabupaten Administratif Kepulauan Seribu Kepulauan Seribu Pranala luar Situs resmi Kabupaten Administratif Kepulauan Seribu Diarsipka...

2012 French filmA Perfect PlanTheatrical release posterDirected byPascal ChaumeilScreenplay by Laurent Zeitoun Yoann Gromb Story byPhilippe MechelenProduced by Nicolas Duval-Adassovsky Laurent Zeitoun Yann Zenou Starring Diane Kruger Dany Boon Alice Pol CinematographyGlynn SpeeckaertEdited byDorian Rigal-AnsousMusic byKlaus BadeltProductioncompanyQuad ProductionsDistributed byUniversal PicturesRelease date 31 October 2012 (2012-10-31) (France) Running time104 minutesCountry...

Neologism This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may be unbalanced towards certain viewpoints. Please improve the article by adding information on neglected viewpoints, or discuss the issue on the talk page. (June 2012) This article possibly contains synthesis of material which does not verifiably mention or relate to the main topic. Relevant discussion may be found ...

Former horse racing venue in the Republic of Ireland This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Phoenix Park Racecourse – news · newspapers · books · scholar · JSTOR (June 2019) (Learn how and when to remove this template message) Postcard showing King Edward VII attended the races in 1904 Phoenix Park ...

جون رابي (بالألمانية: John Rabe) معلومات شخصية الميلاد 23 نوفمبر 1882[1] هامبورغ الوفاة 5 يناير 1950 (67 سنة) [1] برلين سبب الوفاة سكتة دماغية مواطنة ألمانيا أقرباء توماس رابي [لغات أخرى] (ابن الابن) الحياة العملية المهنة رائد أعمال الح�...

Para la versión SUV basada en camioneta del segmento D, véase Ford Bronco#Sexta generación (U725; 2021). Ford Bronco Sport Datos generalesOtros nombres Ford Bronco Sport (CX430)Empresa matriz Ford Motor CompanyFabricante FordProducción Hermosillo Stamping & Assembly[1]Período 2020-presenteConfiguraciónTipo Automóvil todoterrenoSegmento Segmento CPlataforma Ford C2Carrocerías SUV Crossover cinco puertasConfiguración Motor delantero transversal, tracción delantera / tracci�...

نصف السماءمعلومات عامةتاريخ الصدور 2015مدة العرض 105 دقيقةاللغة الأصلية لهجة مغربيةالبلد المغربالطاقمالمخرج عبد القادر لقطعالبطولة أنس البازصونيا عكاشةبثينة الفكاكتعديل - تعديل مصدري - تعديل ويكي بيانات نصف السماء هو فيلم مغربي من إخراج عبد القادر لقطع سنة 2015، وبطولة ك�...
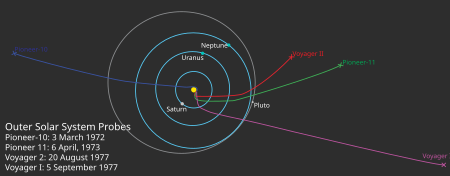
Montage Voyager 1 dan Voyager 2 saat mengunjungi planet dan bulan. Voyager 1 hanya mengobservasi Jupiter dan Saturnus sedangkan Voyager 2 mengobservasi kempat planet raksasa. Program Voyager adalah rangkaian misi luar angkasa yang diluncurkan pada tahun 1977 milik Amerika Serikat. Misi ini meliputi peluncuran dua wahana antariksa tak berawak, yaitu Voyager 1 dan Voyager 2. Keduanya diluncurkan pada tahun 1977 dengan alasan untuk memanfaatkan deretan planet yang sesuai pada akhir 1970-an. Tuju...

King of MahjongPoster filmNama lainTradisional麻雀王Sederhana麻雀王MandarinMá Què WángKantonMaa4 Zeok3 Wong4 SutradaraAdrian TehProduserAllyan TooLim TeckSkenarioLai Chaing-mingAgn Siew-hoongHo You-wangPemeranChapman ToMark LeeMichelle YeVenus WongSinematograferYong Choon-linPenyuntingKeree TehPerusahaanproduksiZingshot ProductionsRex Film ProductionLuxury Watch ClubAcross SolutionsClover FilmsAsia Tropical FilmsDistributorClover FilmsCathay-Keris Films[1]Tanggal rilis ...

هطولمعلومات عامةصنف فرعي من hydrometeor (en) جزء من طقس الأسباب سحاب ممثلة بـ كمية الأمطار تعديل - تعديل مصدري - تعديل ويكي بيانات متوسط هطول المطر حسب الشهر الهطول (جمع الهَطْل [1]) في علم الطقس: نزول الماء بكثافة على شكل مطر أو ثلج أو بَرَد[2]، أي يمكن أن يكون بشكل ماء سائل أو ...



































































