Matrix ring
|
Read other articles:

Instrument for measuring solar irradiance A pyranometer (from Greek πῦρ (pyr) 'fire', and ἄνω (ano) 'above, sky') is a type of actinometer used for measuring solar irradiance on a planar surface and it is designed to measure the solar radiation flux density (W/m2) from the hemisphere above within a wavelength range 0.3 μm to 3 μm. A typical pyranometer does not require any power to operate. However, recent technical development includes use of electronics...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. Persatuan Ulama Muslim Internasional (bahasa Arab: الإتحاد العالمي لعلماء المسلمين al-Ittihaad al-'Aalami li' Ulama'i al-Muslimin, bahasa Inggris: International Union of Muslim Scholars, disingkat IUMS) adalah sebuah Organisas...

1982 single by Whitesnake This article is about the song by Whitesnake. For other uses, see Here I Go Again (disambiguation). Here I Go AgainSingle by Whitesnakefrom the album Saints & Sinners B-sideBloody LuxuryReleasedOctober 1982[1]Recorded1982StudioGoodnight L.A. Studios, Los Angeles, USGenreGlam metalblues rock[2]Length5:09LabelGeffenSongwriter(s) David Coverdale Bernie Marsden Producer(s)Martin BirchWhitesnake singles chronology Would I Lie to You (1981) Here I Go Ag...

Town in New Hampshire, United StatesMoultonborough, New HampshireTownSwallow Boathouse in Moultonborough SealLocation in Carroll County, New HampshireCoordinates: 43°45′18″N 71°23′47″W / 43.75500°N 71.39639°W / 43.75500; -71.39639CountryUnited StatesStateNew HampshireCountyCarrollIncorporated1777VillagesMoultonboroughMoultonborough FallsLees MillSuissevaleGovernment • Board of SelectmenJonathan W. Tolman, ChairShari ColbyJean M. ...

Route in Israel Route 386כביש 386Refaim Bridge, at which the Jaffa–Jerusalem railway is passing below road 386, at the point Nahal Refaim is entering Nahal SorekRoute informationLength23 km (14 mi)Major junctionsNorth endTzur Hadassah JunctionMajor intersectionsNes Harim JunctionKerem JunctionHolland SquareMolikovsky SquareDenia SquareHaft SquareSouth endJunction at Shazar Blvd LocationCountryIsrael Highway system Roads in Israel Highways ← Route 367→ Route ...

Ираклеониты — ученики гностика Ираклеона (II век). Упоминаются как особая секта Епифанием и Августином; при крещении и миропомазании они соблюдали обряд помазания елеем и при этом произносили воззвания на арамейском языке, которые должны были освободить душу от власт�...
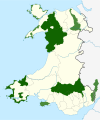
For data relating to SSSIs in this Area of Search see List of Sites of Special Scientific Interest in Conwy, Denbighshire, Flintshire, and Wrexham. Clwyd AOS SSSIs in the UK are notified using the concept of an Area of Search (AOS), an area of between 400 km2 (150 sq mi) and 4,000 km2 (1,500 sq mi) in size.[1] The Areas of Search were conceived and developed between 1975 and 1979 by the Nature Conservancy Council (NCC), based on regions creat...

Miles Teller al San Diego Comic-Con International nel 2015 Miles Alexander Teller (Downingtown, 20 febbraio 1987) è un attore statunitense. Indice 1 Biografia 2 Vita privata 3 Filmografia 3.1 Attore 3.1.1 Cinema 3.1.2 Televisione 3.1.3 Cortometraggi 3.1.4 Video musicali 3.2 Produttore 4 Premi e riconoscimenti 5 Doppiatori italiani 6 Note 7 Altri progetti 8 Collegamenti esterni Biografia Miles nasce a Downingtown, in Pennsylvania. I suoi genitori sono Merry e Mike Teller, rispettivamente un'a...

American basketball player and coach Johnny LoganLogan in 1948Personal informationBorn(1921-01-01)January 1, 1921Richmond, Indiana, U.S.DiedSeptember 16, 1977(1977-09-16) (aged 56)Charlotte, North Carolina, U.S.NationalityAmericanListed height6 ft 2 in (1.88 m)Listed weight175 lb (79 kg)Career informationHigh schoolRichmond (Richmond, Indiana)CollegeIndiana (1940–1943)Playing career1946–1951PositionGuardNumber7, 17Career historyAs player:1946–1950St. Louis ...

Національний військовий медичний центр імені Волтера Ріда Тип військовий шпитальЗасновано 1940Кількість ліжок 1200[1][2], 2464[1][2] і 244[3]Країна СШААдреса Бетесда, МерілендКоординати 39°00′07″ пн. ш. 77°05′37″ зх. д. / 39.001944444472222528° �...

Cet article est une ébauche concernant une commune de la Loire. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Le bandeau {{ébauche}} peut être enlevé et l’article évalué comme étant au stade « Bon début » quand il comporte assez de renseignements encyclopédiques concernant la commune. Si vous avez un doute, l’atelier de lecture du projet Communes de France est à votre disposition pour vous aider. Consultez également la page d’aide à...

Indian political leader and social reformer (1866–1915) Gopal Gokhale CIEGokhale in 1909Born(1866-05-09)9 May 1866Guhagar, Bombay, British RajDied19 February 1915(1915-02-19) (aged 48)Bombay, Bombay, British RajAlma materElphinstone CollegeOccupation(s)Professor, politicianPolitical partyIndian National CongressMovementIndian independence movementSpouse(s)Savitri Bai (1880–1887)Rishibama (1887–1899)Children2 Gopal Krishna Gokhale CIE (listenⓘ [ˈɡoːpaːl ˈkrɪʂɳə ˈɡo...

Soft, fine feather, sometimes under larger feathers Down feathers lack the interlocking barbules of pennaceous feathers, making them very soft and fluffy. The down of birds is a layer of fine feathers found under the tougher exterior feathers. Very young birds are clad only in down. Powder down is a specialized type of down found only in a few groups of birds. Down is a fine thermal insulator and padding, used in goods such as jackets, bedding (duvets and featherbeds), pillows and sleeping ba...

Artikel ini bukan mengenai Semut di atas kayu. Semut memanjat pohon Semut memanjat pohon Hanzi tradisional: 螞蟻上樹 Hanzi sederhana: 蚂蚁上树 Alih aksara Mandarin - Hanyu Pinyin: mǎyǐshàngshù Semut memanjat pohon (Hanzi sederhana: 蚂蚁上树; Hanzi tradisional: 螞蟻上樹; Pinyin: Mǎyǐshàngshù) adalah sebuah hidangan Sichuan klasik dalam hidangan Tionghoa.[1] Nama hidangan tersebut dalam bahasa Tionghoa, Mayishangshu, diterjemahkan menjadi semut memanj...

لوتروس Λουτρός تقسيم إداري البلد اليونان [1] المنطقة الإدارية مقدونيا الشرقية وتراقيا الوحدة الإقليمية إفروس البلدية أليكساندروبولي وحدة البلدية ترايانوبولي إحداثيات 40°52′54″N 26°02′49″E / 40.881666666667°N 26.046944444444°E / 40.881666666667; 26.046944444444 السكان التعداد السك...

مرتبة تصنيفيةمعلومات عامةصنف فرعي من تراتب اجتماعي جانب من جوانب علم التصنيف (أحياء) تعديل - تعديل مصدري - تعديل ويكي بيانات يوضح هذا الرسم البياني المراتب التصنيفية الرئيسية:النطاق، والمملكة، والشعبة، والطائفة، والرتبة، والفصيلة، والجنس، والنوع. يوضح هذا المخطط كيفية اس...

International sporting eventAthletics at the1983 Pan American GamesTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen3000 mwomen5000 mmen10,000 mmen100 m hurdleswomen110 m hurdlesmen400 m hurdlesmenwomen3000 msteeplechasemen4×100 m relaymenwomen4×400 m relaymenwomenRoad eventsMarathonmen20 km walkmen50 km walkmenField eventsHigh jumpmenwomenPole vaultmenLong jumpmenwomenTriple jumpmenShot putmenwomenDiscus throwmenwomenHammer throwmenJavelin throwmenwomenCombined...

American politician For his son, the senator, governor, and judge, see Ernest W. Gibson Jr. For his grandson, the judge, see Ernest W. Gibson III. Ernest W. GibsonUnited States Senatorfrom VermontIn officeNovember 21, 1933 – June 20, 1940Preceded byPorter H. DaleSucceeded byErnest W. Gibson Jr.Member of the U.S. House of Representativesfrom VermontIn officeNovember 6, 1923 – October 19, 1933Preceded byPorter H. DaleSucceeded byCharles A. PlumleyConstituency2n...

Dieser Artikel befasst sich mit der kanadischen Stadt. Für weitere Bedeutungen siehe Montreal (Begriffsklärung). Montréal Von oben nach unten, von links nach rechts: Skyline vom Mont Royal aus gesehen, die Altstadt (Vieux-Montréal), Notre-Dame de Montréal, der alte Hafen, St.-Josephs-Oratorium, das Olympiastadion Wappen Flagge Motto: Concordia Salus(lat.: „Wohlergehen durch Harmonie“) Lage in Québec Montréal (Québec) Montréal Staat: Kanada Kanada Provinz: Québec Région ad...

صورة لبرج جامعة بغداد الذي يضم رئاسة الجامعة وقد صممه المهندسون والتر غروبيوس وروبرت ماكميلان ولويس ماكميلن في شركة آركيتكت مولابوريتف. تنقسم جامعات العراق إلى أربع أقسام أساسية من الجامعات: الأولى هي الجامعات الحكومية؛ وهي المملوكة للحكومة، ثم جامعات إقليم كردستان؛ وهي...











