σ£¿σ╣╛Σ╜ץσ¡╕Σ╕¡∩╝לΣ║לσםבΣ╕דΘ¥óΘ½פµר»µלחµ£י27σאכΘ¥óτתהσñתΘ¥óΘ½פ∩╝לσ£¿σ»ªµץ╕τ⌐║ΘצףΣ╕¡µ▓עµ£יΣ╗╗Σ╜ץΣ║לσםבΣ╕דΘ¥óΘ½פµר»µ¡úσñתΘ¥óΘ½פ∩╝לΣ╜זσ£¿σו╢Σ╗צτ⌐║ΘצףΣ╕¡σ¡רσ£¿µ£יτפ▒27σאכσו¿τ¡יΘ¥óτ╡הµטנτתהµ¡úσñתΘ¥óΘ½פ∩╝לΣ╛כσªגσ£¿Φñחµץ╕τ⌐║ΘצףΣ╕¡∩╝לΘ╗סσí₧Σ║לσםבΣ╕דΘ¥óΘ½פµר»τפ▒27σאכσו¿τ¡יτתהΦמ½µ»פτדןµצ»∩╝םσ¥מτי╣σו½Θגךσ╜óτ╡הµטנτתהµ¡úσñתΘ¥óΘ½פ[2]πאגΘ¢צτה╢󻪵¡נσ╣╛Θחלσ╛קτ⌐║ΘצףΣ╕¡µ▓עµ£יµ¡úΣ║לσםבΣ╕דΘ¥óΘ½פ∩╝לΣ╜זΣ╗םσ¡רσ£¿Φ¿▒σñתτפ▒µ¡úσñתΘגךσ╜óτ╡הµטנτתהΣ║לσםבΣ╕דΘ¥óΘ½פ∩╝לΣ╛כσªגµ¡úΣ║פΦºעτ╜⌐σ╕│µƒ▒πאבσנלτ¢╕Σ║פΦºעσן░σíפΣ╕╕σíפσעלτץ░τ¢╕Σ║פΦºעσן░σíפΣ╕╕σíפπאגµ¡ñσñצΦªבµºכµטנΣ║לσםבΣ╕דΘ¥óΘ½פΦח│σ░סΦªבµ£י16σאכΘáגΘ╗₧[3]πאג
µ¡úΣ║לσםבΣ╕דΘ¥óΘ½פ
![]() Θ╗סσí₧Σ║לσםבΣ╕דΘ¥óΘ½פ∩╝לσו╢Σ╕¡Σ╕אσאכΘ¥óΣ╗ÑΦקםΦי▓Φí¿τñ║
Θ╗סσí₧Σ║לσםבΣ╕דΘ¥óΘ½פ∩╝לσו╢Σ╕¡Σ╕אσאכΘ¥óΣ╗ÑΦקםΦי▓Φí¿τñ║
󻪵ץ╕τ⌐║ΘצףΣ╕¡µ▓עµ£יΣ╗╗Σ╜ץτפ▒27σאכΘ¥óτ╡הµטנτתהµ¡úσñתΘ¥óΘ½פ∩╝לΣ╜זσ£¿Φñחµץ╕τ⌐║ΘצףΣ╕¡µ£יΣ╕אτ¿«τפ▒27σאכσו¿τ¡יτתהΦמ½µ»פτדןµצ»∩╝םσ¥מτי╣σו½Θגךσ╜óτ╡הµטנτתהµ¡úσñתΘ¥óΘ½פ∩╝לτג║Θ╗סσí₧Σ║לσםבΣ╕דΘ¥óΘ½פ∩╝לσו╢σ░םσב╢σñתΘ¥óΘ½פτג║µ£¼Φ║½[4]πאגτה╢Φאלσו╢Σ╜םµצ╝Φñחµץ╕τ⌐║ΘצףΣ╕¡∩╝לσ¢áµ¡ñΣ╕ªµ£¬σח║τן╛µצ╝σןñσו╕σ╣╛Σ╜ץτתהΣ║פτ¿«µ¡úσñתΘ¥óΘ½פτץ╢Σ╕¡πאג
σ╕╕ΦªכτתהΣ║לσםבΣ╕דΘ¥óΘ½פ
σ╕╕ΦªכτתהΣ║לσםבΣ╕דΘ¥óΘ½פΣ╕¡µ£יΣ╕אΣ║¢µƒ▒Θ½פΦטחΘלנΘ½פΣ╗ÑσןךΘד¿Σ╗╜τתהΦ⌐╣µú«σñתΘ¥óΘ½פσעלσםíσíפΦר¡τ½כΘ½פπאג
Σ║לσםבσו¡ΦºעΘלנ
Σ║לσםבσו¡ΦºעΘלנµר»Σ╕אτ¿«σ║ץΘ¥óτג║Σ║לσםבσו¡Θגךσ╜óτתהΘלנΘ½פ∩╝לµר»Σ║לσםבΣ╕דΘ¥óΘ½פτתהΣ╕אτ¿«∩╝לσו╢σו╖µ£י27σאכΘ¥óπאב52µó¥Θגךσעל27σאכΘáגΘ╗₧∩╝לσו╢σ░םσב╢σñתΘ¥óΘ½פµר»Φח¬σ╖▒µ£¼Φ║½[5]πאגµ¡úΣ║לσםבσו¡ΦºעΘלנµר»Σ╕אτ¿«σ║ץΘ¥óτג║µ¡úΣ║לσםבσו¡Θגךσ╜óτתהΣ║לσםבσו¡ΦºעΘלנ∩╝לσ£¿µצ╜Φנךσñ½σט⌐τ¼ªΦשƒΣ╕¡σן»Σ╗Ñτפ¿{}Γט¿{26}Σ╛זΦí¿τñ║πאגσ║ץΘגךΘץ╖τג║ πאבΘ½רτג║
πאבΘ½רτג║ τתהµ¡úΣ║לσםבσו¡ΦºעΘלנΘ½פτ⌐ם
τתהµ¡úΣ║לσםבσו¡ΦºעΘלנΘ½פτ⌐ם σעלΦí¿Θ¥óτ⌐ם
σעלΦí¿Θ¥óτ⌐ם τג║[5]∩╝ת
τג║[5]∩╝ת


Σ║לσםבΣ║פΦºעµƒ▒
Σ║לσםבΣ║פΦºעµƒ▒µר»Σ╕אτ¿«σ║ץΘ¥óτג║Σ║לσםבΣ║פΘגךσ╜óτתהµƒ▒Θ½פ∩╝לτפ▒27σאכΘ¥óπאב75µó¥Θגךσעל50σאכΘáגΘ╗₧τ╡הµטנπאגµ¡úΣ║לσםבΣ║פΦºעµƒ▒Σ╗úΦí¿µ»ןσאכΘ¥óΘד╜µר»µ¡úσñתΘגךσ╜óτתהΣ║לσםבΣ║פΦºעµƒ▒∩╝לσו╢µ»ןσאכΘáגΘ╗₧Θד╜µר»2σאכµ¡úµצ╣σ╜óσעל1σאכΣ║לσםבΣ║פΘגךσ╜óτתהσו¼σו▒ΘáגΘ╗₧∩╝לΘáגΘ╗₧σ£צΣ╗Ñ Φí¿τñ║πאגσו╢σ£¿µצ╜Φנךσñ½σט⌐τ¼ªΦשƒΣ╕¡σן»Σ╗Ñτפ¿{25}├ק{}µטצt{2,25}Σ╛זΦí¿τñ║∩╝לσ£¿Φאדσוכµצ»τי╣τ¼ªΦשƒΣ╕¡σן»Σ╗Ñτפ¿
Φí¿τñ║πאגσו╢σ£¿µצ╜Φנךσñ½σט⌐τ¼ªΦשƒΣ╕¡σן»Σ╗Ñτפ¿{25}├ק{}µטצt{2,25}Σ╛זΦí¿τñ║∩╝לσ£¿Φאדσוכµצ»τי╣τ¼ªΦשƒΣ╕¡σן»Σ╗Ñτפ¿




 Σ╛זΦí¿τñ║∩╝לσ£¿σ¿בΣ╜נσñ½τ¼ªΦשƒΣ╕¡σן»Σ╗Ñσט⌐τפ¿2 25 | 2Σ╛זΦí¿τñ║∩╝לσ£¿σ║╖σ¿בσñתΘ¥óΘ½פΦí¿τñ║µ│ץΣ╕¡σן»Σ╗Ñσט⌐τפ¿P25Σ╛זΦí¿τñ║πאגσ║ץΘגךΘץ╖τג║
Σ╛זΦí¿τñ║∩╝לσ£¿σ¿בΣ╜נσñ½τ¼ªΦשƒΣ╕¡σן»Σ╗Ñσט⌐τפ¿2 25 | 2Σ╛זΦí¿τñ║∩╝לσ£¿σ║╖σ¿בσñתΘ¥óΘ½פΦí¿τñ║µ│ץΣ╕¡σן»Σ╗Ñσט⌐τפ¿P25Σ╛זΦí¿τñ║πאגσ║ץΘגךΘץ╖τג║ πאבΘ½רτג║
πאבΘ½רτג║ τתהµ¡úΣ║לσםבΣ║פΦºעµƒ▒Θ½פτ⌐ם
τתהµ¡úΣ║לσםבΣ║פΦºעµƒ▒Θ½פτ⌐ם σעלΦí¿Θ¥óτ⌐ם
σעלΦí¿Θ¥óτ⌐ם τג║[6]∩╝ת
τג║[6]∩╝ת


Σ║פΦºעτ╜⌐σ╕│µƒ▒
Σ║פΦºעτ╜⌐σ╕│µƒ▒µר»Σ╕אτ¿«σ║ץΘ¥óτג║Σ║פΘגךσ╜óτתהτ╜⌐σ╕│µƒ▒∩╝לτפ▒27σאכΘ¥óπאב55µó¥Θגךσעל30 σאכΘáגΘ╗₧τ╡הµטנπאגµ¡úΣ║פΦºעτ╜⌐σ╕│µƒ▒µר»µלחµ»ןσאכΘ¥óΘד╜µר»µ¡úσñתΘגךσ╜óτתהΣ║פΦºעτ╜⌐σ╕│µƒ▒∩╝לσו╢µר»Σ╕אτ¿«Φ⌐╣µú«σñתΘ¥óΘ½פπאג[7]
Σ║פΦºעσן░σíפΣ╕╕σíפ
Σ║פΦºעσן░σíפΣ╕╕σíפµר»Σ╕אτ¿«τפ▒Σ║פΦºעσן░σíפΦטחΣ║פΦºעΣ╕╕σíפτ╡הσנטµטנτתהσñתΘ¥óΘ½פ∩╝לτפ▒27σאכΘ¥óπאב50µó¥Θגךσעל25σאכΘáגΘ╗₧τ╡הµטנ[8]πאגσו╢µá╣µףתτ╡הσנטµצ╣σ╝ןτתהΣ╕םσנלµ£דµ£י2τ¿«τ╡נµ₧£ΓאפΓאפσנלτ¢╕Σ║פΦºעσן░σíפΣ╕╕σíפΦטחτץ░τ¢╕Σ║פΦºעσן░σíפΣ╕╕σíפ∩╝לΘאשσו⌐τ¿«τ½כΘ½פΘד╜µר»Φ⌐╣µú«σñתΘ¥óΘ½פ[9][10]πאג
µף¼Φ⌐╣µú«σñתΘ¥óΘ½פ
Θד¿σטזµף¼Φ⌐╣µú«σñתΘ¥óΘ½פσו╖µ£י27σאכΘ¥óπאג[1]
Θד¿σטזτתהµף¼Φ⌐╣µú«σñתΘ¥óΘ½פσ¢áσו▒Θ¥óΘאאσלצτג║Σ║לσםבΣ╕דΘ¥óΘ½פ∩╝לΣ╛כσªגΣ║לσב┤Σ║פΦºעΘלנΣ║פΦºעσן░σíפΣ╕╕σíפπאג[11]
Σ║לσב┤Σ║פΦºעΘלנΣ║פΦºעσן░σíפΣ╕╕σíפ
Σ║לσב┤Σ║פΦºעΘלנΣ║פΦºעσן░σíפΣ╕╕σíפµר»µלחΣ║פΦºעσן░σíפΣ╕╕σíפτתהσו⌐σאכΣ║פΘגךσ╜óΘ¥óΦó½Σ║פΦºעΘלנσןצΣ╗úµיאσ╜óµטנτתהτ½כΘ½פ∩╝לσןטσן»Σ╗ÑσטזµטנΣ║לσב┤Σ║פΦºעΘלנσנלτ¢╕Σ║פΦºעσן░σíפΣ╕╕σíפσעלΣ║לσב┤Σ║פΦºעΘלנτץ░τ¢╕Σ║פΦºעσן░σíפΣ╕╕σíפπאגτץ╢σב┤ΘלנτתהΣ║פΦºעΘלנτג║µפ┐Σ║פΦºעΘלנµשג∩╝לΘאשσאכτ½כΘ½פσ░חµ£דσח║τן╛8τ╡הΣ╕יΦºעσ╜óσו⌐σו⌐σו▒Θ¥óτג║Φן▒σ╜ó∩╝לΘא▓ΦאלΘאאσלצτג║Σ║לσםבΣ╕דΘ¥óΘ½פπאגΘאשµ¿úτתהτ½כΘ½פσו▒τפ▒8σאכΦן▒σ╜ó∩╝טσו▒Θ¥óΘאאσלצ∩╝יπאב9σאכΣ╕יΦºעσ╜óπאב5σאכµ¡úµצ╣σ╜óσעל5σאכΣ║פΘגךσ╜óτ╡הµטנ∩╝לσו▒µ£י27σאכΘ¥óπאב52µó¥Θגךσעל27σאכΘáגΘ╗₧πאג[11]
Φ⌐╣µú«σñתΘ¥óΘ½פ
Θד¿σטזΦ⌐╣µú«σñתΘ¥óΘ½פσו╖µ£י27σאכΘ¥óπאג[12]
Σ║לσםבΣ╕דΘ¥óΘ½פσטקΦí¿
| σנםτ¿▒
|
種類
|
σ£צσדן
|
τ¼ªΦשƒ
|
ΘáגΘ╗₧
|
Θגך
|
Θ¥ó
|
╧ח
|
Θ¥óτתהτ¿«Θí₧
|
σ░םτ¿▒µאº
|
σ▒ץΘצכσ£צ
|
| Θ╗סσí₧Σ║לσםבΣ╕דΘ¥óΘ½פ
|
Φñחµ¡úσñתΘ¥óΘ½פ
|

|
3{3}3{3}3
    
|
27
|
72
|
27
|
-18
|
Φמ½µ»פτדןµצ»∩╝םσ¥מτי╣σו½Θגךσ╜ó
|
L3 = 3[3]3[3]3, 648Θתמ
|
| Σ║לσםבΣ║פΦºעµƒ▒
|
τ¿£µƒ▒Θ½פ
|
|
t{2,25}
{25}x{}
     
|
50
|
75
|
27
|
2
|
2σאכΣ║לσםבΣ║פΘגךσ╜ó
25σאכτƒ⌐σ╜ó
|
D25h, [25,2], (*25 2 2), 100Θתמ
|
|
| Σ║לσםבσו¡ΦºעΘלנ
|
τ¿£ΘלנΘ½פ
|
|
( )Γט¿{26}
|
27
|
52
|
27
|
2
|
1σאכΣ║לσםבσו¡Θגךσ╜ó
26σאכΣ╕יΦºעσ╜ó
|
C26v, [26], (*26 26)
|
|
| Σ║לσםבΣ║פΦºעΘלנσן░
|
Θלנσן░
|
|
|
50
|
75
|
27
|
2
|
2σאכΣ║לσםבΣ║פΘגךσ╜ó
25σאכµó»σ╜ó
|
C25v, [25], (*25 25)
|
|
| Θ¢שΣ╣¥ΦºעΘלנµƒ▒
|
Θ¢שΦºעΘלנµƒ▒
|
|
|
20
|
46
|
27
|
2
|
18σאכΣ╕יΦºעσ╜ó
9σאכσ¢¢Θגךσ╜ó
|
D9h, [12,2], (*2 2 9), 36Θתמ
|
|
|
|
µף¼Φ⌐╣µú«σñתΘ¥óΘ½פ[1]
|

|
|
18
|
43
|
27
|
2
|
23σאכΣ╕יΦºעσ╜ó
3σאכσ¢¢Θגךσ╜ó
1σאכΣ║פΘגךσ╜ó
|
|
|
|
|
µף¼Φ⌐╣µú«σñתΘ¥óΘ½פ[1]
|

|
|
17
|
42
|
27
|
2
|
24σאכΣ╕יΦºעσ╜ó
3σאכσ¢¢Θגךσ╜ó
|
|
|
| µ¡úΣ║פΦºעτ╜⌐σ╕│µƒ▒[7]
|
Φ⌐╣µú«σñתΘ¥óΘ½פ
|

|
|
30
|
55
|
27
|
2
|
10σאכΣ╕יΦºעσ╜ó
10σאכµ¡úµצ╣σ╜ó
6σאכΣ║פΘגךσ╜ó
1σאכσםבΘגךσ╜ó
|
C5v
|

|
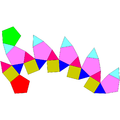
| σנלτ¢╕Σ║פΦºעσן░σíפΣ╕╕σíפ[10]
|
Φ⌐╣µú«σñתΘ¥óΘ½פ
|

|
|
25
|
50
|
27
|
2
|
15σאכΣ╕יΦºעσ╜ó
5σאכµ¡úµצ╣σ╜ó
7σאכΣ║פΘגךσ╜ó
|
C5v
|
|
| τץ░τ¢╕Σ║פΦºעσן░σíפΣ╕╕σíפ[9]
|
Φ⌐╣µú«σñתΘ¥óΘ½פ
|

|
|
25
|
50
|
27
|
2
|
15σאכΣ╕יΦºעσ╜ó
5σאכµ¡úµצ╣σ╜ó
7σאכΣ║פΘגךσ╜ó
|
C5v
|

|
| {6,3}(0,6)[13]
|
µ¡úσיחσ£░σםאσ£צ
|
|
|
54
|
81
|
27
|
0
|
σו¡Θגךσ╜ó
|
|
|
σןדΦªכ
σןדΦאדµצחτם╗
- ^ 1.0 1.1 1.2 1.3 Johnson Solid Near Misses. orchidpalms.com. [2021-08-18]. ∩╝טσמƒσºכσזוσ«╣σ¡רµíúΣ║מ2014-05-02∩╝י. ∩╝טΘí╡Θ¥óσ¡רµíúσñחΣ╗╜∩╝לσ¡רΣ║מΣ║עΦבפτ╜סµíúµíטΘªז∩╝י
- ^ Stacey, Blake C, Sporadic SICs and Exceptional Lie Algebras, sunclipse, December 30, 2018
- ^ Counting polyhedra. numericana.com. [2016-01-10]. ∩╝טσמƒσºכσזוσ«╣σ¡רµíúΣ║מ2020-08-20∩╝י. ∩╝טΘí╡Θ¥óσ¡רµíúσñחΣ╗╜∩╝לσ¡רΣ║מΣ║עΦבפτ╜סµíúµíטΘªז∩╝י
- ^ Duke, Andrew Cameron, Cube-like regular incidence complexes, Northeastern University, 2014
- ^ 5.0 5.1 Wolfram, Stephen. "Icosihexagonal pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research ∩╝טΦכ▒Φ»¡∩╝י.
- ^ Wolfram, Stephen. "Icosipentagonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research ∩╝טΦכ▒Φ»¡∩╝י.
- ^ 7.0 7.1 Weisstein, Eric W. (τ╝צ). Elongated pentagonal cupola. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. ∩╝טΦכ▒Φ»¡∩╝י.
- ^ Wolfram, Stephen. "Pentagonal orthocupolarotunda". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research. [July 24, 2010] ∩╝טΦכ▒Φ»¡∩╝י.
- ^ 9.0 9.1 Weisstein, Eric W. (τ╝צ). Pentagonal Gyrocupolarotunda. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. ∩╝טΦכ▒Φ»¡∩╝י.
- ^ 10.0 10.1 Weisstein, Eric W. (τ╝צ). Pentagonal Orthocupolarotunda. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. ∩╝טΦכ▒Φ»¡∩╝י.
- ^ 11.0 11.1 Robert R Tupelo-Schneck. Convex regular-faced polyhedra with conditional edges. tupelo-schneck.org. [2021-08-18]. ∩╝טσמƒσºכσזוσ«╣σ¡רµíúΣ║מ2021-08-18∩╝י. ∩╝טΘí╡Θ¥óσ¡רµíúσñחΣ╗╜∩╝לσ¡רΣ║מΣ║עΦבפτ╜סµíúµíטΘªז∩╝י
- ^ Gagnon, Silvain. Convex polyhedra with regular faces (PDF). Structural Topology, 1982, n├║m. 6 (Universit├⌐ du Qu├⌐bec ├á Montr├⌐al). 1982 [2021-08-18]. ∩╝טσמƒσºכσזוσ«╣σ¡רµíú (PDF)Σ║מ2017-12-12∩╝י. ∩╝טΘí╡Θ¥óσ¡רµíúσñחΣ╗╜∩╝לσ¡רΣ║מΣ║עΦבפτ╜סµíúµíטΘªז∩╝י
- ^ {6,3}(0,6). Regular Map database - map details. [2021-08-17].
|
|---|
| 1 - 10 | |
|---|
| 11 - 20 | |
|---|
| σו╢Σ╗צ | |
|---|
| µ¡úσñתΘ¥óΘ½פ | |
|---|