еңЁе№ҫдҪ•еӯёдёӯпјҢеҚҒдә”йқўй«”жҳҜжҢҮе…·жңү15еҖӢйқўзҡ„еӨҡйқўй«”гҖӮеңЁеҚҒдә”йқўй«”當дёӯжІ’жңүд»»дҪ•дёҖеҖӢеҪўзӢҖжҳҜжӯЈеӨҡйқўй«”пјҢжҸӣиЁҖд№ӢеҚіжӯЈеҚҒдә”йқўй«”дёҰдёҚеӯҳеңЁпјҢеҚҒдә”йқўй«”дәҰз„Ўжі•еЎ«е……з©әй–“пјҢжҸӣиЁҖд№ӢеҚіз©әй–“еЎ«е……еҚҒдә”йқўй«”дёҰдёҚеӯҳеңЁ[1]:88гҖӮйӣ–然жӯЈеҚҒдә”йқўй«”дёҚеӯҳеңЁпјҢдҪҶд»ҚжңүеӯҳеңЁдёҖдәӣзӯүйқўжҲ–зӯүи§’зҡ„еҚҒдә”йқўй«”пјҢдәҰжңүдёҖдәӣеҚҒдә”йқўй«”зҡҶз”ұжӯЈеӨҡйӮҠеҪўзө„жҲҗпјҢдҫӢеҰӮеҚҒдёүи§’жҹұе’Ңйӣҷдә”и§’йҢҗжҹұгҖӮ
еңЁеҢ–еӯёдёӯпјҢжңүдәӣеҺҹеӯҗз°Үе‘ҲеҚҒдә”йқўй«”[2]гҖӮиЁҲз®—иЎЁжҳҺпјҢжңүдёҖзЁ®еҚҒдә”йқўй«”зҡ„жҷ¶иғһеңЁжҷ¶й«”дёӯжҳҜз©©е®ҡзҡ„[3]гҖӮ
жӯӨеӨ–пјҢжңүдёҖзЁ®еёізҜ·зҡ„зөҗж§ӢжҳҜиЁӯиЁҲзӮәзӯүеҚҒдә”йқўй«”гҖӮ[4]然иҖҢйҖҷеҖӢеҚҒдә”йқўй«”дёҚеҢ…еҗ«еә•йқўпјҢиӢҘиЁҲе…Ҙеә•йқўпјҢи©Із«Ӣй«”жҮүзӮәеҚҒе…ӯйқўй«”гҖӮ
еҮёеҚҒдә”йқўй«”
жүҖжңүеҚҒдә”йқўй«”дёӯдёҖе…ұжңү23,833,988,129еҖӢжӢ“ж’ІдёҚеҗҢж§Ӣзҡ„еҮёеҚҒдә”йқўй«”пјҢдёҚеҢ…жӢ¬йҸЎеғҸпјҢдёҰдё”иҮіе°‘йңҖиҰҒеҢ…еҗ«10еҖӢй Ӯй»һ[5]пјҲеҰӮжһңе…©еҖӢеӨҡйқўй«”е…·жңүжң¬иіӘдёҠдёҚеҗҢзҡ„йқўжҺ’еҲ—гҖҒйӮҠиҲҮй Ӯй»һзҡ„зӣёжҺҘж–№ејҸпјҢеүҮе®ғеҖ‘жҳҜвҖңжӢ“ж’ІдёҚеҗҢж§ӢвҖқпјҢеӣ зӮәеҰӮжһңе…©еҖӢз«Ӣй«”й–“жңүдёҚеҗҢзҡ„йқўжҺ’еҲ—гҖҒйӮҠиҲҮй Ӯй»һзҡ„зӣёжҺҘж–№ејҸпјҢеүҮе°ұз„Ўжі•еғ…йҖҸйҒҺж”№и®ҠйӮҠзҡ„й•·еәҰжҲ–йӮҠжҲ–йқўд№Ӣй–“зҡ„и§’еәҰдҫҶе°ҮдёҖеҖӢеӨҡйқўй«”еҪўи®ҠжҲҗеҸҰдёҖеҖӢпјүгҖӮ
еёёиҰӢзҡ„еҚҒдә”йқўй«”
еҚҒдёүи§’жҹұ
![]() жӯЈеҚҒдёүи§’жҹұ
жӯЈеҚҒдёүи§’жҹұ
еҚҒдёүи§’жҹұжҳҜдёҖзЁ®еә•йқўзӮәеҚҒдёүйӮҠеҪўзҡ„жҹұй«”пјҢжҳҜеҚҒдә”йқўй«”зҡ„дёҖзЁ®пјҢе…¶з”ұ15еҖӢйқўгҖҒ26еҖӢй Ӯй»һе’Ң39еҖӢйӮҠзө„жҲҗгҖӮжӯЈеҚҒдёүи§’жҹұд»ЈиЎЁжҜҸеҖӢйқўйғҪжҳҜжӯЈеӨҡйӮҠеҪўзҡ„еҚҒдёүи§’жҹұпјҢе…¶жҜҸеҖӢй Ӯй»һйғҪжҳҜ2еҖӢжӯЈж–№еҪўе’Ң1еҖӢеҚҒдёүйӮҠеҪўзҡ„е…¬е…ұй Ӯй»һпјҢй Ӯй»һең–д»Ҙ иЎЁзӨәпјҢеңЁж–ҪиҗҠеӨ«еҲ©з¬ҰиҷҹдёӯеҸҜд»ҘеҲ©з”Ё{13}Г—{} жҲ– t{2, 13}дҫҶиЎЁзӨәпјӣеңЁиҖғе…Ӣж–Ҝзү№вҖ”иҝӘиӮҜз¬ҰеҸ·дёӯеҸҜд»ҘеҲ©з”Ё
иЎЁзӨәпјҢеңЁж–ҪиҗҠеӨ«еҲ©з¬ҰиҷҹдёӯеҸҜд»ҘеҲ©з”Ё{13}Г—{} жҲ– t{2, 13}дҫҶиЎЁзӨәпјӣеңЁиҖғе…Ӣж–Ҝзү№вҖ”иҝӘиӮҜз¬ҰеҸ·дёӯеҸҜд»ҘеҲ©з”Ё
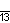


 дҫҶиЎЁзӨәпјӣеңЁеЁҒдҪҗеӨ«з¬ҰиҷҹдёӯеҸҜд»ҘеҲ©з”Ё2 13 | 2дҫҶиЎЁзӨәпјӣеңЁеә·еЁҒеӨҡйқўй«”иЎЁзӨәжі•дёӯеҸҜд»ҘеҲ©з”ЁP13дҫҶиЎЁзӨәгҖӮиӢҘдёҖеҖӢжӯЈеҚҒдёүи§’жҹұеә•йӮҠзҡ„йӮҠй•·зӮә
дҫҶиЎЁзӨәпјӣеңЁеЁҒдҪҗеӨ«з¬ҰиҷҹдёӯеҸҜд»ҘеҲ©з”Ё2 13 | 2дҫҶиЎЁзӨәпјӣеңЁеә·еЁҒеӨҡйқўй«”иЎЁзӨәжі•дёӯеҸҜд»ҘеҲ©з”ЁP13дҫҶиЎЁзӨәгҖӮиӢҘдёҖеҖӢжӯЈеҚҒдёүи§’жҹұеә•йӮҠзҡ„йӮҠй•·зӮә гҖҒй«ҳзӮә
гҖҒй«ҳзӮә пјҢеүҮе…¶й«”з©Қ
пјҢеүҮе…¶й«”з©Қ е’ҢиЎЁйқўз©Қ
е’ҢиЎЁйқўз©Қ зӮә[6]пјҡ
зӮә[6]пјҡ


еҚҒеӣӣи§’йҢҗ
 еҚҒеӣӣи§’йҢҗ
еҚҒеӣӣи§’йҢҗ
еҚҒеӣӣи§’йҢҗжҳҜдёҖзЁ®еә•йқўзӮәеҚҒеӣӣйӮҠеҪўзҡ„йҢҗй«”пјҢжҳҜеҚҒдә”йқўй«”зҡ„дёҖзЁ®пјҢе…¶е…·жңү15еҖӢйқўгҖҒ28жўқйӮҠе’Ң15еҖӢй Ӯй»һпјҢе…¶е°ҚеҒ¶еӨҡйқўй«”жҳҜиҮӘе·ұжң¬иә«[7]гҖӮжӯЈеҚҒеӣӣи§’йҢҗжҳҜдёҖзЁ®еә•йқўзӮәжӯЈеҚҒеӣӣйӮҠеҪўзҡ„еҚҒеӣӣи§’йҢҗгҖӮиӢҘдёҖеҖӢжӯЈеҚҒеӣӣи§’йҢҗеә•йӮҠзҡ„йӮҠй•·зӮә гҖҒй«ҳзӮә
гҖҒй«ҳзӮә пјҢеүҮе…¶й«”з©Қ
пјҢеүҮе…¶й«”з©Қ е’ҢиЎЁйқўз©Қ
е’ҢиЎЁйқўз©Қ зӮә[7]пјҡ
зӮә[7]пјҡ


и©№жЈ®еӨҡйқўй«”
еңЁи©№жЈ®еӨҡйқўй«”дёӯеҸӘжңүдёҖзЁ®е…·жңүеҚҒдә”еҖӢйқў[8]пјҢе…¶зӮәйӣҷдә”и§’йҢҗжҹұгҖӮ
и©№жЈ®еӨҡйқўй«”е°ҚеҒ¶
йғЁеҲҶи©№жЈ®еӨҡйқўй«”е…·жңү15еҖӢй Ӯй»һ[9]пјҢеӣ жӯӨе…¶е°ҚеҒ¶еӨҡйқўй«”зӮәеҚҒдә”йқўй«”пјҢйҖҷдәӣз«Ӣй«”жңүжӯЈдә”и§’еёіеЎ”зҡ„е°ҚеҒ¶гҖҒжӯЈдёүи§’еёіеЎ”жҹұзҡ„е°ҚеҒ¶гҖҒдёүеҒҙйҢҗе…ӯи§’жҹұзҡ„е°ҚеҒ¶гҖҒеҒҙеёіеЎ”жҲӘи§’еӣӣйқўй«”зҡ„е°ҚеҒ¶зӯүеӨҡйқўй«”гҖӮ
еҚҒдә”йқўй«”еҲ—иЎЁ
| еҗҚзЁұ
|
зЁ®йЎһ
|
ең–еғҸ
|
з¬Ұиҷҹ
|
й Ӯй»һ
|
йӮҠ
|
йқў
|
ПҮ
|
йқўзҡ„зЁ®йЎһ
|
е°ҚзЁұжҖ§
|
еұ•й–Ӣең–
|
| еҚҒдёүи§’жҹұ
|
зЁңжҹұй«”
|

|
t{2,13}
{13}x{}
     
|
26
|
39
|
15
|
2
|
2еҖӢеҚҒдёүйӮҠеҪў
13еҖӢзҹ©еҪў
|
D13h, [13,2], (*13 2 2)
|
| еҚҒеӣӣи§’йҢҗ
|
зЁңйҢҗй«”
|

|
( )вҲЁ{14}
|
15
|
28
|
15
|
2
|
1еҖӢеҚҒеӣӣйӮҠеҪў
14еҖӢдёүи§’еҪў
|
C14v, [14], (*14 14)
|
|
| дёғи§’йҢҗжҹұ
|
и§’йҢҗжҹұ
|

|
|
15
|
28
|
15
|
2
|
7еҖӢдёүи§’еҪў
7еҖӢзҹ©еҪў
1еҖӢдёғйӮҠеҪў
|
D7h, [7,2], (*227), order 28
|
|
| дёғи§’йҢҗеҸ°йҢҗ
|
жҲӘи§’йӣҷйҢҗ
|

|
|
15
|
28
|
15
|
2
|
7еҖӢдёүи§’еҪў
7еҖӢжўҜеҪў
1еҖӢдёғйӮҠеҪў
|
D7h, [7,2], (*227), order 28
|
|
| йӣҷдә”и§’йҢҗжҹұ
|
йӣҷи§’йҢҗжҹұ
и©№жЈ®еӨҡйқўй«”
|

|
|
12
|
25
|
15
|
2
|
10еҖӢдёүи§’еҪў
5еҖӢжӯЈж–№еҪў
|
D5h, [5,2], (*225)
|

|
| жӯЈдә”и§’еёіеЎ”зҡ„е°ҚеҒ¶
|
и©№жЈ®еӨҡйқўй«”зҡ„е°ҚеҒ¶
|

|
|
12
|
25
|
15
|
2
|
10еҖӢдёүи§’еҪў
5еҖӢй·ӮеҪў
|
D5h, [5,2], (*225)
|

|
| дёүи§’еёіеЎ”жҹұзҡ„е°ҚеҒ¶
|
и©№жЈ®еӨҡйқўй«”зҡ„е°ҚеҒ¶
|

|
|
14
|
27
|
15
|
2
|
6еҖӢзӯүи…°дёүи§’еҪў
9еҖӢеӣӣйӮҠеҪў
|
C3v
|

|
| жӯЈдёүи§’еёіеЎ”еҸҚи§’жҹұзҡ„е°ҚеҒ¶
|
и©№жЈ®еӨҡйқўй«”зҡ„е°ҚеҒ¶
|

|
|
16
|
33
|
15
|
2
|
6еҖӢдә”йӮҠеҪў
3еҖӢеӣӣйӮҠеҪў
6еҖӢй·ӮеҪў
|
C3v
|

|
еҸӮиҖғиө„ж–ҷ
- ^ её•е…ӢйәҘзү№. ж•ёеӯёеӨ§и§Җеҝө2пјҡеҫһжҺҗжҢҮдёҖз®—еҲ°з©ҝи¶Ҡеӣӣж¬Ўе…ғзҡ„ж•ёеӯёйӯ”иЎ“. иІ“й ӯй·№жӣёжҲҝ. Mao tou ying chu ban. 2020 [2022-08-28]. ISBN 9789862624265. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2022-08-28пјү.
- ^ Montejano, JM and RodrГӯguez, JL and Gutierrez-Wing, C and Miki, M and JosГ©-YacamГЎn, M. Crystallography and Shape of Nanoparticles and Clusters (PDF). Encyclopedia of Nanoscience and Nanotechnology X. 2004: 1вҖ“44 [2022-08-28]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ (PDF)дәҺ2022-08-28пјү.
- ^ Lagunov, VA and Sinani, AB. Formation of a bistructure of a solid in a computer experiment. Physics of the Solid State (Springer). 1998, 40 (10): 1742вҖ“1747 [2022-08-28]. doi:10.1134/1.1130648. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2022-08-28пјү.
- ^ CN patent 201280830Y,еҚ“ж–° & еҗҙе»әжҢә,гҖҢзӯүеҚҒдә”йқўдҪ“еёҗзҜ·з»“жһ„гҖҚ,еҸ‘иЎЁдәҺ2009-07-29,жҢҮе®ҡдәҺжөҷжұҹеӨ§еӯҰе’Ңжөҷжұҹеұ•иҜҡе»әи®ҫйӣҶеӣўиӮЎд»Ҫжңүйҷҗе…¬еҸё
- ^ Counting polyhedra. numericana.com. [2022-08-28]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2016-05-06пјү.
- ^ Wolfram, Stephen. "Tridecagonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research пјҲиӢұиҜӯпјү.
- ^ 7.0 7.1 Wolfram, Stephen. "Tetradecagon pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research пјҲиӢұиҜӯпјү.
- ^ Johnson, Norman W. Convex Solids with Regular Faces. Canadian Journal of Mathematics. 1966, 18: 169вҖ“200. ISSN 0008-414X. Zbl 0132.14603. doi:10.4153/cjm-1966-021-8.
- ^ Gagnon, Sylvain. Les polyГЁdres convexes aux faces rГ©guliГЁres [Convex polyhedra with regular faces] (PDF). Structural Topology. 1982, (6): 83вҖ“95 [2022-08-28]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ (PDF)дәҺ2017-12-12пјү.
|
|---|
| 1 - 10 | |
|---|
| 11 - 20 | |
|---|
| е…¶д»– | |
|---|
| жӯЈеӨҡйқўй«” | |
|---|