|
ä¸é˘éŤ
ĺ¨ĺšžä˝ĺ¸ä¸ďźä¸é˘éŤćŻćçą7ĺé˘çľćçĺ¤é˘éŤăć˛ćäťťä˝ä¸ç¨Žä¸é˘éŤćŻćŁä¸é˘éŤďźäšĺ°ąćŻčŞŞćžä¸ĺ°ććé˘ĺ
¨çăććéçéˇăććč§ç¸ççä¸é˘éŤďźćä¸ç¨ŽçéçĺŽćŁçä¸é˘éŤďźçąĺĺä¸č§ĺ˝˘ĺä¸ĺĺé形çľćďźĺ
śčçž
錏ć˛é˘ć樸ĺć§[1][2] ăć¤ĺ¤äşŚĺćçéĺçč§çä¸é˘éŤďźĺłäşč§ćąďźććć稹çşĺćŁä¸é˘éŤďźä˝ä¸ćĺ°ĺŽçä˝ćŻéżĺşçąłĺžˇçŤéŤ[3]ă
常čŚçä¸é˘éŤ
常čŚçä¸é˘éŤćĺ
č§éăäşč§ćąăćŁä¸č§éćąăĺ¸ć´čĽżä¸é˘éŤäťĽĺä¸äşĺŞéçĺ
Ťé˘éŤ[4]çĺ¤é˘éŤă
ĺ¨ććä¸é˘éŤä¸ďźĺŞććŁä¸č§éćąćŻčŠšćŁŽĺ¤é˘éŤă
äşč§ćą
äşč§ćąćŻä¸ç¨Žĺşé˘çşäşé形çćąéŤďźçą7ĺé˘15ć˘éĺ10ĺé éťçľćăćŁäşč§ćąäťŁčĄ¨ćŻĺé˘é˝ćŻćŁĺ¤é形çäşč§ćąďźĺ
śćŻĺé éťé˝ćŻ2ĺćŁćšĺ˝˘ĺ1ĺäşé形çĺ
Źĺ
ąé éťďźĺ ć¤ĺ
ˇććŻĺč§çč§çć§čłŞďźĺŻäťĽć¸éĄçşĺćŁä¸é˘éŤă
ĺ
č§é
ĺ
č§éćŻä¸ç¨Žĺşé˘çşĺ
é形çééŤďźĺ
śĺ
ˇć7ĺé˘ă14ć˘éĺ7ĺé éťďźĺ
śĺ°ĺśĺ¤é˘éŤćŻčŞĺˇąćŹčşŤăćŁĺ
č§éćŻä¸ç¨Žĺşé˘çşćŁĺ
é形çĺ
č§éă
ä¸é˘éŤĺ襨
| ĺ稹
|
税éĄ
|
ĺĺ
|
珌č
|
é éť
|
é
|
é˘
|
Ď
|
é˘ç税éĄ
|
ĺ°ç¨ąć§
|
ĺąéĺ
|
| ĺ
č§é
|
ééŤ
|
![]()
|
( )â¨{6}
|
7
|
12
|
7
|
2
|
1ĺĺ
é形
6ĺä¸č§ĺ˝˘
|
C6v, [6], (*66)
|
| äşč§ćą
|
ćąéŤ
|

|
t{2,5}
{5}x{}
    
|
10
|
15
|
7
|
2
|
2ĺäşé形
5ĺçŠĺ˝˘
|
D5h, [5,2], (*522), order 20
|

|
| ä¸č§éćą
|
č§éćą
芚棎ĺ¤é˘éŤ
|

|
P3+Y3
|
7
|
12
|
7
|
2
|
4ĺä¸č§ĺ˝˘
3ĺćŁćšĺ˝˘
|
C3v, [3], (*33)
|

|
| ä¸č§éĺ°é
|
ćŞč§éé
|

|
|
7
|
12
|
7
|
2
|
4ĺä¸č§ĺ˝˘
3ĺ梯形
|
C3v, [3], (*33)
|

|
| ĺé˘ĺĺ
é˘éŤ
|
ć形ĺ¤é˘éŤ
|

|
3/2 3 | 2
|
6
|
12
|
7
|
1
|
4ĺä¸č§ĺ˝˘ 
3ĺćŁćšĺ˝˘
|
Td, [4,3], *432
Td, [3,3], *332
|
| 輿ć´ĺ¸ä¸é˘éŤ
|
ç°ĺ˝˘ĺ¤é˘éŤ
|
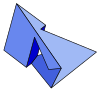
|
|
14[5]
|
21[5]
|
7[5]
|
1
|
3ĺ°ĺšĺ
é形   
1ĺĺšłčĄĺ
é形 
|
C1, [ ]+, (11)
|

|
éĺ¸ä¸é˘éŤ
ć樸ĺ¸ä¸çä¸é˘éŤ
ĺ
ąć34税ć樸çľć§ć饯塎ç°çĺ¸ä¸é˘éŤ[6]ă
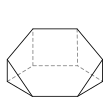
- é˘ççľćďź6,6,4,4,4,3,3
- 10ĺé éť
- 15ć˘é
|

- é˘ççľćďź6,5,5,5,3,3,3
- 10ĺé éť
- 15ć˘é
|

- é˘ççľćďź6,5,5,4,4,3,3
- 10ĺé éť
- 15ć˘é
|
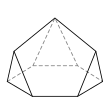
- é˘ççľćďź6,5,4,4,3,3,3
- 9ĺé éť
- 14ć˘é
|
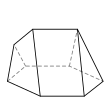
- é˘ççľćďź6,5,4,4,3,3,3
- 9ĺé éť
- 14ć˘é
|
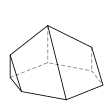
- é˘ççľćďź6,4,4,4,4,3,3
- 9ĺé éť
- 14ć˘é
|

- é˘ççľćďź6,4,4,3,3,3,3
- 8ĺé éť
- 13ć˘é
|

- é˘ççľćďź6,4,4,3,3,3,3
- 8ĺé éť
- 13ć˘é
|

ĺ
č§é
- é˘ççľćďź6,3,3,3,3,3,3
- 7ĺé éť
- 12ć˘é
|

- é˘ççľćďź5,5,5,4,4,4,3
- 10ĺé éť
- 15ć˘é
|
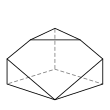
- é˘ççľćďź5,5,5,4,3,3,3
- 9ĺé éť
- 14ć˘é
|
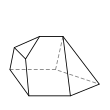
- é˘ççľćďź5,5,5,4,3,3,3
- 9ĺé éť
- 14ć˘é
|
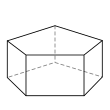
äşč§ćą
- é˘ççľćďź5,5,4,4,4,4,4
- 10ĺé éť
- 15ć˘é
|
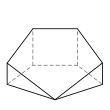
- é˘ççľćďź5,5,4,4,4,3,3
- 9ĺé éť
- 14ć˘é
|

- é˘ççľćďź5,5,4,4,4,3,3
- 9ĺé éť
- 14ć˘é
|
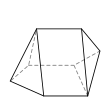
- é˘ççľćďź5,5,4,3,3,3,3
- 8ĺé éť
- 13ć˘é
|
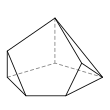
- é˘ççľćďź5,5,4,3,3,3,3
- 8ĺé éť
- 13ć˘é
|
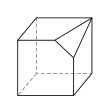
- é˘ççľćďź5,4,4,4,4,4,3
- 9ĺé éť
- 14ć˘é
|

- é˘ççľćďź5,4,4,4,3,3,3
- 8ĺé éť
- 13ć˘é
|
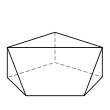
- é˘ççľćďź5,4,4,4,3,3,3
- 8ĺé éť
- 13ć˘é
|
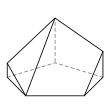
- é˘ççľćďź5,4,4,4,3,3,3
- 8ĺé éť
- 13ć˘é
|
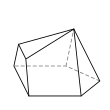
- é˘ççľćďź5,4,4,4,3,3,3
- 8ĺé éť
- 13ć˘é
|

- é˘ççľćďź5,4,4,4,3,3,3
- 8ĺé éť
- 13ć˘é
|
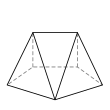
- é˘ççľćďź5,4,3,3,3,3,3
- 7ĺé éť
- 12ć˘é
|

- é˘ççľćďź5,4,3,3,3,3,3
- 7ĺé éť
- 12ć˘é
|
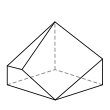
- é˘ççľćďź4,4,4,4,4,3,3
- 8ĺé éť
- 13ć˘é
|

- é˘ççľćďź4,4,4,4,4,3,3
- 8ĺé éť
- 13ć˘é
|

ä¸č§éćą
- é˘ççľćďź4,4,4,3,3,3,3
- 7ĺé éť
- 12ć˘é
|
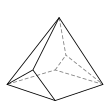
- é˘ççľćďź4,4,4,3,3,3,3
- 7ĺé éť
- 12ć˘é
|

- é˘ççľćďź4,4,4,3,3,3,3
- 7ĺé éť
- 12ć˘é
|

- é˘ççľćďź4,4,4,3,3,3,3
- 7ĺé éť
- 12ć˘é
|
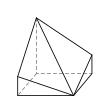
- é˘ççľćďź4,4,4,3,3,3,3
- 7ĺé éť
- 12ć˘é
|

- é˘ççľćďź4,3,3,3,3,3,3
- 6ĺé éť
- 11ć˘é
|
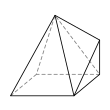
- é˘ççľćďź4,3,3,3,3,3,3
- 6ĺé éť
- 11ć˘é
|
ĺčćçť
- ^ Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. New York: Viking Penguin, p. 98, 1991. ISBN 978-0140118131
- ^ Dharwadker, A. "Heptahedron and Roman Surface." ďźéĄľé˘ĺ楣ĺ¤äť˝ďźĺäşäşčç˝ćĄŁćĄéŚďź Electronic Geometry Model No. 2003.05.001.
- ^ Weisstein, Eric W. (çź). Heptahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. ďźčąčŻďź.
- ^ Holden, A. Shapes, Space, and Symmetry. New York: Dover, p. 95, 1991. ISBN 978-0486268514
- ^ 5.0 5.1 5.2 Ace, Tom, The Szilassi polyhedron, [2016-08-14], ďźĺĺ§ĺ
厚ĺ楣äş2016-09-07ďź
- ^ Counting polyhedra. numericana.com. [2016-1-10]. ďźĺĺ§ĺ
厚ĺ楣äş2016-05-06ďź.
ĺ¤é¨éŁçľ
|
|---|
| 1 - 10 | |
|---|
| 11 - 20 | |
|---|
| ĺ
śäť | |
|---|
| ćŁĺ¤é˘éŤ | |
|---|
|
|