![]() ̓ÒÀÍÛ¿Ì¿
̓ÒÀÍÛ¿Ì¿
 ̓ÒÀÍÛ¿Ì¿Í ð§ÒÏÈ
̓ÒÀÍÛ¿Ì¿Í ð§ÒÏÈ
 ÌÇÕ ÐÍËÒÀÍۿ̿̓Ð
ÌÇÕ ÐÍËÒÀÍۿ̿̓Ð
̓ÒÀÍÛ¿Ì¿Ì₤ÍÊð£Èð¡Ù̯ͧÍÙÎð¡ÙÓð¡ð¡ˆÍ§ÕÂÐͤ҈Ðð¿Ó¨ ÓÛÌ₤ÐÓ˜˜ð¿ÍñÐ̓ÒÀÐÓ¨ Ó˜˜Íð¤ÕÂÐÓ£ð¡Í§ÌÑ̯ÍÙÎÍÛÑÍ̓§ÒÛ¤Ò₤ÿ¥Í
ÑÍÍÓ£ð¡ÙͧÍð£È̯ÍÙÎÍÛÑÓ ÓˋÑÍÌˋÍ
ð¡¤ÒÀð¡ÙÍÛ¿ÓÇÿ¥Íƒð¡ÙÍÛ¿Ì´ˆÿ¥ÓÝÌÙÊð¤ÏÓð¡ÍËÍ
ñÌð¡Ùͧð¥ ӣ̯ÍÙÎÓ¿ÒýÓÌÝÒÏÈÓÇÒÏð¡ÒÏͧÂÍ ð§ÍÙÎÕÛÕÂÓÌ¿Ì°ÿ¥Í¿¢Ì°Ó´ð¤Í´ð¡ÙͧÍÊð£ÈÍ ð§ÍÙÎÍÌçÕÍÙÎÐð¡ÙͧÍÊð£ÈÌýÀÌÍÊÍ¡Ò
̘ÏÍ ÕÍƒÍ ð§ÍÙÎÓÍ¿°ÒÀÓ¤¢ÌÎÍ¢çÿ¥ÕÓ´ÍÛ¿Ì¿ÐÍÛ¿Ì´ˆÐÍÛ¿ÓÇÌÎÍ¢çÿ¥ÌÑͯͥÌýÍÍñËÓÌÓ´Ð
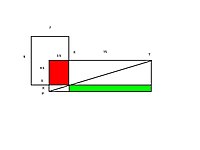
Ðð¿Ó¨ ÓÛÌ₤ÐÓ˜˜ð¿ÍñÐ̓ÒÀÐÓ¨ Ó˜˜Íð¤ÕÂÿ¥ãð£Ì̓ð¤ÌÙËÿ¥ÒÀÍð¤ÌÙËÿ¥ÕÛ̓ð¡ÙÍÛ¿Ì¿Í ð§ÿ¥ÓÙ̯ð¡ÌÙËÍð¡ÍÌÙËð¿ð¿ÐÌ₤̯ÿ¥Í¿Ñ̓ÒÀð¡¤Ì°ÿ¥ÍƒÒÀÓ¡ð¿ð¡¤ÍÛÿ¥ÍÛÍÎÌ°Òð¡ÿ¥ÍƒÌ¿ð¡ÌÙËÐãÍÎ̓ÓÇÒÏð¡ÒÏͧÂABCð¡ÙÍ
ÌËÌÙÈ̿ͧÂDEFBÐÓÇÒÏð¡ÒÏͧÂÕ¨ÿ¥ÒÀÿ¥ÿ¥H=ABÿ¥Í¤Õ¢ÿ¥Íƒÿ¥L=BCÿ¥ÌÙÈ̿ͧÂÒƒ¿Õ¢ð¡¤XÐÓÙÌÀÿ¥ð£Ë̓5ÌÙËÐÒÀ12ÌÙËð¿Íð¡¤ÍÌ₤ÿ¥Í¿Ñ̓ÒÀð¡¤Ì°ÿ¥ÿ¥ð£Ë̓5ÌÙËÐÒÀ12ÌÙËð¿ÓÏ₤ð¡¤ÍÍÙÿ¥ÍƒÒÀÓ¡ð¿ð¡¤ÍÛÿ¥ÿ¥ÍƒÍƒð¡ÙÍÛ¿Ì¿ð¿Òƒ¿Õ¢= 12x5/(12+5) = 60/17 = 3Ð9/17
Í̓§ð¡¤ÍƒÒÀÍÛ¿Ì¿ÓÍ
°Ó°£Í¥ÿ¥Ìðƒð¤ð¡Êð¡ˆÒ₤Ìÿ¥ð¡ð¡ˆÌ₤ÍˋӴͤÍ
ËÓ¡ÒÀËÍÓÿ¥Í°ÍˋÓ´Í ð§ÍƒÍ§ÂÍ´ÓϣʹÐÒ§˜Í´ÌÑÕÂÓÏ₤ÍÛÌÿ¥Í¯Í ð§ÍƒÍ§ÂÕ̯ÌÍÿ¥ð£ËÌÝÓ£ÌÓÌ¿Ì°ÐÍ
ͯð¡ÒÏͧÂABCÍÊÍÑÿ¥ÍÓ§Ûÿ¥ÍÍð¡ÒÏͧÂÍð§çÌð¡¤ð¡ð¡ˆÕ¨ð¡¤HÐÍÛ§ð¡¤LÓբ̿ͧÂÿ¥ÍÎ̓Ðͯð¡Êð¡ˆÕÕñÓ¤XÓÌÙÈ̿ͧÂÌ ð£ËÕ£Òýÿ¥ð¡Êð¡ˆÍÊÏÓÇÒÏð¡ÒÏͧÂÌ ð£ËÓ¤ÂÒýÿ¥ð¡Êð¡ˆÍ¯ÓÇÒÏð¡ÒÏͧÂÌ ð£ËÕÒý[1]ÐÍͯÍñÎ̓Óð¡Êð¡ˆÕ£ÒýÌÙÈ̿ͧÂÐð¡Êð¡ˆÓ¤ÂÒýÍÊÏÓÇÒÏð¡ÒÏͧÂÐð¡Êð¡ˆÕÒýͯÓÇÒÏð¡ÒÏͧÂÿ¥Õ̯ÌÍÍÎͰ̓Ðð£Í¤Í
ËÓ¡ÒÀËÿ¥ÕÂÓÏ₤ÍÛÌÍÓÿ¥ÍñÎ̓ÓÕÂÓÏ₤ÍͰ̓ÓÕÂÓÏ₤Ó¡ÓÙÐÍñÎ̓ÕÂÓÏ₤=HLÿ¥ Ͱ̓ÕÂÓÏ₤=X(H+L)[2]
HL = X(H+L)
ÓÝÌÙÊ̓ͤ̓ÒÀÍÛ¿Ì¿ÓÍ
°Ó°£Í¥ÿ¥
ÕÕ¢ X = HL / (H+L)
Í̓§ÓÓ˜˜ð¤ð¡ˆÒ₤Ìÿ¥ÍˋÓ´Ó¡ð¥¥ð¡ÒÏͧÂÌ₤Óð¡ÍÍÓÐÍ̓§Ì°´Ì¯ÿ¥ãͿ̓̿ʹ̓ð¡Ùÿ¥ÍÌ¿ð¿ð¡ÊÍ£ÍÒˆÌͯ̓ÒÀÿ¥Í
ÑÓ¡ð¡ð¿Í¢ÿ¥ð¡ÍÊÝ̘Óð¿ãÐ
Í°Í
ÌËÌÙÈ̿ͧÂDEFBÓð¡ÊÒƒ¿DE,EFð¡ÓÇÒÏð¡ÒÏͧÂÓð¡Òƒ¿ÿ¥Í҈ͧÂÌͯÓÓÇÒÏð¡ÒÏͧÂÿ¥ÒÒ¢ð¡Êð¡ˆÍ¯ÓÇÒÏð¡ÒÏͧÂð¡Òƒ¿ÓÌ₤Óÿ¥ÍÍÌËÍÊÏÓÇÒÏð¡ÒÏͧÂÓð¡Òƒ¿Ì₤ÓÓ¡ÍÐÍ̓§ð£Íƒð¡ÙÍÛ¿Ì¿ð¡ÙͧӤ°Í¤ãð¡ÍÊÝ̘ÓãÍÓÿ¥Í°ð¡ð¡ˆÓ¡ð¥¥ð¡ÒÏͧÂÌ₤ÓÓ¡ÍÐ
- AD : DE : AE = EF : FC : EC = AB : BC : AC
ð£ÊÒÀÕ¨ð¡¤Hÿ¥ÍƒÕ¢ð¡¤Lÿ¥ÍƒÒÀÍÛ¿Ì¿ÓÒƒ¿Õ¢ð¡¤Xÿ¥Ì ¿ÌÛð¡ÍÊÝ̘ÓÍÓÿ¥
- (H-X) : X = H : L
- HL - XL = HX
- HX + XL = HL
- ̓̓ÒÀÍÛ¿Ì¿Í
°Ó°£Í¥ÐÐÐÿ¥¡ÿ¥ÿ¥´ÿ¥˜ÿ¥ÿ¥ÿ¥´ÿ¥ÿ¥˜ÿ¥
ÒÀð¡ÙÍÛ¿ÓÇ
 ̓ð¡ÙÍÛ¿Ì¿ ÒÀð¡ÙÍÛ¿ÓÇ
̓ð¡ÙÍÛ¿Ì¿ ÒÀð¡ÙÍÛ¿ÓÇ
̓ð¡ÙÍÛ¿Ì¿Í₤ð£ËÒ§˜Íð¡¤ÒÀð¡ÙÍÛ¿ÓÇ
ͯð¡ÒÏͧÂABCÍÓ§Ûÿ¥ð¡ð¿ÕÍ Ìբ̿ͧÂABCD ÍÎ̓ÿ¥Í
Ñ̘Àð£Íƒð¡ÙÍÛ¿Ì¿ÌËÒÏÎÓ¿Eӣ̯ÇÍ¿°Ó¤¢EMÿ¥ÍÓÇÓ¤¢EKÿ¥ð¡Õ¢Ì¿Í§ÂÓÒƒ¿Ó¡ð¤Êÿ¥ÍÎ̓ÿ¥ð¡ÒÏͧÂACDÍ
ÌËբ̿ͧÂKDMEÿ¥ÌÌÒÀð¡ÙÍÛ¿ÓÇÐ
̓ð¡Ùð¡ÒÏͧÂABCð¡ÙÍ
ÌËÓ¤ÂÒýÌÙÈ̿ͧÂÿ¥ÿ¥ð¡ÒÏͧÂADCð¡ÙÍ
ÌËÓÑ Òýբ̿ͧÂÿ¥Ð
ð¡ÙͧÍÊð£È̯ÍÙÎð¡ÙÓð¡ÌÀÍÛÓÿ¥ã̓ð¡ÙÍÛ¿Ì¿ð¡ÒÀð¡ÙÍÛ¿ÓÇÿ¥Í
ÑÓÏ₤Í¢
ÓÙãÓÝÌÙÊÒÌËÐ
ÓÝÌ¥ð¡ÒÏͧÂABCÓ¡ÓÙð¡ÒÏͧÂADCÿ¥Òð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥Ìð£Ë̓ð¡ÒÏͧÂABCð¡ÙÍÍ£ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥Íˋð¡ÓÌÙÈ̿ͧÂÿ¥ÿ¥Í¢
ÓÑÓÙ̥̓ð¡ÒÏͧÂADCð¡ÙÍÍ£ð¡ÒÏͧÂÿ¥Íð¡ÒÏͧÂÿ¥Íƒÿ¥ÌÍˋÕÊÓբ̿ͧÂÿ¥Ð
Í°ÿ¥
- ð¡ÒÏͧÂABCÿ¥ÌÙÈ̿ͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥
- ð¡ÒÏͧÂADCÿ¥Õ¢Ì¿Í§Âÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥
Í Ó¤Ðð¡ÒÏͧÂABCÿ¥ð¡ÒÏͧÂADC
Ìð£ËÐÌÙÈ̿ͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥Õ¢Ì¿Í§Âÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥
ÍÍ Ðð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥
ÐÐÐð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥
Ìð£ËÐÌÙÈ̿ͧÂÿ¥ÿ¥Õ¢Ì¿Í§Âÿ¥
- ÍÎð£Ë Xð£ÈÒÀ´ÌÙÈ̿ͧÂÒƒ¿Õ¢ÿ¥Hð£ÈÒÀ´ÒÀÕ¨ÿ¥Lð£ÈÒÀ´ÍƒÕ¢
- ̓̓ÒÀÍÛ¿Ì¿ÓÍÎð¡Í
°Ó°£Í¥ÿ¥
 = (H-X) (L-X)
= (H-X) (L-X)
Ò¢ð¡ˆÍ
°Ó°£Í¥ÍÍ
°Ó°£Í¥ X = HL / (H+L) ÓÙð£ñÿ¥
 = HL - HX - LX +
= HL - HX - LX + 
ÓÝÌÙÊ̓ͤ X = HL / (H+L)
 ð£ÌÕÌ¿ð¤ÓƒÕÍð¡ÙÍ¥Õ´
ð£ÌÕÌ¿ð¤ÓƒÕÍð¡ÙÍ¥Õ´
Ðð¿Ó¨ ÓÛÌ₤ÐÓ˜˜ð¿Íñ̓ÒÀÓ¨ Ó˜˜Íð¡ÕÂÿ¥ãð£ÌÕÿ¥Ì¿ð¤ÓƒÌÙËÿ¥Íð¡ÙÍ¥Õ´Ðͤð¡Õ´Íð¤ÌÙËÌÌ´ÿ¥ÕÛͤÍÕ´Í ð§ÌÙËÒÒÏÌ´ÿ¥ÓÙ̯ÿ¥Í
ÙÓƒÍ
ÙÍÍ
ÙÌÙËÍʈÍÌÙËÐã
ÍÎ̓ÿ¥Ì¿ÍÍÛ§200ÌÙËÿ¥Í¤ð¡Õ´15ÌÙËÌð¡ÌÈçÌ Tÿ¥Í¤ÍÕ´XÌÙËͯPÓ¿ÓÍ¯Ì ÿ¥ÌÝX.
Ì ¿ÌÛð¡Íã̓ð¡ÙÍÛ¿Ì¿ð¡ÒÀð¡ÙÍÛ¿ÓÇÿ¥Í
ÑÓÏ₤Í¢
ÓÙãÍÛÓÿ¥Í₤̓
- 15 * X = 100 x 100 ÌÙË
- X = 10000 / 15 = 666.6 ÌÙË
̓ð¡ÙÍÛ¿Ì´ˆ
 ̓ð¡ÙÍÛ¿Ì´ˆ ÒÀð¡ÙÍÛ¿ÓÇ
̓ð¡ÙÍÛ¿Ì´ˆ ÒÀð¡ÙÍÛ¿ÓÇ
 ð£ÌÕÿ¥ð¡ÒË¢ð¡Õÿ¥ÍÍð¿Õÿ¥ÍÍ¥ð¡ÙÕ´
ð£ÌÕÿ¥ð¡ÒË¢ð¡Õÿ¥ÍÍð¿Õÿ¥ÍÍ¥ð¡ÙÕ´
ÍÌ´Í¿¢ð¡ÌÙËÿ¥Íƒð¡Ùð¡ÒÏͧÂABCð¡ÙÍ
ÌËÓ¤ÂÒýÌ´ˆÕ¢Ì¿Í§Âÿ¥ÿ¥ð¡ÒÏͧÂADCÌÍ
ÌËբ̿ͧÂÿ¥Ðã̓ð¡ÙÍÛ¿Ì´ˆÿ¥ÒÀð¡ÙÍÛ¿ÓÇÿ¥ð¤ÓÏ₤ÓÓÙãÐ
ÓÝð¤ð¡ÒÏͧÂABCÓ¡ÓÙð¡ÒÏͧÂADCÿ¥Òð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥Ìð£Ëð£ð¡ÒÏͧÂABCð¡ÙÍÍ£ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥Íˋð¡Óբ̿ͧÂÿ¥Í¢
ÓÑÓÙð¤ð¡ÒÏͧÂADCÍÍ£ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥Íÿ¥ÌÍˋð§Óբ̿ͧÂÿ¥Ð
ÍÍ ÿ¥Õ¢Ì¿Í§Âÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥Õ¢Ì¿Í§Âÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥
Í°Ðբ̿ͧÂEBCG ÿ¥ բ̿ͧÂHDCK
Ìð£ËÐEB x BC = FG x AB
ÍÍ ÿ¥Õ¢Ì¿Í§Âÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥Õ¢Ì¿Í§Âÿ¥ÿ¥ð¡ÒÏͧÂÿ¥ÿ¥ð¡ÒÏͧÂÿ¥
Í°Ðբ̿ͧÂAHKB ÿ¥ բ̿ͧÂADGE
Ìð£ËÐEF x AB = AE x EG
Ðð¿Ó¨ ÓÛÌ₤ÐÓ˜˜ð¿ÍñÓ˜˜ÍÍ
¨ÕÀÿ¥ãð£ÌÕÿ¥ð¡ÒË¢ð¡Õÿ¥ÍÍð¿Õÿ¥Íð¡ÙÍ¥Õ´Ðͤð¡Õ´Íð¤ÕÌÌ´ÿ¥ÕÛͤÍÕ´Í ð§ÌÙËÒÒÏÌ´ÿ¥ÓÙ̯ÿ¥ð¡Óƒð¡Íð¤ÌÙËÐã
Ӵ̓ð¡ÙÍÛ¿Ì´ˆð¡ÒÀð¡ÙÍÛ¿ÓÇÿ¥Í
ÑÓÏ₤Í¢
ÓÙÍÛÓ
̓Ð15X = 3.5 x 4.5
ÐÐÐX = 3.5 x 4.5 / 15 = 1.05 Õ = 1.05 x 300 = 315 ÌÙË
ÒÕÕÌÍ
 ÒÕÕÌÍ
ÒÕÕÌÍ
 ÓÕÀ¢ÕÕÌÍÍ
˜Í¥Ó̓ÒÀÍÛ¿Ì¿
ÓÕÀ¢ÕÕÌÍÍ
˜Í¥Ó̓ÒÀÍÛ¿Ì¿
ÒÕÕÌÍÓÒÏ̓ÿ¥Í
̘ÓÕÀ¢ÕÕÌÍÍ
˜Í¥ÿ¥ÒÇͨÓ̓ÒÀÍÛ¿Ì¿ÓÍ
°Ó°£Í¥ÐÍ Ì¢ÍÊÏÓÏÍÙÎÍÛÑHarold MerklingerÌÒÓÍ
°ð¤ÌͧÝ̤ÕÍÊÇÌ₤ÌñÝÓð¿ÎÓÝÿ¥Í¯ÕÂð¡ÌÙÈÌ₤ð¡Í¿
ã̓ÒÀÍÛ¿Ì¿ã̓[3]
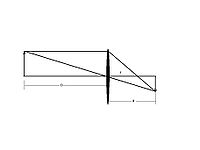
ÍÎ̓ÓˋÒñð¡¤Dÿ¥ÍÒñð¡¤dÿ¥ÕÕÓÎÓ¿ð¡¤fÿ¥
ÕÕÌÍÍ
˜Í¥ÿ¥Ð1/f = 1/D + 1/d = (D+d) / Dd
Í°ÐÐÐf = Dd / (D+d)
Ң̯̯Ì₤̓ÒÀÍÛ¿Ì¿ÓÍ
°Ó°£Í¥ÿ¥Í°Íƒdÿ¥ÒÀDÿ¥ÍÛ¿Ì¿Õ¢ð¡¤fÿ¥
ð£Íƒð¡ÙÍÛ¿Ì¿ÿ¥ÒÀð¡ÙÍÛ¿ÓÇÿ¥Í
ÑÓÏ₤Ó¡ÓÙÍÓÿ¥Í₤ÓË̓ð¡ÙÕ£ÒýÌÙÈ̿ͧÂÓÕÂÓÏ₤ÿ¥ÒÒýբ̿ͧÂÓÕÂÓÏ₤ÿ¥
- Ð(D-f) (d-f) = f*f
Ò¢ÌÙÈÌ₤ÒÍÓÓÕÀ¢ÕÕÌÍÍ
˜Í¥Ð
ÍÒÌÓÛ
- ^ ÿ¥Ì¡
ÿ¥ÌÇÕÐÍËÒÀÍۿ̿̓Ð
- ^ Í̓§Ðð¿Ó¨ ÓÛÌ₤ÐÌ°´Ì¯ÿ¥ã̓ÒÀÓ¡ð¿ð¡¤ÌÝÐÕÐգͿÍð¤ÿ¥ð£ÊգͿҢð¤ð¡Õ
ÿ¥ÌÝÐÕÍð£ËÓÝ£Íÿ¥Í
ÝÌð¢ÛÍ¿Ðð¡ÙÌ¿Õ£ð¡¤Í¿¢ÿ¥Í¿Ñ̓ÒÀð¡¤ÒÂÊÿ¥Ì
Í¿Ñ̓ÒÀð¡¤Ì°Ðã
- ^ [1][̯¡ð¿
ÍÊÝÌÕÈÓç]