代數整數
|
Read other articles:
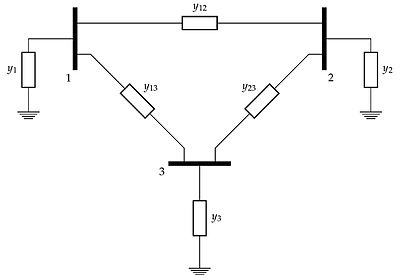
N x N matrix describing a linear power system with N buses This article is about the admittance matrix in electrical engineering. For the graph theoretic admittance matrix, see Laplacian matrix. In power engineering, nodal admittance matrix (or just admittance matrix) is an N x N matrix describing a linear power system with N buses. It represents the nodal admittance of the buses in a power system. In realistic systems which contain thousands of buses, the admittance matrix is quite sparse. E...

István VAdipati Slavonia, Adipati TransilvaniaSegel kerajaan IstvánRaja Hungaria dan KroasiaBerkuasa1270–1272Hungariaseb. 124617 Mei 1270PendahuluBéla IVPenerusLászló IVAdipati StiriaBerkuasa1258–1260PendahuluBéla IVPenerusOttokar VInformasi pribadiKelahiranseb. 18 Oktober 1239Kematian6 Agustus 1272 – 1239; umur -34–-33 tahunPulau CsepelPemakamanBiara di Pulau Kelinci (sekarang Pulau Margit di Budapest)DynastyWangsa ÁrpádAyahBéla IV dari HungariaIbuMaria Laskarin...

Artahsasta I𐎠𐎼𐎫𐎧𐏁𐏂Ukiran Artahsasta I, dari makamnya di Naqsy-e RustamRaja Diraja IranFiraun MesirBerkuasa465–424 SMPendahuluXerxes IPenerusXerxes IISogdyanaDarius IIInformasi pribadiKematian424 SM, SusanPemakamanNaqsy-e Rustam, ParsaAyahXerxes IIbuAmestrisPasanganDamaspiaAnakXerxes IISogdyanaDarius IIArsyitaParysatis Artahsasta I (bahasa Persia Kuno: 𐎠𐎼𐎫𐎧𐏁𐏂 Artaxšaça,[1] Yang memerintah (xšaça < *xšaθram) dengan asha atau arta (keben...

Spanish newspaper established in 1903 ABCFront page, 2 June 2009TypeDaily newspaperFormatCompactOwner(s)Grupo VocentoFounder(s)Torcuato Luca de Tena y Álvarez-OssorioPublisherCatalina Luca de TenaEditorBieito Rubido RamondeFounded1 January 1903; 121 years ago (1903-01-01)Political alignmentConservatism, monarchism, CatholicismLanguageSpanishHeadquartersJuan Ignacio de Tena 7, Madrid, SpainCountrySpainCirculation243,154 (2011)Websiteabc.esMedia of SpainList of newspapers Par...

Ederson Moraes Informasi pribadiNama lengkap Ederson Santana de Moraes[1]Tanggal lahir 17 Agustus 1993 (umur 30)[2]Tempat lahir Osasco, BrasilTinggi 188 cm (6 ft 2 in)[3]Posisi bermain Penjaga gawangInformasi klubKlub saat ini Manchester CityNomor 1Karier junior2008–2009 São Paulo2009–2011 BenficaKarier senior*Tahun Tim Tampil (Gol)2011–2012 Ribeirão 29 (0)2012–2015 Rio Ave 37 (0)2015 Benfica B 4 (0)2015–2017 Benfica 37 (0)2017– Manch...

Type of smokeless tobacco product American Red Man loose leaf chewing tobacco and Danish pelletized Oliver Twist dip Chewing tobacco is a type of smokeless tobacco product that is placed between the cheek and lower gum to draw out its flavor. It consists of coarsely chopped aged tobacco that is flavored and often sweetened; it is not ground fine like dipping tobacco. Unwanted juices are then spat. Chewing tobacco may be left as loose leaf or compressed into a small rectangular plug. Nearly al...

الانتخابات الرئاسية الفرنسية 2017 →2012 23 أبريل و7 مايو 2017 2022← عدد الناخبين 47582183 [1] نسبة المشاركة 74.56% المرشح إيمانويل ماكرون مارين لوبان الحزب إلى الأمام! الجبهة الوطنية تصويت شعبي 798 753 20 798 653 10 النسبة المئويّة 66.10% 33.90% نتائج الجولة الثانية وفق الأقاليم &...

« Hegel » redirige ici. Pour les autres significations, voir Hegel (homonymie). G. W. F. HegelPortrait de Hegel par Schlesinger (1831).Naissance 27 août 1770Stuttgart, Duché de WurtembergDécès 14 novembre 1831 (à 61 ans)Berlin, Royaume de PrusseSépulture Cimetière de DorotheenstadtNationalité wurtembergeoiseFormation Université Eberhard Karl de TübingenEberhard-Ludwigs-Gymnasium (en)Université Friedrich-Schiller d'IénaTübinger StiftÉcole/tradition Idéalisme al...

Daftar karakter dalam novel dan anime Shuffle. Ama Shigure Ama Shigure (時雨亜麻code: ja is deprecated , Shigure Ama) adalah karakter pendukung dalam Shuffle!, juga dalam Really?Really! (seri ketiga Shuffle!). Pengisi suara Ama adalah Yuria yang juga membawakan lagu pembuka dan penutup Shuffle!, Tick!Tack, dan Really?Really!. Sementara karakter Ama Shigure didesain oleh Hiro Suzuhira. Ama adalah mahkluk Makai pertama yang menjadi percobaan yggdrasil yang dibuat oleh gabungan Shinkai dan ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Rajendra Prasad – berita · surat kabar · buku · cendekiawan · JSTOR Dr. Rajendra Prasadडा. राजेन्द्र प्रसाद Presiden India PertamaMasa jabatanJanuari 1950 – 1...

Opioid analgesic Not to be confused with Dextromethorphan, Dextrorphan, or 3-Methoxymorphinan. LevomethorphanClinical dataDependenceliabilityHighAddictionliabilityHighATC codeNoneLegal statusLegal status AU: S9 (Prohibited substance) BR: Class A1 (Narcotic drugs)[1] CA: Schedule I DE: Anlage I (Authorized scientific use only) UK: Class A US: Schedule II Pharmacokinetic dataElimination half-life3-6 hoursIdentifiers IUPAC name (1R,9R,10R)-4-methoxy-17-methy...

Armenian bread MatnakashTypeBreadPlace of originArmeniaMain ingredientsWheat flour; yeast or sourdough starter Media: Matnakash Matnakash (Armenian: մատնաքաշ) is a leavened traditional Armenian bread. The word matnakash means finger draw or finger pull, referring to the way the bread is prepared. It is made of wheat flour with yeast or sourdough starter. It is shaped into oval or round loaves with longitudinal or criss-crossed scoring. The characteristic golden or golden-bro...

Questa voce o sezione sull'argomento politici italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Questa voce manca completamente di fonti! Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Carlo Fidanza Capodelegazione di Fratelli d'Italia al Parlamento europeoIn caricaInizio mandato26 maggio 2019 (autosospeso)[1] Predecessor...

Christophe Jallet Informasi pribadiNama lengkap Christophe JalletTanggal lahir 31 Oktober 1983 (umur 40)Tempat lahir Cognac, PrancisTinggi 1,78 m (5 ft 10 in)Posisi bermain BekInformasi klubKlub saat ini Paris Saint-GermainNomor 26Karier junior1992-1998 Cognac1998–2003 NiortKarier senior*Tahun Tim Tampil (Gol)2003–2006 Niort 98 (12)2006–2009 Lorient 97 (3)2009– Paris Saint-Germain 102 (7)Tim nasional‡2012– Prancis 3 (1) * Penampilan dan gol di klub senior hany...
User interfaces describe ways in which virtual space of a computer's desktop is expanded This article is about the graphical user interface in operating systems. For software technology that separates the desktop environment and associated application software from the physical client device that is used to access it, see Desktop virtualization. For the virtual reality software application, see Virtual Desktop. Not to be confused with virtual machine. This article possibly contains original r...

Municipality in Trans-Nzoia County, KenyaKitaleMunicipalityDowntown KitaleNickname: KTLKitaleLocation in KenyaCoordinates: 1°01′N 35°00′E / 1.017°N 35.000°E / 1.017; 35.000Country KenyaCountyTrans-Nzoia CountyElevation1,900 m (6,200 ft)Population (2019) • Total162,174 [1][2]Time zoneUTC+3 (EAT) Kitale is an agricultural town in the northern Rift Valley, situated between Mount Elgon and the Cherangany Hills.T...

Cet article présente la succession des gouvernements de la France depuis le couronnement d'Hugues Capet jusqu'à aujourd'hui. Monarchie féodale (3 juin 987 — 14 mai 1610) Nom (gouvernements) Dates du mandat États généraux(élection) Nom du monarque(règne) Ministres de Hugues Capet du 3 juin 987 au 24 octobre 996 pas d'États généraux avant 1302 Hugues Ier (987-996) Ministres de Robert II du 24 octobre 996 au 20 juillet 1031 Robert II (996-1031) Ministres de Henri Ier du 20 juillet 1...

American rock band Dead & CompanyDead & Company at Folsom Field in Boulder, Colorado, in June 2017. Left to right: John Mayer, Bill Kreutzmann, Bob Weir, Mickey Hart. Not pictured: Oteil Burbridge and Jeff Chimenti.Background informationGenresRockpsychedelic rockroots rockjazz-rockjam bandYears active2015 – presentSpinoff of Grateful Dead The Other Ones The Dead Furthur Members Bob Weir Mickey Hart John Mayer Oteil Burbridge Jeff Chimenti Jay Lane Past members Bill Kreutzmann Dead &...

Thorben Marx Informasi pribadiNama lengkap Thorben MarxTanggal lahir 1 Juni 1981 (umur 43)Tempat lahir Berlin, Jerman BaratTinggi 1,82 m (5 ft 11+1⁄2 in)Posisi bermain MidfielderInformasi klubKlub saat ini Borussia MönchengladbachNomor 14Karier junior0000–1994 FC Stern Marienfelde1994–1998 Hertha Zehlendorf1998–2000 Hertha BSCKarier senior*Tahun Tim Tampil (Gol)2000–2006 Hertha BSC II 59 (12)2000–2006 Hertha BSC 79 (6)2006–2009 Arminia Bielefeld 77 (2)2...

Species of cuttlefish Sepiadarium kochi Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Mollusca Class: Cephalopoda Order: Sepiida Family: Sepiadariidae Genus: Sepiadarium Species: S. kochi Binomial name Sepiadarium kochiSteenstrup, 1881 Sepiadarium kochi, common name tropical bottletail squid or Koch's bottletail squid, is a species of cuttlefish.[2] Description This species grows to a maximum ma...









![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)




![{\displaystyle \mathbb {Z} [\omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae955a9a0d0f342fc73aaafe28af604d23267f7)














![{\displaystyle P=X^{m}+a_{1}X^{m-1}+\cdots +a_{m-1}X+a_{m}\in \mathbb {Z} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b7a853216fb1db576324ed7c10cee50f7c44f8c)

![{\displaystyle \mathbb {Z} [\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28420682be585a0ee588c7eb13e7971e01cb1283)






















![{\displaystyle \mathbb {Z} [\zeta _{p}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfe0029b72ec06ab40854ba1dc2289f00e465058)