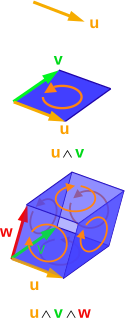
Tensör
|
Read other articles:

Dirty DeedsSutradaraDavid CaesarProduserBryan BrownDitulis olehDavid CaesarPemeranBryan BrownToni ColletteSam WorthingtonDistributorColumbia TriStarTanggal rilis18 Juli 2002 (2002-07-18)Durasi110 menitNegaraAustraliaBahasaInggrisAnggaranA$3 juta[butuh rujukan]PendapatankotorA$5 juta[1] Dirty Deeds adalah sebuah film 2002 yang dibuat di Australia. Film ini disutradarai oleh David Caesar dan dibintangi Bryan Brown, Toni Collette, Sam Neill, Sam Worthington dan John Goodman....

كورت كوخ معلومات شخصية تاريخ الميلاد 2 نوفمبر 1919 تاريخ الوفاة 9 نوفمبر 2000 (81 سنة) الجنسية ألمانيا تعديل مصدري - تعديل كورت كوخ (بالألمانية: Kurt Koch) هو مدرب كرة قدم ولاعب كرة قدم ألماني، ولد في 2 نوفمبر 1919، وتوفي في 9 نوفمبر 2000.[1] مراجع ^ معلومات عن كورت كوش (لاعب...

Gadis yang memakai celana jins pendek Celana pendek adalah bagian bawah pakaian bercabang dua yang umumnya digunakan perempuan dengan panjang di atas lutut.[1] Celana pendek dipakai di bagian pinggul, mengitari pinggang, dan menutupi kaki bagian atas.[2] Biasanya, ukuran celana lebih panjang sampai ke bawah lutut, tetapi celana pendek tidak menutupi seluruh panjang kaki, baik sebagai pakaian luar atau pun dalam. Hal ini membuat celana pendek nyaman dan mudah dipakai. Dinamakan...

García López de CárdenasGarcía López de Cárdenas menjelajahi Grand Canyon pada tahun 1540. Lukisan oleh Augusto Ferrer-DalmauLahirc. 1500Llerena, Badajoz, Kerajaan Kastila dan LeónMeninggalTanggal tidak diketahuiTempat tidak diketahuiKebangsaanSpanyolPekerjaanConquistadorDikenal atasOrang Eropa pertama yang menemukan Grand Canyon García López de Cárdenas y Figueroa adalah seorang conquistador dari Spanyol yang merupakan orang Eropa yang pertama kali menemukan Grand Canyon.[1 ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) الدوري الفرنسي الدرجة الثانية 1955–56 تفاصيل الموسم الدوري الفرنسي الدرجة الثانية النسخة 17 البلد فر...

Keuskupan Agung RosarioArchidioecesis RosariensisArquidiócesis de RosarioKatolik Basilika Katedral Bunda dari RosarioLokasiNegaraArgentinaProvinsi gerejawiRosarioStatistikLuas13.500 km2 (5.200 sq mi)Populasi- Total- Katolik(per 2010)1.854.0001,647,000 (88.8%)Paroki121InformasiDenominasiGereja KatolikRitusRitus RomaPendirian20 April 1934 (90 tahun lalu)KatedralBasilika Katedral Bunda dari RosarioPelindungBunda dari RosarioKepemimpinan kiniPausFransiskusUskup...

American novelist This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2021) (Learn how and when to remove this message) Julia PeterkinDoris Ulmann (left) and Peterkin (right)Born(1880-10-31)October 31, 1880Laurens County, South Carolina, U.S.DiedAugust 10, 1961(1961-08-10) (aged 80)EducationConverse University (BA, MA)OccupationAuthor Julia Peterkin...

Radio station in Egypt Lake–Tampa, Florida WTMPEgypt Lake, FloridaBroadcast areaTampa Bay AreaFrequency1150 kHz (HD Radio)BrandingWTMP AM 1150 102.1 FMProgrammingFormatUrban oldiesAffiliationsPremiere NetworksOwnershipOwnerNeal Ardman(NIA Broadcasting, Inc.)Sister stationsWTMP-FMHistoryFirst air dateDecember 1954; 69 years ago (1954-12).Call sign meaningTaMPaTechnical informationFacility ID74108ClassBPower10,000 watts day500 watts nightTranslator(s)102.1 W271DL (...

Pour les articles homonymes, voir Sciences Po. Institut d'études politiques de ParisL'entrée du 27 rue Saint-Guillaume.HistoireFondation 1872StatutType Grand établissement (EPSCP)[1]Forme juridique Établissement public national à caractère scientifique culturel et professionnel (d)Régime linguistique FrançaisFondateur Émile BoutmyDirecteur Jean BassèresMembre de Fondation nationale des sciences politiques, Conférence des grandes écoles (CGE)Site web www.sciencespo.frChiffres-clé...

伊恩·胡禮Ian Wright 個人信息本名 Ian Edward Wright[2]出生日期 (1963-11-03) 1963年11月3日(60歲)[1]出生地點 英国英格蘭伍利奇[1]位置 中鋒職業俱乐部*年份 球隊 出场 (进球)1985 Greenwich Borough(英语:Greenwich Borough F.C.) 1985–1991 水晶宫 225 (90)1991–1998 阿森纳 221 (128)1998–1999 西汉姆联 22 (9)1999 → 诺丁汉森林 (租借) 10 (5)1999–2000 凯尔特人 8 (3)2000 伯恩利 15 (4)�...

Giorgi Margvelashvili Presiden Georgia ke-4Masa jabatan17 November 2013 – 16 Desember 2018Perdana MenteriBidzina IvanishviliIrakli GaribashviliGiorgi KvirikashviliMamuka BakhtadzePendahuluMikheil SaakashviliPenggantiSalome ZurabishviliMenteri Pendidikan dan Ilmu PengetahuanMasa jabatan25 Oktober 2012 – 18 Juli 2013Perdana MenteriBidzina IvanishviliPendahuluKhatia DekanoidzePenggantiTamar Sanikidze Informasi pribadiLahir4 September 1969 (umur 54)Tbilisi, Uni Soviet(k...

Principati danubianiPrincipatul României Capitale Bucarest Governo Monarchia costituzionale Domnitor Alexandru Ioan Cuza (1851-66) Carlo I (1866-81) Lingua ufficiale Rumeno Esistenza 24 gennaio 1859 — 13 marzo 1881 Valuta Leu Stato successore Regno di Romania Principati di Moldavia e Valacchia nel 1786, mappa italiana di G. Pittori, tratta da cartografia di Giovanni Antonio Rizzi Zannoni. I Principati danubiani in un senso più ampio: Moldavia, Valacchia e Serbia Principati danubiani a me...

Questa voce sull'argomento edizioni di competizioni calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Campionato Primavera 1966-1967Campionato Primavera 1966-1967 Competizione Campionato Primavera Sport Calcio Edizione 5ª Organizzatore Lega Nazionale Professionisti Luogo Italia Risultati Vincitore Torino (Serie A) Verona (Assoluto)(1º e 1º titolo) Cronologia della competizione 1965-1966 1967-1968 Manuale Il Campi...

Word or phrase that refers to a specific color Color wheels with English color terms for RYB (above) and CMYK (below) approaches. A color term (or color name) is a word or phrase that refers to a specific color. The color term may refer to human perception of that color (which is affected by visual context) which is usually defined according to the Munsell color system, or to an underlying physical property (such as a specific wavelength of visible light). There are also numerical systems of ...

Rati Pandeyby FilmiTadka, 2012Lahir11 September 1982 (umur 42)Assam, IndiaTempat tinggalMumbai, Maharashtra, IndiaKebangsaanIndianAlmamaterMiranda House, Delhi UniversityPekerjaanaktris, pembawa acara, Penyanyi.Tahun aktif2006–sekarang Rati Pandey adalah aktris dan pembaw acara India. Pekerjaan televisinya yang terkenal termasuk Porus, Hitler Didi, Miley Jab Hum Tum, Begusarai, Har Ghar Kuch Kehta Hai dan Shaadi Street. Kehidupan awal dan latar belakang Rati Pandey lahir di Assam...

原尻の滝 沈堕の滝 岩戸の景観。百枝トンネルが貫き豊肥本線が通っている。 おおいた豊後大野ジオパーク(おおいたぶんごおおのジオパーク)は、大分県豊後大野市にあるジオパークである。2013年9月24日に日本ジオパークに認定され、日本ジオパークネットワークに加盟した[1]。 概要 豊後大野市は、大分県の南西部に位置し、大野川の中上流域に属する。この...

この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2010年7月) 正確性に疑問が呈されています。(2010年7月)出典検索?: 反日感情 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサー�...

GnatiaView of Gnatia and acropolis behindShown within ItalyLocationFasano, Province of Brindisi, Apulia, ItalyTypeSettlementSite notesWebsitewww.egnazia.eu Gnatia, Egnatia or Ignatia (Greek: Egnatia) was an ancient city of the Messapii, and their frontier town towards the Salentini. As Egnazia Appula, it was a medieval bishopric, which remains a Latin Catholic titular see. It is located near the modern Fasano, in Salento, the southern part of Puglia (Apulia) region in southern Italy. History ...

Village in Spain You can help expand this article with text translated from the corresponding article in Spanish. (August 2011) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into ...

Ethnic group native to the Balkans Not to be confused with Arameans, Armenians, or Romanians. Ethnic group AromaniansArmãnji, RrãmãnjiThe flag most commonly associated with the Aromanians,[1] unofficial but with traditional roots[2]Total populationc. 250,000 (Aromanian-speakers)[3]Regions with significant populations Greece39,855 (1951 census);[4] estimated up to 300,000 (2002)[5] Romania26,500 (2006 estimate)[6] North Macedoni...