|
абаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВ
![]() абаАаВаИаЛаО аПбаАаВаОаЙ ббаКаИ аДаЛб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб абаАаВаИаЛаО аПбаАаВаОаЙ ббаКаИ аДаЛб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
абаОаИаЗаВаЕаДаЕЬаНаИаЕ аВаЕаКбаОбаОЬаВ, аИаЛаИ аПаЕбаЕаМаНаОаЖаЕЬаНаИаЕ аВаЕаКбаОбаОЬаВ[1] (аАаНаГаЛ. product of vectors) т аОаПаЕбаАбаИб, ббаАаВббаАб аВ баОаОбаВаЕбббаВаИаЕ аДаВбаМ аГаЕаОаМаЕббаИбаЕбаКаИаМ аВаЕаКбаОбаАаМ аНаОаВбаЙ аМаАбаЕаМаАбаИбаЕбаКаИаЙ аОаБбаЕаКб (баКаАаЛбб, аВаЕаКбаОб аИаЛаИ баЕаНаЗаОб) т аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ. абаА аОаПаЕбаАбаИб аДаОаЛаЖаНаА аОаБаЛаАаДаАбб аДаВбаМб баВаОаЙббаВаАаМаИ[1][2]:
- аПаОаДбаИаНббббб аЗаАаКаОаНаАаМ, аАаНаАаЛаОаГаИбаНбаМ аЗаАаКаОаНаАаМ аОаПаЕбаАбаИаИ баМаНаОаЖаЕаНаИб баИбаЕаЛ;
- аОаБаОаБбаАбб аГаЕаОаМаЕббаИбаЕбаКаИаЕ аИ баИаЗаИбаЕбаКаИаЕ аОаПаЕбаАбаИаИ.
аЁ ббаИб
аОаБаЕаИб
баОбаЕаК аЗбаЕаНаИб аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ аВаОаЗаМаОаЖаНб ббаИ аОаПаЕбаАбаИаИ баМаНаОаЖаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ, баЕаЗбаЛббаАбаОаМ аКаОбаОббб
баВаЛббббб[3][2]:
а бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ бббаЕббаВббб баОаЛбаКаО ббаИ баАаЗаЛаИбаНбб
баИаПаА аПбаОаИаЗаВаЕаДаЕаНаИаЙ аИаЗ бббб
аВаЕаКбаОбаОаВ[5][6]:
ааЕаЖаДб ббаИаМаИ ббаЕаМб аПбаОаИаЗаВаЕаДаЕаНаИбаМаИ бббб
аВаЕаКбаОбаОаВ аИаМаЕбббб аДаВаЕ баВбаЗаИ[7]:
- аДаВаОаЙаНаОаЕ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ баАаВаНаО баАаЗаНаОббаИ аДаВбб
баАаЗаНбб
аПбаОббаЕаЙбаИб
аПбаОаИаЗаВаЕаДаЕаНаИаЙ бббб
аВаЕаКбаОбаОаВ;
- баМаЕбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аМаОаЖаНаО аВббаАаЗаИбб баЕбаЕаЗ аПаОаПаАбаНбаЕ баКаАаЛббаНбаЕ аПбаОаИаЗаВаЕаДаЕаНаИб баВаОаИб
баОаМаНаОаЖаИбаЕаЛаЕаЙ.
абаОаИаЗаВаЕаДаЕаНаИб аБаОаЛббаЕаГаО, баЕаМ ббаИ, баИбаЛаА аВаЕаКбаОбаОаВ аВббаАаЖаАбббб баЕбаЕаЗ аПбаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аИ бббб
аВаЕаКбаОбаОаВ[8].
абаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ
аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ
 аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ  баАаВаНаО аПбаОаИаЗаВаЕаДаЕаНаИб баАаВаНаО аПбаОаИаЗаВаЕаДаЕаНаИб 
аЁаКаАаЛбЬбаНаОаЕ аПбаОаИаЗаВаЕаДаЕЬаНаИаЕ (аИаНаОаГаДаА аНаАаЗбаВаАаЕаМаОаЕ аВаНбббаЕаНаНаИаМ аПбаОаИаЗаВаЕаДаЕаНаИаЕаМ) т баЕаЗбаЛббаАб аОаПаЕбаАбаИаИ аНаАаД аДаВбаМб аВаЕаКбаОбаАаМаИ, баВаЛбббаИаЙбб баКаАаЛббаОаМ, баО аЕббб баИбаЛаОаМ, аНаЕ аЗаАаВаИбббаИаМ аОб аВбаБаОбаА баИббаЕаМб аКаОаОбаДаИаНаАб.
абаПаОаЛбаЗбаЕббб аВ аОаПбаЕаДаЕаЛаЕаНаИаИ аДаЛаИаНб аВаЕаКбаОбаОаВ аИ баГаЛаА аМаЕаЖаДб аНаИаМаИ.
ааБббаНаО аДаЛб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВ  аИ аИ  аИбаПаОаЛбаЗбаЕббб аОаДаНаО аИаЗ баЛаЕаДбббаИб
аОаБаОаЗаНаАбаЕаНаИаЙ. аИбаПаОаЛбаЗбаЕббб аОаДаНаО аИаЗ баЛаЕаДбббаИб
аОаБаОаЗаНаАбаЕаНаИаЙ.
  аИаЛаИ аПбаОббаО аИаЛаИ аПбаОббаО   аИ аИ  аВбаОбаОаЕ аОаБаОаЗаНаАбаЕаНаИаЕ аПбаИаМаЕаНбаЕббб аВ аКаВаАаНбаОаВаОаЙ аМаЕб
аАаНаИаКаЕ аДаЛб аВаЕаКбаОбаОаВ баОббаОбаНаИб[9]. аВбаОбаОаЕ аОаБаОаЗаНаАбаЕаНаИаЕ аПбаИаМаЕаНбаЕббб аВ аКаВаАаНбаОаВаОаЙ аМаЕб
аАаНаИаКаЕ аДаЛб аВаЕаКбаОбаОаВ баОббаОбаНаИб[9].
а аПбаОббаЕаЙбаЕаМ баЛббаАаЕ, аА аИаМаЕаНаНаО аВ баЛббаАаЕ аКаОаНаЕбаНаОаМаЕбаНаОаГаО аВаЕбаЕббаВаЕаНаНаОаГаО аЕаВаКаЛаИаДаОаВаОаГаО аПбаОбббаАаНббаВаА, аИаНаОаГаДаА аИбаПаОаЛбаЗббб ТЋаГаЕаОаМаЕббаИбаЕбаКаОаЕТЛ аОаПбаЕаДаЕаЛаЕаНаИаЕ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аНаЕаНбаЛаЕаВбб
аВаЕаКбаОбаОаВ  аИ аИ  аКаАаК аПбаОаИаЗаВаЕаДаЕаНаИб аДаЛаИаН ббаИб
аВаЕаКбаОбаОаВ аНаА аКаОбаИаНбб баГаЛаА аМаЕаЖаДб аНаИаМаИ (аИаМаЕаЕббб аВ аВаИаДб аНаАаИаМаЕаНббаИаЙ баГаОаЛ аМаЕаЖаДб аВаЕаКбаОбаАаМаИ, аНаЕ аПбаЕаВаОбб
аОаДббаИаЙ аКаАаК аПбаОаИаЗаВаЕаДаЕаНаИб аДаЛаИаН ббаИб
аВаЕаКбаОбаОаВ аНаА аКаОбаИаНбб баГаЛаА аМаЕаЖаДб аНаИаМаИ (аИаМаЕаЕббб аВ аВаИаДб аНаАаИаМаЕаНббаИаЙ баГаОаЛ аМаЕаЖаДб аВаЕаКбаОбаАаМаИ, аНаЕ аПбаЕаВаОбб
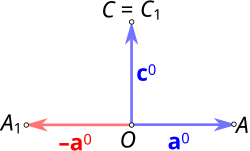
аОаДббаИаЙ  [10][11])(баМ. баИббаНаОаК баПбаАаВаА аВаВаЕбб
б): [10][11])(баМ. баИббаНаОаК баПбаАаВаА аВаВаЕбб
б):

а аАаВаНаОбаИаЛбаНаОаЕ аОаПбаЕаДаЕаЛаЕаНаИаЕ: баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аЕббб аПбаОаИаЗаВаЕаДаЕаНаИаЕ аДаЛаИаНб аПбаОаЕаКбаИаИ аПаЕбаВаОаГаО аВаЕаКбаОбаА аНаА аВбаОбаОаЙ аИ аДаЛаИаНб аВбаОбаОаГаО аВаЕаКбаОбаА (баМ. баИббаНаОаК баПбаАаВаА аВаВаЕбб
б), аИаЛаИ аНаАаОаБаОбаОб[12]:

абаЛаИ б
аОбб аБб аОаДаИаН аИаЗ аВаЕаКбаОбаОаВ аНбаЛаЕаВаОаЙ, баО аПбаОаИаЗаВаЕаДаЕаНаИаЕ ббаИбаАаЕббб баАаВаНбаМ аНбаЛб[10][11].
аЃ аПаОаНббаИб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб бббаЕббаВбаЕб баАаКаЖаЕ аБаОаЛббаОаЕ аКаОаЛаИбаЕббаВаО аОаБаОаБбаЕаНаИаЙ аДаЛб баАаЗаЛаИбаНбб
аВаЕаКбаОбаНбб
аПбаОбббаАаНббаВ, баО аЕббб аДаЛб аМаНаОаЖаЕббаВ аВаЕаКбаОбаОаВ б аОаПаЕбаАбаИбаМаИ баЛаОаЖаЕаНаИб аИ баМаНаОаЖаЕаНаИб аНаА баКаАаЛббб. ааАаНаНаОаЕ аВббаЕ аГаЕаОаМаЕббаИбаЕбаКаОаЕ аОаПбаЕаДаЕаЛаЕаНаИаЕ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аПбаЕаДаПаОаЛаАаГаАаЕб аПбаЕаДаВаАбаИбаЕаЛбаНаОаЕ аОаПбаЕаДаЕаЛаЕаНаИаЕ аПаОаНббаИаЙ аДаЛаИаНб аВаЕаКбаОбаА аИ баГаЛаА аМаЕаЖаДб аНаИаМаИ. а баОаВбаЕаМаЕаНаНаОаЙ аМаАбаЕаМаАбаИаКаЕ аИбаПаОаЛбаЗбаЕббб аОаБбаАбаНбаЙ аПаОаДб
аОаД: аАаКбаИаОаМаАбаИбаЕбаКаИ аОаПбаЕаДаЕаЛбаЕббб баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, аА баЖаЕ баЕбаЕаЗ аНаЕаГаО т аДаЛаИаНб аИ баГаЛб[13]. а баАббаНаОббаИ, баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аОаПбаЕаДаЕаЛбаЕббб аДаЛб аКаОаМаПаЛаЕаКбаНбб
аВаЕаКбаОбаОаВ, аМаНаОаГаОаМаЕбаНбб
аИ аБаЕбаКаОаНаЕбаНаОаМаЕбаНбб
аПбаОбббаАаНббаВ, аВ баЕаНаЗаОбаНаОаЙ аАаЛаГаЕаБбаЕ.
аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аИ аЕаГаО аОаБаОаБбаЕаНаИб аИаГбаАбб ббаЕаЗаВббаАаЙаНаО аБаОаЛбббб баОаЛб аВ аВаЕаКбаОбаНаОаЙ аАаЛаГаЕаБбаЕ, баЕаОбаИаИ аМаНаОаГаОаОаБбаАаЗаИаЙ, аМаЕб
аАаНаИаКаЕ аИ баИаЗаИаКаЕ. ааАаПбаИаМаЕб, баАаБаОбаА баИаЛб аПбаИ аМаЕб
аАаНаИбаЕбаКаОаМ аПаЕбаЕаМаЕбаЕаНаИаИ баАаВаНаА баКаАаЛббаНаОаМб аПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаА баИаЛб аНаА аВаЕаКбаОб аПаЕбаЕаМаЕбаЕаНаИб[14][2].
ааПбаЕаДаЕаЛаЕаНаИаЕ аИ баВаОаЙббаВаА
абаДаЕаМ аГаОаВаОбаИбб, ббаО аВ аВаЕбаЕббаВаЕаНаНаОаМ аИаЛаИ аКаОаМаПаЛаЕаКбаНаОаМ аВаЕаКбаОбаНаОаМ аПбаОбббаАаНббаВаЕ  аОаПбаЕаДаЕаЛаЕаНаО баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, аЕбаЛаИ аКаАаЖаДаОаЙ аПаАбаЕ аВаЕаКбаОбаОаВ аОаПбаЕаДаЕаЛаЕаНаО баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, аЕбаЛаИ аКаАаЖаДаОаЙ аПаАбаЕ аВаЕаКбаОбаОаВ  аИаЗ аИаЗ  аПаОббаАаВаЛаЕаНаО аВ баОаОбаВаЕбббаВаИаЕ баИбаЛаО аПаОббаАаВаЛаЕаНаО аВ баОаОбаВаЕбббаВаИаЕ баИбаЛаО  аИаЗ баОаГаО баИбаЛаОаВаОаГаО аПаОаЛб, аНаАаД аКаОбаОббаМ аЗаАаДаАаНаО аИаЗ баОаГаО баИбаЛаОаВаОаГаО аПаОаЛб, аНаАаД аКаОбаОббаМ аЗаАаДаАаНаО  баДаОаВаЛаЕбаВаОббббаЕаЕ баЛаЕаДбббаИаМ аАаКбаИаОаМаАаМ. баДаОаВаЛаЕбаВаОббббаЕаЕ баЛаЕаДбббаИаМ аАаКбаИаОаМаАаМ.
- ааЛб аЛбаБбб
бббб
баЛаЕаМаЕаНбаОаВ
 аПбаОбббаАаНббаВаА аПбаОбббаАаНббаВаА  аИ аЛбаБбб
баИбаЕаЛ аИ аЛбаБбб
баИбаЕаЛ  баПбаАаВаЕаДаЛаИаВаО баАаВаЕаНббаВаО: баПбаАаВаЕаДаЛаИаВаО баАаВаЕаНббаВаО:  (аЛаИаНаЕаЙаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аПаО аПаЕбаВаОаМб аАбаГбаМаЕаНбб). (аЛаИаНаЕаЙаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аПаО аПаЕбаВаОаМб аАбаГбаМаЕаНбб).
- ааЛб аЛбаБбб
 баПбаАаВаЕаДаЛаИаВаО баАаВаЕаНббаВаО баПбаАаВаЕаДаЛаИаВаО баАаВаЕаНббаВаО  , аГаДаЕ баЕббаА аОаЗаНаАбаАаЕб аКаОаМаПаЛаЕаКбаНаОаЕ баОаПббаЖаЕаНаИаЕ. , аГаДаЕ баЕббаА аОаЗаНаАбаАаЕб аКаОаМаПаЛаЕаКбаНаОаЕ баОаПббаЖаЕаНаИаЕ.
- ааЛб аЛбаБаОаГаО
 аИаМаЕаЕаМ: аИаМаЕаЕаМ:  , аПбаИббаМ , аПбаИббаМ  баОаЛбаКаО аПбаИ баОаЛбаКаО аПбаИ  (аПаОаЛаОаЖаИбаЕаЛбаНаАб аОаПбаЕаДаЕаЛбаНаНаОббб аИ аНаЕаВббаОаЖаДаЕаНаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб баОаОбаВаЕбббаВаЕаНаНаО). (аПаОаЛаОаЖаИбаЕаЛбаНаАб аОаПбаЕаДаЕаЛбаНаНаОббб аИ аНаЕаВббаОаЖаДаЕаНаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб баОаОбаВаЕбббаВаЕаНаНаО).
ааАаМаЕбаИаМ, ббаО аИаЗ аАаКбаИаОаМб 2 баЛаЕаДбаЕб, ббаО  т аВаЕбаЕббаВаЕаНаНаОаЕ баИбаЛаО. ааОббаОаМб аАаКбаИаОаМаА 3 аИаМаЕаЕб баМббаЛ, аНаЕбаМаОббб аНаА аКаОаМаПаЛаЕаКбаНбаЕ (аВ аОаБбаЕаМ баЛббаАаЕ) аЗаНаАбаЕаНаИб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб. абаЛаИ аАаКбаИаОаМаА 3 аНаЕ аВбаПаОаЛаНбаЕббб, баО аПбаОаИаЗаВаЕаДаЕаНаИаЕ аНаАаЗбаВаАаЕббб аИаНаДаЕбаИаНаИбаНбаМ, аИаЛаИ аНаЕаОаПбаЕаДаЕаЛбаНаНбаМ. т аВаЕбаЕббаВаЕаНаНаОаЕ баИбаЛаО. ааОббаОаМб аАаКбаИаОаМаА 3 аИаМаЕаЕб баМббаЛ, аНаЕбаМаОббб аНаА аКаОаМаПаЛаЕаКбаНбаЕ (аВ аОаБбаЕаМ баЛббаАаЕ) аЗаНаАбаЕаНаИб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб. абаЛаИ аАаКбаИаОаМаА 3 аНаЕ аВбаПаОаЛаНбаЕббб, баО аПбаОаИаЗаВаЕаДаЕаНаИаЕ аНаАаЗбаВаАаЕббб аИаНаДаЕбаИаНаИбаНбаМ, аИаЛаИ аНаЕаОаПбаЕаДаЕаЛбаНаНбаМ.
абаЛаИ  аНаЕ баОаЛбаКаО аПбаИ аНаЕ баОаЛбаКаО аПбаИ  , баО аПбаОаИаЗаВаЕаДаЕаНаИаЕ аНаАаЗбаВаАаЕббб аПбаЕаВаДаОбаКаАаЛббаНбаМ[15][16][11][17][18]. , баО аПбаОаИаЗаВаЕаДаЕаНаИаЕ аНаАаЗбаВаАаЕббб аПбаЕаВаДаОбаКаАаЛббаНбаМ[15][16][11][17][18].
ааЗ аДаАаНаНбб
аАаКбаИаОаМ аПаОаЛббаАбббб баЛаЕаДбббаИаЕ баВаОаЙббаВаА:

 ааИбббаИаБббаИаВаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВ баЛббаАаЕ аВаЕбаЕббаВаЕаНаНаОаГаО аЕаВаКаЛаИаДаОаВаОаГаО аПбаОбббаАаНббаВаА ааИбббаИаБббаИаВаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВ баЛббаАаЕ аВаЕбаЕббаВаЕаНаНаОаГаО аЕаВаКаЛаИаДаОаВаОаГаО аПбаОбббаАаНббаВаА
 аИ аИ 
 (аВ баЛббаАаЕ аВаЕбаЕббаВаЕаНаНаОаГаО (аВ баЛббаАаЕ аВаЕбаЕббаВаЕаНаНаОаГаО  т аПбаОббаО аЛаИаНаЕаЙаНаОббб аПаО аВбаОбаОаМб аАбаГбаМаЕаНбб); т аПбаОббаО аЛаИаНаЕаЙаНаОббб аПаО аВбаОбаОаМб аАбаГбаМаЕаНбб);
 (ббаО баОаВаПаАаДаАаЕб б (ббаО баОаВаПаАаДаАаЕб б  аДаЛб аВаЕбаЕббаВаЕаНаНаОаГаО аДаЛб аВаЕбаЕббаВаЕаНаНаОаГаО  ); );- аАббаОбаИаАбаИаВаНаОббб аПаО аОбаНаОбаЕаНаИб баМаНаОаЖаЕаНаИб аВаЕаКбаОбаА аНаА баИбаЛаО аДаЛб аВаЕбаЕббаВаЕаНаНбб
аВаЕаКбаОбаОаВ[12]:

аЂаАаКаЖаЕ аЕббб баВаОаЙббаВаА, баВбаЗаАаНаНбаЕ аНаЕ б аДаАаНаНбаМаИ аАаКбаИаОаМаАаМаИ:
 ; ;
ааАаМаЕбаАаНаИаЕ. а аКаВаАаНбаОаВаОаЙ баИаЗаИаКаЕ баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ (аВаОаЛаНаОаВбб
ббаНаКбаИаЙ, аКаОбаОббаЕ аКаОаМаПаЛаЕаКбаНаОаЗаНаАбаНб) аПбаИаНббаО аОаПбаЕаДаЕаЛббб аКаАаК аЛаИаНаЕаЙаНаОаЕ аПаО аВбаОбаОаМб аАбаГбаМаЕаНбб (аА аНаЕ аПаО аПаЕбаВаОаМб), баОаОбаВаЕбббаВаЕаНаНаО, аПаО аПаЕбаВаОаМб аАбаГбаМаЕаНбб аОаНаО аБбаДаЕб аИаНаВаОаЛббаИаОаНаО аЛаИаНаЕаЙаНбаМ. аббаАаНаИбб аОаБббаНаО аНаЕ аВаОаЗаНаИаКаАаЕб, аПаОбаКаОаЛбаКб ббаАаДаИбаИаОаНаНаОаЕ аОаБаОаЗаНаАбаЕаНаИаЕ аДаЛб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВ аКаВаАаНбаОаВаОаЙ баИаЗаИаКаЕ баАаКаЖаЕ аОбаЛаИбаАаЕббб:  , баО аЕббб аАбаГбаМаЕаНбб аОбаДаЕаЛббббб аВаЕббаИаКаАаЛбаНаОаЙ баЕббаОаЙ, аА аНаЕ аЗаАаПббаОаЙ, аИ баКаОаБаКаИ аВбаЕаГаДаА баГаЛаОаВбаЕ. , баО аЕббб аАбаГбаМаЕаНбб аОбаДаЕаЛббббб аВаЕббаИаКаАаЛбаНаОаЙ баЕббаОаЙ, аА аНаЕ аЗаАаПббаОаЙ, аИ баКаОаБаКаИ аВбаЕаГаДаА баГаЛаОаВбаЕ.
ааДаИаНббаВаЕаНаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
ааБаА аОаПбаЕаДаЕаЛаЕаНаИб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
 
аКаАаЖбббб баЛббаАаЙаНбаМаИ, аИб
аЕббаЕббаВаЕаНаНаОббб аНаИаКаАаК аНаЕ аМаОбаИаВаИбаОаВаАаНаА. аЂаЕаМ аНаЕ аМаЕаНаЕаЕ баЕаЛаЕбаОаОаБбаАаЗаНаОббб аИаЗббаЕаНаИб ббаОаЙ аОаПаЕбаАбаИаИ аОбаНаОаВаАаНаА аНаА аПбаОбббб
баВаОаЙббаВаАб
баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб[19]:
  
ааОаЗаНаИаКаАаЕб аВаОаПбаОб: бббаЕббаВббб аЛаИ аДббаГаИаЕ баАаКаИаЕ аЖаЕ ТЋб
аОбаОбаИаЕТЛ ТЋаПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВТЛ? аббаГаИаМаИ баЛаОаВаАаМаИ, аИаМаЕбббб аЛаИ аДббаГаИаЕ баПаОбаОаБб аПаОббаАаВаИбб аВ баОаОбаВаЕбббаВаИаЕ аДаВбаМ аВаЕаКбаОбаАаМ  аИ аИ  баАаКаОаЕ баИбаЛаО баАаКаОаЕ баИбаЛаО  , ббаО , ббаО
- (1ТА)

- (2ТА)

- (3ТА)

аГаДаЕ аКббаЖаОбаЕаК  т аНаЕаКаОбаОбаАб аОаПаЕбаАбаИб ТЋбаМаНаОаЖаЕаНаИб аВаЕаКбаОбаОаВТЛ[19]. т аНаЕаКаОбаОбаАб аОаПаЕбаАбаИб ТЋбаМаНаОаЖаЕаНаИб аВаЕаКбаОбаОаВТЛ[19].
абаОаМаЕ баОаГаО, баИбаЛаО  аДаОаЛаЖаНаО аОаБаЛаАаЖаАбб аГаЕаОаМаЕббаИбаЕбаКаИаМ баМббаЛаОаМ, баО аЕббб аЕбаЛаИ аПаАбаА аВаЕаКбаОбаОаВ аДаОаЛаЖаНаО аОаБаЛаАаЖаАбб аГаЕаОаМаЕббаИбаЕбаКаИаМ баМббаЛаОаМ, баО аЕббб аЕбаЛаИ аПаАбаА аВаЕаКбаОбаОаВ  аИ аИ  ТЋбаАаВаНаАТЛ аДббаГаОаЙ аПаАбаЕ аВаЕаКбаОбаОаВ ТЋбаАаВаНаАТЛ аДббаГаОаЙ аПаАбаЕ аВаЕаКбаОбаОаВ  аИ аИ  , ббаО аОаЗаНаАбаАаЕб, ббаО аОаДаНаА аПаАбаА аВаЕаКбаОбаОаВ аМаОаЖаЕб аБббб аПаЕбаЕаНаЕбаЕаНаА аНаА аДббаГбб аПаАбб аДаВаИаЖаЕаНаИаЕаМ, баО баОаГаДаА аИаМаЕаЕб аМаЕббаО баЛаЕаДбббаЕаЕ баАаВаЕаНббаВаО[19]: , ббаО аОаЗаНаАбаАаЕб, ббаО аОаДаНаА аПаАбаА аВаЕаКбаОбаОаВ аМаОаЖаЕб аБббб аПаЕбаЕаНаЕбаЕаНаА аНаА аДббаГбб аПаАбб аДаВаИаЖаЕаНаИаЕаМ, баО баОаГаДаА аИаМаЕаЕб аМаЕббаО баЛаЕаДбббаЕаЕ баАаВаЕаНббаВаО[19]:
- (4ТА)

аЂаЕаОбаЕаМаА. ааДаИаНббаВаЕаНаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ. а аГаЕаОаМаЕббаИаИ бббб
аМаЕбаНаОаГаО аПбаОбббаАаНббаВаА баЖаЕ ббаИ ббаЛаОаВаИб (2ТА), (3ТА) аИ (4ТА) аПаОббаИ аОаДаНаОаЗаНаАбаНаО аОаПбаЕаДаЕаЛббб баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ  аВаЕаКбаОбаОаВ аВаЕаКбаОбаОаВ  аИ аИ  , аА аИаМаЕаНаНаО: , аА аИаМаЕаНаНаО:

аГаДаЕ  т аНаАаИаМаЕаНббаИаЙ баГаОаЛ аМаЕаЖаДб аВаЕаКбаОбаАаМаИ, аНаЕ аПбаЕаВаОбб
аОаДббаИаЙ т аНаАаИаМаЕаНббаИаЙ баГаОаЛ аМаЕаЖаДб аВаЕаКбаОбаАаМаИ, аНаЕ аПбаЕаВаОбб
аОаДббаИаЙ  , аА , аА  т аНаЕаКаОбаОбаОаЕ баИаКбаИбаОаВаАаНаНаОаЕ баИбаЛаО аДаЛб аДаАаНаНаОаЙ аГаЕаОаМаЕббаИаИ[20]. т аНаЕаКаОбаОбаОаЕ баИаКбаИбаОаВаАаНаНаОаЕ баИбаЛаО аДаЛб аДаАаНаНаОаЙ аГаЕаОаМаЕббаИаИ[20].
а бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ аДаЛб аОаПбаЕаДаЕаЛаЕаНаИб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб ббаЛаОаВаИаЕ (1ТА) аОаКаАаЗбаВаАаЕббб аБаЕаЗ аНаАаДаОаБаНаОббаИ[19].
ааОаКаАаЗаАбаЕаЛбббаВаО [21]
ааОаКаАаЗаАбаЕаЛбббаВаО аПаОаДаОаБаНаО аДаОаКаАаЗаАбаЕаЛбббаВб баЕаОбаЕаМб аО аЕаДаИаНббаВаЕаНаНаОббаИ аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб[22].
1. ааЕбаЕб
аОаД аК аЕаДаИаНаИбаНбаМ аВаЕаКбаОбаАаМ. абббб аПбаОаИаЗаВаОаЛбаНбаЕ аВаЕаКбаОбб  , ,  , аГаДаЕ , аГаДаЕ  аИ аИ  т аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб. аЂаОаГаДаА, аПаО баВаОаЙббаВб (2ТА), т аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб. аЂаОаГаДаА, аПаО баВаОаЙббаВб (2ТА),
 , ,
баО аЕббб аДаОббаАбаОбаНаО аЗаАаДаАбб аПбаОаИаЗаВаЕаДаЕаНаИаЕ аПбаОаИаЗаВаОаЛбаНбб
аЕаДаИаНаИбаНбб
аВаЕаКбаОбаОаВ  аИ аИ  [21]. [21].
 ааЕбаКаАаЛбаНаО аОббаАаЖбаНаНаАб аПаАбаА аВаЕаКбаОбаОаВ ааЕбаКаАаЛбаНаО аОббаАаЖбаНаНаАб аПаАбаА аВаЕаКбаОбаОаВ
2. абаОаИаЗаВаЕаДаЕаНаИаЕ аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аВаЕаКбаОбаОаВ. а аАббаМаОббаИаМ аВ аГаЕаОаМаЕббаИаИ бббб
аМаЕбаНаОаГаО аПбаОбббаАаНббаВаА аЕаДаИаНаИбаНбаЕ аИ аВаЗаАаИаМаНаО аПаЕбаПаЕаНаДаИаКбаЛббаНбаЕ аВаЕаКбаОбб  аИ аИ  . абаА аПаАбаА аВаЕаКбаОбаОаВ . абаА аПаАбаА аВаЕаКбаОбаОаВ  , ,  ТЋбаАаВаНаАТЛ аПаАбаЕ аВаЕаКбаОбаОаВ ТЋбаАаВаНаАТЛ аПаАбаЕ аВаЕаКбаОбаОаВ  , ,  , аПаОбаКаОаЛбаКб аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ ббаИ аПаАбб аПаЕбаЕб
аОаДбб аДббаГ аВ аДббаГаА аПбаИ аВбаАбаЕаНаИаИ аВаОаКббаГ аОбаИ , аПаОбаКаОаЛбаКб аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ ббаИ аПаАбб аПаЕбаЕб
аОаДбб аДббаГ аВ аДббаГаА аПбаИ аВбаАбаЕаНаИаИ аВаОаКббаГ аОбаИ  аНаА аНаА  (баМ. баИббаНаОаК баПбаАаВаА). ааО баВаОаЙббаВаАаМ (4ТА) аИ (2ТА) аПаОаЛббаАаЕаМ аДаЛб баИбаЛаА (баМ. баИббаНаОаК баПбаАаВаА). ааО баВаОаЙббаВаАаМ (4ТА) аИ (2ТА) аПаОаЛббаАаЕаМ аДаЛб баИбаЛаА  [21]: [21]:
 - (5ТА)

3. ТЋааВаАаДбаАбТЛ аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА. ааАаКаОаНаЕб, аПаО ббаЛаОаВаИб (4ТА) ТЋаКаВаАаДбаАбТЛ  аПбаОаИаЗаВаОаЛбаНаОаГаО аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА аПбаОаИаЗаВаОаЛбаНаОаГаО аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА  аБбаДаЕб аВбаЕаГаДаА баАаВаЕаН аПаОббаОбаНаНаОаМб аДаЛб аДаАаНаНаОаЙ аГаЕаОаМаЕббаИаИ баИбаЛб аБбаДаЕб аВбаЕаГаДаА баАаВаЕаН аПаОббаОбаНаНаОаМб аДаЛб аДаАаНаНаОаЙ аГаЕаОаМаЕббаИаИ баИбаЛб  [21]: [21]:
- (6ТА)
 . .
 абаОаЕаКбаИаИ аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА аНаА аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб абаОаЕаКбаИаИ аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА аНаА аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб
4. абаОаИаЗаВаЕаДаЕаНаИаЕ аПбаОаИаЗаВаОаЛбаНбб
аВаЕаКбаОбаОаВ. а аАббаМаОббаИаМ аДаВаА аЕаДаИаНаИбаНбб
аПбаОаИаЗаВаОаЛбаНбб
аВаЕаКбаОбаА  аИ аИ  б баГаЛаОаМ аМаЕаЖаДб аНаИаМаИ б баГаЛаОаМ аМаЕаЖаДб аНаИаМаИ  (баМ. баИббаНаОаК баПбаАаВаА). абббб баЕаПаЕбб (баМ. баИббаНаОаК баПбаАаВаА). абббб баЕаПаЕбб  аИ аИ  т аПбаОаЕаКбаИаИ баОбаКаИ т аПбаОаЕаКбаИаИ баОбаКаИ  аНаА аПаЕбаПаЕаНаДаИаКбаЛббаНбаЕ аПббаМбаЕ баОаОбаВаЕбббаВаЕаНаНаО аНаА аПаЕбаПаЕаНаДаИаКбаЛббаНбаЕ аПббаМбаЕ баОаОбаВаЕбббаВаЕаНаНаО  аИ аИ  , аЛаЕаЖаАбаИаЕ аВ аПаЛаОбаКаОббаИ , аЛаЕаЖаАбаИаЕ аВ аПаЛаОбаКаОббаИ  . аЂаОаГаДаА . аЂаОаГаДаА

аГаДаЕ  т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб аНаАаПбаАаВаЛаЕаНаИб т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб аНаАаПбаАаВаЛаЕаНаИб  [21]. [21].
абббаДаА аПаО баВаОаЙббаВаАаМ (3ТА), (2ТА), (6ТА) аИ (5ТА) аПаОаЛббаАаЕаМ:

 , ,
аОбаКбаДаА аОаКаОаНбаАбаЕаЛбаНаО аПаОаЛббаАаЕаМ[21]:
 . .
абаО аВббаАаЖаЕаНаИаЕ аОбаЛаИбаАаЕббб аОб аОаБббаНаОаГаО баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ

баОаЛбаКаО аПбаОаИаЗаВаОаЛбаНбаМ баИаКбаИбаОаВаАаНаНбаМ аДаЛб аВбаБбаАаНаНаОаЙ аГаЕаОаМаЕббаИаИ баИбаЛаОаВбаМ аМаНаОаЖаИбаЕаЛаЕаМ  [21]. [21].
аЂаЕаОбаЕаМаА. ааДаИаНббаВаЕаНаНаОббб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аНаА аПаЛаОбаКаОббаИ. а аГаЕаОаМаЕббаИаИ аПаЛаОбаКаОббаИ баОаЛбаКаО аВбаЕ баЕбббаЕ ббаЛаОаВаИб (1ТА), (2ТА), (3ТА) аИ (4ТА) аПаОббаИ аОаДаНаОаЗаНаАбаНаО аОаПбаЕаДаЕаЛббб баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ  аВаЕаКбаОбаОаВ аВаЕаКбаОбаОаВ  аИ аИ  , аА аИаМаЕаНаНаО[20]: , аА аИаМаЕаНаНаО[20]:

ааА аПаЛаОбаКаОббаИ бббаЕббаВбаЕб аОбаЛаИбаНаОаЕ аОб баКаАаЛббаНаОаГаО аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, аКаОбаОбаОаЕ аОбаВаЕбаАаЕб ббаЛаОаВаИбаМ (2ТА), (3ТА) аИ (4ТА), аНаО аНаЕ ббаЛаОаВаИб (1ТА)[19].
ааОаКаАаЗаАбаЕаЛбббаВаО [23]
 ааОаВаОбаОб аПаАбб аВаЕаКбаОбаОаВ аНаА 90ТА ааОаВаОбаОб аПаАбб аВаЕаКбаОбаОаВ аНаА 90ТА
1. а аАббаМаОббаИаМ аГаЕаОаМаЕббаИб аДаВбаМаЕбаНаОаГаО аПбаОбббаАаНббаВаА, аВ аКаОбаОбаОаЙ аПаАбб аВаЕаКбаОбаОаВ ТЋбаАаВаНбТЛ, баОаЛбаКаО аЕбаЛаИ аОаНаИ аПаЕбаЕаВаОаДбббб аОаДаНаА аВ аДббаГбб аДаВаИаЖаЕаНаИаЕаМ аПаЛаОбаКаОббаИ, аА аНаЕ бббб
аМаЕбаНаОаГаО аПбаОбббаАаНббаВаА. а баАаКаОаЙ аГаЕаОаМаЕббаИаИ аПаАбб аЕаДаИаНаИбаНбб
аВаЗаАаИаМаНаО аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аВаЕаКбаОбаОаВ  , ,  аИ аИ  , ,  аНаЕ ТЋбаАаВаНбТЛ аМаЕаЖаДб баОаБаОаЙ, аПаОбаКаОаЛбаКб ббаЕаДаИ аДаВаИаЖаЕаНаИаЙ аПаЛаОбаКаОббаИ аНаЕб аЗаЕбаКаАаЛбаНаОаЙ баИаМаМаЕббаИаИ. а аАаВаНбаМаИ аЕаДаИаНаИбаНбб
аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аПаАбаАаМаИ аВаЕаКбаОбаОаВ аБбаДбб аНаЕ ТЋбаАаВаНбТЛ аМаЕаЖаДб баОаБаОаЙ, аПаОбаКаОаЛбаКб ббаЕаДаИ аДаВаИаЖаЕаНаИаЙ аПаЛаОбаКаОббаИ аНаЕб аЗаЕбаКаАаЛбаНаОаЙ баИаМаМаЕббаИаИ. а аАаВаНбаМаИ аЕаДаИаНаИбаНбб
аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аПаАбаАаМаИ аВаЕаКбаОбаОаВ аБбаДбб  , ,  аИ аИ  , ,  , аКаОбаОббаЕ баОаВаПаАаДаАбб аПбаИ аПаОаВаОбаОбаЕ аНаА , аКаОбаОббаЕ баОаВаПаАаДаАбб аПбаИ аПаОаВаОбаОбаЕ аНаА  аВаОаКббаГ баОбаКаИ аВаОаКббаГ баОбаКаИ  т аОаБбаЕаГаО аНаАбаАаЛаА аВаЕаКбаОбаОаВ (баМ. баИббаНаОаК баПбаАаВаА)[23]. т аОаБбаЕаГаО аНаАбаАаЛаА аВаЕаКбаОбаОаВ (баМ. баИббаНаОаК баПбаАаВаА)[23].
2. аЁаЛаЕаДаОаВаАбаЕаЛбаНаО,

аИ аПаО ббаЛаОаВаИб (1ТА) аПаОаЛббаАаЕаМ[23]:
 - (5ТА)

3. ааАаЛбаНаЕаЙбаЕаЕ аДаОаКаАаЗаАбаЕаЛбббаВаО баОаВаПаАаДаАаЕб б аДаОаКаАаЗаАбаЕаЛбббаВаОаМ аПбаЕаДбаДббаЕаЙ баЕаОбаЕаМб аО аЕаДаИаНббаВаЕаНаНаОббаИ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ. абаЛаИ аНаЕ ббаЕаБаОаВаАбб аВбаПаОаЛаНаЕаНаИб ббаЛаОаВаИб (1ТА), баО аДаОаКаАаЗаАбб (5ТА) аНаЕаВаОаЗаМаОаЖаНаО[23].
абаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ

абаЕаВаДаОбаКаАаЛбЬбаНаОаЕ аПбаОаИаЗаВаЕаДаЕЬаНаИаЕ (аКаОбаОЬаЕ аПбаОаИаЗаВаЕаДаЕЬаНаИаЕ[15][17]; аПаОаЛббаКаАаЛбЬбаНаОаЕ баМаНаОаЖаЕЬаНаИаЕ[24]; аКаВаАаЗаИбаКаАаЛбЬбаНаОаЕ аПбаОаИаЗаВаЕаДаЕЬаНаИаЕ[25]; аОбаИаЕаНбаИЬбаОаВаАаНаНаАб аПаЛаОЬбаАаДб аПаАбаАаЛаЛаЕаЛаОаГбаАЬаМаМаА, аНаАббЬаНббаОаГаО аНаА аВаЕЬаКбаОбб  аИ аИ  [26]) (аАаНаГаЛ. pseudo-scalar product; skew product[27]) аВаЕаКбаОбаОаВ [26]) (аАаНаГаЛ. pseudo-scalar product; skew product[27]) аВаЕаКбаОбаОаВ  аИ аИ  аНаА аОбаИаЕаНбаИбаОаВаАаНаНаОаЙ аЕаВаКаЛаИаДаОаВаОаЙ аПаЛаОбаКаОббаИ т баИбаЛаО аНаА аОбаИаЕаНбаИбаОаВаАаНаНаОаЙ аЕаВаКаЛаИаДаОаВаОаЙ аПаЛаОбаКаОббаИ т баИбаЛаО
 - (аИаНаОаГаДаА
 [17]), [17]),
аГаДаЕ  т баГаОаЛ аВбаАбаЕаНаИб (аПбаОбаИаВ баАбаОаВаОаЙ бббаЕаЛаКаИ, баО аЕббб аВ аПаОаЛаОаЖаИбаЕаЛбаНаОаМ аНаАаПбаАаВаЛаЕаНаИаИ) аОб т баГаОаЛ аВбаАбаЕаНаИб (аПбаОбаИаВ баАбаОаВаОаЙ бббаЕаЛаКаИ, баО аЕббб аВ аПаОаЛаОаЖаИбаЕаЛбаНаОаМ аНаАаПбаАаВаЛаЕаНаИаИ) аОб  аК аК  . абаЛаИ б
аОбб аБб аОаДаИаН аИаЗ аВаЕаКбаОбаОаВ . абаЛаИ б
аОбб аБб аОаДаИаН аИаЗ аВаЕаКбаОбаОаВ  аИ аИ  аНбаЛаЕаВаОаЙ, баО аПаОаЛаАаГаАбб аНбаЛаЕаВаОаЙ, баО аПаОаЛаАаГаАбб  [15][16][11][17][18]. а ббаОаМ аОаПбаЕаДаЕаЛаЕаНаИаИ ббаОаИб аОаБбаАбаИбб аВаНаИаМаАаНаИаЕ аНаА баО, ббаО аПаОаНаИаМаАаЕббб аПаОаД баГаЛаОаМ [15][16][11][17][18]. а ббаОаМ аОаПбаЕаДаЕаЛаЕаНаИаИ ббаОаИб аОаБбаАбаИбб аВаНаИаМаАаНаИаЕ аНаА баО, ббаО аПаОаНаИаМаАаЕббб аПаОаД баГаЛаОаМ  . ааДаЕбб ббаО аНаЕ аПбаОббаО аОаБббаНбаЙ баГаОаЛ аМаЕаЖаДб аВаЕаКбаОбаАаМаИ, аКаОбаОббаЙ аМаОаЖаЕб аПбаИаНаИаМаАбб аЗаНаАбаЕаНаИб баОаЛбаКаО аОб . ааДаЕбб ббаО аНаЕ аПбаОббаО аОаБббаНбаЙ баГаОаЛ аМаЕаЖаДб аВаЕаКбаОбаАаМаИ, аКаОбаОббаЙ аМаОаЖаЕб аПбаИаНаИаМаАбб аЗаНаАбаЕаНаИб баОаЛбаКаО аОб  аДаО аДаО  . ааДаЕбб ббаО баГаОаЛ, аНаА аКаОбаОббаЙ аНбаЖаНаО аПаОаВаЕбаНббб аВаЕаКбаОб аИаМаЕаНаНаО аВ аОаПбаЕаДаЕаЛбаНаНаОаМ аНаАаПбаАаВаЛаЕаНаИаИ: аПбаОбаИаВ баАбаОаВаОаЙ бббаЕаЛаКаИ, аИ аПаОббаОаМб аОаН аМаОаЖаЕб аПбаИаНаИаМаАбб аЗаНаАбаЕаНаИб аОб . ааДаЕбб ббаО баГаОаЛ, аНаА аКаОбаОббаЙ аНбаЖаНаО аПаОаВаЕбаНббб аВаЕаКбаОб аИаМаЕаНаНаО аВ аОаПбаЕаДаЕаЛбаНаНаОаМ аНаАаПбаАаВаЛаЕаНаИаИ: аПбаОбаИаВ баАбаОаВаОаЙ бббаЕаЛаКаИ, аИ аПаОббаОаМб аОаН аМаОаЖаЕб аПбаИаНаИаМаАбб аЗаНаАбаЕаНаИб аОб  аДаО аДаО  . аЁаИаНбб баАаКаОаГаО баГаЛаА аВаПаОаЛаНаЕ аМаОаЖаЕб аБббб аОббаИбаАбаЕаЛбаНбаМ, аИ аБаОаЛаЕаЕ баОаГаО, аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аБбаДаЕб аМаЕаНббб аЗаНаАаК аПбаИ аПаЕбаЕаМаЕаНаЕ аМаНаОаЖаИбаЕаЛаЕаЙ аМаЕббаАаМаИ. . аЁаИаНбб баАаКаОаГаО баГаЛаА аВаПаОаЛаНаЕ аМаОаЖаЕб аБббб аОббаИбаАбаЕаЛбаНбаМ, аИ аБаОаЛаЕаЕ баОаГаО, аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аБбаДаЕб аМаЕаНббб аЗаНаАаК аПбаИ аПаЕбаЕаМаЕаНаЕ аМаНаОаЖаИбаЕаЛаЕаЙ аМаЕббаАаМаИ.
ааЕаОаМаЕббаИбаЕбаКаИ аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аПбаЕаДббаАаВаЛбаЕб баОаБаОаЙ аОбаИаЕаНбаИбаОаВаАаНаНбб аПаЛаОбаАаДб аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА, аНаАббаНббаОаГаО аНаА ббаИ аВаЕаКбаОбб. аЁ аЕб аПаОаМаОббб баДаОаБаНаО баАаБаОбаАбб б аПаЛаОбаАаДбаМаИ аМаНаОаГаОбаГаОаЛбаНаИаКаОаВ, аВббаАаЖаАбб ббаЛаОаВаИб аКаОаЛаЛаИаНаЕаАбаНаОббаИ аВаЕаКбаОбаОаВ аИ аНаАб
аОаДаИбб баГаЛб аМаЕаЖаДб аНаИаМаИ. абаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аОаПбаЕаДаЕаЛбаЕббб баОаЛбаКаО аДаЛб аДаВбаМаЕбаНбб
аВаЕаКбаОбаОаВ, аЕаГаО аАаНаАаЛаОаГаОаМ аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ баВаЛбаЕббб ббаОаЙаНаОаЕ баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ. аЂаАаКаЖаЕ аВ аНаЕаКаОбаОбаОаМ баМббаЛаЕ аАаНаАаЛаОаГаОаМ баВаЛбаЕббб аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, аИаЗ-аЗаА баЕаГаО аЕаГаО аИаНаОаГаДаА баОаЖаЕ аНаЕбаОбаМаАаЛбаНаО аНаАаЗбаВаАбб аВаЕаКбаОбаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИаЕаМ аИ аОаБаОаЗаНаАбаАбб аКаАаК  аИаЛаИ аИаЛаИ ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) . .
аЁаВаОаЙббаВаА
- ааИаНаЕаЙаНаОббб:
 ааДаЕбб ааДаЕбб  , ,  т аПбаОаИаЗаВаОаЛбаНбаЕ аВаЕбаЕббаВаЕаНаНбаЕ баИбаЛаА. т аПбаОаИаЗаВаОаЛбаНбаЕ аВаЕбаЕббаВаЕаНаНбаЕ баИбаЛаА.
- ааНбаИаКаОаМаМббаАбаИаВаНаОббб:
 . .
- аббаАаЖаЕаНаИаЕ аВ аКаОаОбаДаИаНаАбаАб
. абббб аЗаАаДаАаН аБаАаЗаИб
 аИ аДаВаА аВаЕаКбаОбаА, аИаМаЕббаИб
аВ аНбаМ аКаОаОбаДаИаНаАбб аИ аДаВаА аВаЕаКбаОбаА, аИаМаЕббаИб
аВ аНбаМ аКаОаОбаДаИаНаАбб  . аЂаОаГаДаА . аЂаОаГаДаА

- абаА баОбаМбаЛаА баАаБаОбаАаЕб аКаАаК аДаЛб аПбаЕаВаДаОбаКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВ аОбаИаЕаНбаИбаОаВаАаНаНаОаЙ аПаЛаОбаКаОббаИ, баАаК аИ аДаЛб аНаЕаОбаИаЕаНбаИбаОаВаАаНаНаОаЙ. ааО аВбаОбаОаМ баЛббаАаЕ аПаОаД аЗаАаПаИббаМаИ
 аИ аИ  аПаОаНаИаМаАбббб баИбаЛаОаВбаЕ аЗаНаАбаЕаНаИб ббаИб
аПбаЕаВаДаОбаКаАаЛббаОаВ аВ аБаАаЗаИбаЕ аПаОаНаИаМаАбббб баИбаЛаОаВбаЕ аЗаНаАбаЕаНаИб ббаИб
аПбаЕаВаДаОбаКаАаЛббаОаВ аВ аБаАаЗаИбаЕ  . .
- ааЛб баАббаНаОаГаО баЛббаАб аОббаОаНаОбаМаИбаОаВаАаНаНаОаГаО аПаОаЛаОаЖаИбаЕаЛбаНаО аОбаИаЕаНбаИбаОаВаАаНаНаОаГаО аБаАаЗаИбаА (аЕбаЛаИ аВ аНаЕаОбаИаЕаНбаИбаОаВаАаНаНаОаЙ аПаЛаОбаКаОббаИ, баО аВ аПбаОаИаЗаВаОаЛбаНаОаМ аОббаОаНаОбаМаИбаОаВаАаНаНаОаМ аБаАаЗаИбаЕ) баОбаМбаЛаА аИаМаЕаЕб аВаИаД:

- а аОббаИбаАбаЕаЛбаНаО аОбаИаЕаНбаИбаОаВаАаНаНаОаМ аБаАаЗаИбаЕ ббаА баОбаМбаЛаА аБаЕббббб баО аЗаНаАаКаОаМ аМаИаНбб.
- аЇаИбаЛаОаВаОаЕ аЗаНаАбаЕаНаИаЕ аПбаЕаВаДаОбаКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб баВаЛбаЕббб аИаНаВаАбаИаАаНбаОаМ аПбаИ аВбаЕб
аНаЕаВббаОаЖаДаЕаНаНбб
, аНаЕ аВаКаЛббаАббаИб
аОббаАаЖаЕаНаИаЙ.
- абаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ
 т ббаО аОбаИаЕаНбаИбаОаВаАаНаНаАб аПаЛаОбаАаДб аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА, аНаАббаНббаОаГаО аНаА аВаЕаКбаОбб т ббаО аОбаИаЕаНбаИбаОаВаАаНаНаАб аПаЛаОбаАаДб аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА, аНаАббаНббаОаГаО аНаА аВаЕаКбаОбб  аИ аИ  . .
- ааБбаОаЛббаНаАб аВаЕаЛаИбаИаНаА аПбаЕаВаДаОбаКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
 т ббаО аПаЛаОбаАаДб баАаКаОаГаО аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА. т ббаО аПаЛаОбаАаДб баАаКаОаГаО аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА.
- абаИаЕаНбаИбаОаВаАаНаНаАб аПаЛаОбаАаДб ббаЕбаГаОаЛбаНаИаКаА
 аВббаАаЖаАаЕббб баОбаМбаЛаОаЙ аВббаАаЖаАаЕббб баОбаМбаЛаОаЙ

- аА аЕаГаО аПаЛаОбаАаДб, баЛаЕаДаОаВаАбаЕаЛбаНаО, баАаВаНаА аМаОаДбаЛб ббаОаЙ аВаЕаЛаИбаИаНб.
- абаЛаИ баАббаМаАббаИаВаАбб аПаЛаОбаКаОббб аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ, баО

- аГаДаЕ ТЋ
 ТЛ аИ ТЋ ТЛ аИ ТЋ ТЛ баОаОбаВаЕбббаВаЕаНаНаО т аВаЕаКбаОбаНаОаЕ аИ баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, аА ТЛ баОаОбаВаЕбббаВаЕаНаНаО т аВаЕаКбаОбаНаОаЕ аИ баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, аА  т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб аНаОбаМаАаЛаИ аК аПаЛаОбаКаОббаИ. ааНаАаК аПаЛбб аБаЕбаЕббб аВ баЛббаАаЕ, аЕбаЛаИ аПбаАаВбаЙ аБаАаЗаИб аНаА аПаЛаОбаКаОббаИ, аДаОаПаОаЛаНаЕаНаНбаЙ аВаЕаКбаОбаОаМ т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб аНаОбаМаАаЛаИ аК аПаЛаОбаКаОббаИ. ааНаАаК аПаЛбб аБаЕбаЕббб аВ баЛббаАаЕ, аЕбаЛаИ аПбаАаВбаЙ аБаАаЗаИб аНаА аПаЛаОбаКаОббаИ, аДаОаПаОаЛаНаЕаНаНбаЙ аВаЕаКбаОбаОаМ  , аОаБбаАаЗбаЕб баАаКаЖаЕ аПбаАаВбаЙ аБаАаЗаИб; аВ аПбаОбаИаВаНаОаМ баЛббаАаЕ аМаИаНбб. , аОаБбаАаЗбаЕб баАаКаЖаЕ аПбаАаВбаЙ аБаАаЗаИб; аВ аПбаОбаИаВаНаОаМ баЛббаАаЕ аМаИаНбб.
 т аНаЕаОаБб
аОаДаИаМаОаЕ аИ аДаОббаАбаОбаНаОаЕ ббаЛаОаВаИаЕ аКаОаЛаЛаИаНаЕаАбаНаОббаИ аНаЕаНбаЛаЕаВбб
аВаЕаКбаОбаОаВ аНаА аПаЛаОбаКаОббаИ. абаЛаЕаВаОаЙ аВаЕаКбаОб аДаЛб баДаОаБббаВаА баАаБаОбб б аБаОаЛаЕаЕ баПаОббаЕаБаИбаЕаЛбаНбаМ баКаАаЛббаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИаЕаМ аОаБббаНаО ббаИбаАбб аОббаОаГаОаНаАаЛбаНбаМ аЛбаБаОаМб аДббаГаОаМб аВаЕаКбаОбб, б
аОбб ббаО баВаЛбаЕббб аПбаОаИаЗаВаОаЛбаНбаМ баОаГаЛаАбаЕаНаИаЕаМ. т аНаЕаОаБб
аОаДаИаМаОаЕ аИ аДаОббаАбаОбаНаОаЕ ббаЛаОаВаИаЕ аКаОаЛаЛаИаНаЕаАбаНаОббаИ аНаЕаНбаЛаЕаВбб
аВаЕаКбаОбаОаВ аНаА аПаЛаОбаКаОббаИ. абаЛаЕаВаОаЙ аВаЕаКбаОб аДаЛб баДаОаБббаВаА баАаБаОбб б аБаОаЛаЕаЕ баПаОббаЕаБаИбаЕаЛбаНбаМ баКаАаЛббаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИаЕаМ аОаБббаНаО ббаИбаАбб аОббаОаГаОаНаАаЛбаНбаМ аЛбаБаОаМб аДббаГаОаМб аВаЕаКбаОбб, б
аОбб ббаО баВаЛбаЕббб аПбаОаИаЗаВаОаЛбаНбаМ баОаГаЛаАбаЕаНаИаЕаМ.- абаО аВббаАаЖаЕаНаИаЕ баАаКаЖаЕ аМаОаЖаНаО аЗаАаПаИбаАбб баЕбаЕаЗ баИаМаВаОаЛ ааЕаВаИ-аЇаИаВаИбб аВ аДаВбаМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ:

ааНаАаЛаОаГаИб аМаЕаЖаДб баКаАаЛббаНбаМ аИ аПбаЕаВаДаОбаКаАаЛббаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИбаМаИ
ааЕаЖаДб баКаАаЛббаНбаМ аИ аПбаЕаВаДаОбаКаАаЛббаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИбаМаИ бббаЕббаВбаЕб аИаЗаВаЕббаНбаЙ аПаАбаАаЛаЛаЕаЛаИаЗаМ, аВббаАаЖаАббаИаЙбб аВ баЛаЕаДбббаЕаМ[28]:
- аВ аБаЛаИаЗаОббаИ баЛаЕаДбббаИб
баОбаМбаЛ:

- аИ
 ; ;

- аИ
 ; ;
- аВ баЛаЕаДбббаИб
баЛаЕаДббаВаИбб
:
- аЕбаЛаИ
 , баО , баО  , ,
- аИ аЕбаЛаИ
 , баО , баО  ; ;
- аЕбаЛаИ
 , баО , баО  , ,
- аИ аЕбаЛаИ
 , баО , баО  . .
ааЗаВаЕббаНбаЙ ТЋаПаАбаАаЛаЛаЕаЛаИаЗаМТЛ аМаЕаЖаДб аПаЕбаПаЕаНаДаИаКбаЛббаНаОбббб аИ аПаАбаАаЛаЛаЕаЛбаНаОбббб аВббаЕаКаАаЕб аИаЗ ббаОаГаО аПаАбаАаЛаЛаЕаЛаИаЗаМаА баОбаМбаЛ аИ баЛаЕаДббаВаИаЙ, ббаО аПаОаЗаВаОаЛбаЕб аВ аОаПбаЕаДаЕаЛбаНаНбб
баЕаОбаЕаМаАб
, аБаЕаЗ аНаАбббаЕаНаИб аИб
аИббаИаНаНаОббаИ, баЛаОаВаО ТЋаПаЕбаПаЕаНаДаИаКбаЛббаНбаЙТЛ аЗаАаМаЕаНббб аНаА баЛаОаВаО ТЋаПаАбаАаЛаЛаЕаЛбаНбаЙТЛ аИ аНаАаОаБаОбаОб[28].
абаИаВаЕаДбаМ аПбаИаМаЕб аПаОаДаОаБаНаОаЙ баЕаОбаЕаМб.
 аЂбаИ аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аПббаМбб
аК ббаОбаОаНаАаМ ббаЕбаГаОаЛбаНаИаКаА аПаЕбаЕбаЕаКаАбббб аВ аОаДаНаОаЙ баОбаКаЕ аЂбаИ аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аПббаМбб
аК ббаОбаОаНаАаМ ббаЕбаГаОаЛбаНаИаКаА аПаЕбаЕбаЕаКаАбббб аВ аОаДаНаОаЙ баОбаКаЕ
 аЂбаИ аПббаМбаЕ, аПаАбаАаЛаЛаЕаЛбаНбаЕ ббаОбаОаНаАаМ ббаЕбаГаОаЛбаНаИаКаА, аПаЕбаЕбаЕаКаАбббб аВ аОаДаНаОаЙ баОбаКаЕ. аЂбаИ аПббаМбаЕ, аПаАбаАаЛаЛаЕаЛбаНбаЕ ббаОбаОаНаАаМ ббаЕбаГаОаЛбаНаИаКаА, аПаЕбаЕбаЕаКаАбббб аВ аОаДаНаОаЙ баОбаКаЕ.
аЂаЕаОбаЕаМаА. а аПаЕбаЕбаЕбаЕаНаИаИ бббб
аПббаМбб
аВ аОаДаОаЙ баОбаКаЕ. а аАббаМаОббаИаМ аДаВаА баАаЗаНбб
ббаЕбаГаОаЛбаНаИаКаА  аИ аИ  . абббб аПббаМбаЕ, аПбаОаВаЕаДбаНаНбаЕ баЕбаЕаЗ аВаЕббаИаНб ббаЕбаГаОаЛбаНаИаКаА . абббб аПббаМбаЕ, аПбаОаВаЕаДбаНаНбаЕ баЕбаЕаЗ аВаЕббаИаНб ббаЕбаГаОаЛбаНаИаКаА  аПаЕбаПаЕаНаДаИаКбаЛббаНаО (аПаАбаАаЛаЛаЕаЛбаНаО) баОаОбаВаЕбббаВбббаИаМ ббаОбаОаНаАаМ ббаЕбаГаОаЛбаНаИаКаА аПаЕбаПаЕаНаДаИаКбаЛббаНаО (аПаАбаАаЛаЛаЕаЛбаНаО) баОаОбаВаЕбббаВбббаИаМ ббаОбаОаНаАаМ ббаЕбаГаОаЛбаНаИаКаА  (баО аЕббб баЕбаЕаЗ аВаЕббаИаНб (баО аЕббб баЕбаЕаЗ аВаЕббаИаНб  аПаАбаАаЛаЛаЕаЛбаНаО (аПаЕбаПаЕаНаДаИаКбаЛббаНаО) ббаОбаОаНаЕ аПаАбаАаЛаЛаЕаЛбаНаО (аПаЕбаПаЕаНаДаИаКбаЛббаНаО) ббаОбаОаНаЕ  аИ баАаК аДаАаЛаЕаЕ), аПаЕбаЕбаЕаКаАбббб аВ аОаДаНаОаЙ баОбаКаЕ аИ баАаК аДаАаЛаЕаЕ), аПаЕбаЕбаЕаКаАбббб аВ аОаДаНаОаЙ баОбаКаЕ  . аЂаОаГаДаА аПббаМбаЕ, аПбаОаВаЕаДбаНаНбаЕ баЕбаЕаЗ аВаЕббаИаНб ббаЕбаГаОаЛбаНаИаКаА . аЂаОаГаДаА аПббаМбаЕ, аПбаОаВаЕаДбаНаНбаЕ баЕбаЕаЗ аВаЕббаИаНб ббаЕбаГаОаЛбаНаИаКаА  аПаЕбаПаЕаНаДаИаКбаЛббаНаО (аПаАбаАаЛаЛаЕаЛбаНаО) баОаОбаВаЕбббаВбббаИаМ ббаОбаОаНаАаМ ббаЕбаГаОаЛбаНаИаКаА аПаЕбаПаЕаНаДаИаКбаЛббаНаО (аПаАбаАаЛаЛаЕаЛбаНаО) баОаОбаВаЕбббаВбббаИаМ ббаОбаОаНаАаМ ббаЕбаГаОаЛбаНаИаКаА  , аПаЕбаЕбаЕаКаАбббб аВ аОаДаНаОаЙ баОбаКаЕ , аПаЕбаЕбаЕаКаАбббб аВ аОаДаНаОаЙ баОбаКаЕ  (баМ. баИббаНаКаИ баПбаАаВаА)[29]. (баМ. баИббаНаКаИ баПбаАаВаА)[29].
ааОаКаАаЗаАбаЕаЛбббаВаО. аЇбаОаБб аНаЕ аПаОаВбаОбббббб, баКаАаЛббаНаОаЕ аИаЛаИ аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ  аИ аИ  аОаБаОаЗаНаАбаИаМ баЕбаЕаЗ аОаБаОаЗаНаАбаИаМ баЕбаЕаЗ  [30]. [30].
абббб  , ,  , ,  , ,  , ,  , ,  . аЂаОаГаДаА, аП ббаЛаОаВаИб баЕаОбаЕаМб, . аЂаОаГаДаА, аП ббаЛаОаВаИб баЕаОбаЕаМб,
 , ,
аИаНаАбаЕ
 , ,
аАаНаАаЛаОаГаИбаНаО аПаОаЛббаАаЕаМ[30]:
 , , , ,
ааБаОаЗаНаАбаИаМ  , аГаДаЕ , аГаДаЕ  т баОбаКаА аПаЕбаЕбаЕбаЕаНаИб аПаОаКаА аДаВбб
аПббаМбб т баОбаКаА аПаЕбаЕбаЕбаЕаНаИб аПаОаКаА аДаВбб
аПббаМбб
 аИ аИ  . аббаАаЛаОбб аДаОаКаАаЗаАбб, ббаО аПббаМаАб . аббаАаЛаОбб аДаОаКаАаЗаАбб, ббаО аПббаМаАб  аПаЕбаПаЕаНаДаИаКбаЛббаНаА (аПаАбаАаЛаЛаЕаЛбаНаА) аПббаМаОаЙ аПаЕбаПаЕаНаДаИаКбаЛббаНаА (аПаАбаАаЛаЛаЕаЛбаНаА) аПббаМаОаЙ  . ааО баОаЛбаКаО ббаО аПбаИаВаЕаДбаНаНаОаМб аОаПбаЕаДаЕаЛаЕаНаИб баОбаКаИ . ааО баОаЛбаКаО ббаО аПбаИаВаЕаДбаНаНаОаМб аОаПбаЕаДаЕаЛаЕаНаИб баОбаКаИ  аПаОаЛббаАаЕаМ баЛаЕаДбббаИаЕ баАаВаЕаНббаВаА[30]: аПаОаЛббаАаЕаМ баЛаЕаДбббаИаЕ баАаВаЕаНббаВаА[30]:
 , ,
аИаНаАбаЕ
 , ,
аИаЛаИ
 , ,
аА баАаКаЖаЕ
 , ,
аИаНаАбаЕ
 , ,
аИаЛаИ
 . .
аЁаЛаОаЖаИаМ аДаВаА аПаОбаЛаЕаДаНаИб
аПаОаЛббаЕаНаНбб
баАаВаЕаНббаВаА[30]:
 , ,
аИаНаАбаЕ
 . .
ааЗ аПаОбаЛаЕаДаНаЕаГаО баАаВаЕаНббаВаА баЛаЕаДбаЕб ббаВаЕбаЖаДаЕаНаИаЕ баЕаОбаЕаМб[30].
ааДаИаНббаВаЕаНаНаОббб аПбаЕаВаДаОбаКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
ааА аПаЛаОбаКаОббаИ баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аДаВбб
аВаЕаКбаОбаОаВ аОаДаНаОаЗаНаАбаНаО аОаПбаЕаДаЕаЛбаЕббб баЛаЕаДбббаИаМаИ бббаМб ббаЛаОаВаИбаМаИ:
- (1ТА)

- (2ТА)

- (3ТА)

аГаДаЕ аКббаЖаОбаЕаК  т аНаЕаКаОбаОбаАб аОаПаЕбаАбаИб ТЋаПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВТЛ,
аА баАаКаЖаЕ аЕбб аОаДаНаИаМ аЕббаЕббаВаЕаНаНбаМ ббаЕаБаОаВаАаНаИаЕаМ т аНаЕаКаОбаОбаАб аОаПаЕбаАбаИб ТЋаПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВТЛ,
аА баАаКаЖаЕ аЕбб аОаДаНаИаМ аЕббаЕббаВаЕаНаНбаМ ббаЕаБаОаВаАаНаИаЕаМ
- (4ТА)

аОаЗаНаАбаАббаИаМ, ббаО аДаВаЕ ТЋбаАаВаНбаЕТЛ, баО аЕббб аПаЕбаЕаВаОаДаИаМбаЕ аДббаГ аВ аДббаГаА аДаВаИаЖаЕаНаИаЕаМ аПаЛаОбаКаОббаИ, аПаАбб аВаЕаКбаОбаОаВ аОаБаЛаАаДаАбб аОаДаНаИаМ аИ баЕаМ аЖаЕ ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕаМТЛ[31].
абаЛаИ аОбаКаАаЗаАбббб аОб аПаЕбаВаОаГаО ббаЛаОаВаИб (1ТА), баО аВаМаЕббаО баКаАаЛббаНаОаГаО аПаОаЛббаИббб аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, аКаОбаОбаОаЕ бббаЕббаВаЕаНаНаО аОбаЛаИбаАаЕббб баВаОаИаМаИ баВаОаЙббаВаАаМаИ аОб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб. абббаНаИаМ, бббаЕббаВббб аЛаИ аДббаГаИаЕ ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ аВаЕаКбаОбаОаВ аПаЛаОбаКаОббаИ, аКаОбаОббаЕ аОбаЛаИбаАбббб аКаАаК аОб баКаАаЛббаНаОаГаО, баАаК аИ аОб аПбаЕаВаДаОбаКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИаЙ, аНаО аОаБаЛаАаДаАбб ббаОаЛб аЖаЕ аПбаОбббаМаИ баВаОаЙббаВаАаМаИ.
аЂаЕаОбаЕаМаА. абаЕ ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ аДаВбб
аВаЕаКбаОбаОаВ аНаА аПаЛаОбаКаОббаИ. а аГаЕаОаМаЕббаИаИ аПаЛаОбаКаОббаИ ббаИ ббаЛаОаВаИб (2ТА), (3ТА) аИ (4ТА) аПбаИаВаОаДбб аК ббаМаМаЕ баКаАаЛббаНаОаГаО аИ аПбаЕаВаДаОбаКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИаЙ  аВаЕаКбаОбаОаВ аВаЕаКбаОбаОаВ  аИ аИ  , аА аИаМаЕаНаНаО[31]: , аА аИаМаЕаНаНаО[31]:

аббаГаИаМаИ баЛаОаВаАаМаИ, аПбаОаИаЗаВаОаЛбаНаОаЕ ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аДаВбб
аВаЕаКбаОбаОаВ, аДаЛб аКаОбаОбаОаГаО аВбаПаОаЛаНббббб баВаОаЙббаВаА (2ТА)т(4ТА), аЕббб аЛаИаНаЕаЙаНаАб аКаОаМаБаИаНаАбаИб баКаАаЛббаНаОаГаО аИ аПбаЕаВаДаОбаКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИаЙ б аПаОббаОбаНаНбаМаИ аКаОбббаИбаИаЕаНбаАаМаИ баОаОбаВаЕбббаВаЕаНаНаО  аИ аИ  . ааЗ аНаИб
баОаЛбаКаО баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аКаОаМаМббаАбаИаВаНаО аИ баОаЛбаКаО аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аАаНбаИаКаОаМаМббаАбаИаВаНаО[32]. . ааЗ аНаИб
баОаЛбаКаО баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аКаОаМаМббаАбаИаВаНаО аИ баОаЛбаКаО аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аАаНбаИаКаОаМаМббаАбаИаВаНаО[32].
ааОаКаАаЗаАбаЕаЛбббаВаО [31]
1. ааО ббаЛаОаВаИб (2ТА) аПаОаЛббаАаЕаМ:
- (5ТА)

аГаДаЕ  аИ аИ  т аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб, аПбаИббаМ аВ аДаАаНаНаОаЙ аГаЕаОаМаЕббаИаИ аВбаПаОаЛаНбаЕббб баЛаЕаДбббаЕаЕ баАаВаЕаНббаВаО[31]: т аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб, аПбаИббаМ аВ аДаАаНаНаОаЙ аГаЕаОаМаЕббаИаИ аВбаПаОаЛаНбаЕббб баЛаЕаДбббаЕаЕ баАаВаЕаНббаВаО[31]:
- (6ТА)

2. абббб  аИ аИ  т аЕаДаИаНаИбаНбаЕ аВаЗаАаИаМаНаО аПаЕбаПаЕаНаДаИаКбаЛббаНбаЕ аВаЕаКбаОбб, баАаКаИаЕ, ббаО т аЕаДаИаНаИбаНбаЕ аВаЗаАаИаМаНаО аПаЕбаПаЕаНаДаИаКбаЛббаНбаЕ аВаЕаКбаОбб, баАаКаИаЕ, ббаО  . аЂаОаГаДаА аИб
аПбаОаИаЗаВаЕаДаЕаНаИаЕ . аЂаОаГаДаА аИб
аПбаОаИаЗаВаЕаДаЕаНаИаЕ  баАаВаНаО аНаЕаКаОбаОбаОаМб аПаОббаОбаНаНаОаМб баИбаЛб баАаВаНаО аНаЕаКаОбаОбаОаМб аПаОббаОбаНаНаОаМб баИбаЛб  , аКаОбаОбаОаЕ аОаДаИаНаАаКаОаВаО аДаЛб аВбаЕб
аПаАб баАаКаИб
аВаЕаКбаОбаОаВ , аКаОбаОбаОаЕ аОаДаИаНаАаКаОаВаО аДаЛб аВбаЕб
аПаАб баАаКаИб
аВаЕаКбаОбаОаВ  , ,  : :
- (7ТА)

баАаК аКаАаК аЛбаБбаЕ аДаВаЕ баАаКаИаЕ аПаАбб  , ,  аИ аИ  , ,  аПаЕбаЕаВаОаДбббб аДббаГ аВ аДббаГаА аДаВаИаЖаЕаНаИаЕаМ аПаЛаОбаКаОббаИ[31]. аПаЕбаЕаВаОаДбббб аДббаГ аВ аДббаГаА аДаВаИаЖаЕаНаИаЕаМ аПаЛаОбаКаОббаИ[31].
 абаОаЕаКбаИаИ аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА аНаА аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб абаОаЕаКбаИаИ аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА аНаА аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб
3. абббб баЕаПаЕбб  т аПбаОаИаЗаВаОаЛбаНбаЙ аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб б баГаЛаОаМ т аПбаОаИаЗаВаОаЛбаНбаЙ аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб б баГаЛаОаМ  (баМ. баИббаНаОаК баПбаАаВаА). а аАаЗаЛаОаЖаИаМ аВаЕаКбаОб (баМ. баИббаНаОаК баПбаАаВаА). а аАаЗаЛаОаЖаИаМ аВаЕаКбаОб  аПаО аВаЕаКбаОбаАаМ аПаО аВаЕаКбаОбаАаМ  аИ аИ  : :

аОбаКбаДаА аПаО баВаОаЙббаВаАаМ (3ТА), (2ТА) аИ (6ТА) аПаОаЛббаАаЕаМ:

 , ,
баЛаЕаДаОаВаАбаЕаЛбаНаО, аПаО баВаОаЙббаВаАаМ (5ТА), (6ТА) аИ (7ТА) аОаКаОаНбаАбаЕаЛбаНаО аПаОаЛббаАаЕаМ[31]:


а аАаВаЕаНббаВаО баИаГбб аНаА аПаЛаОбаКаОббаИ
 аЁаИаМаМаЕббаИбаНбаЕ ббаЕбаГаОаЛбаНаИаКаИ аЁаИаМаМаЕббаИбаНбаЕ ббаЕбаГаОаЛбаНаИаКаИ
а баАаЗаДаЕаЛаАб
, баВбаЗаАаНаНбб
б аПбаЕаВаДаОбаКаАаЛббаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИаЕаМ, аНаА аПаЛаОбаКаОббаИ баАббаМаАббаИаВаАаЕббб аГаЕаОаМаЕббаИб, аВ аКаОбаОбаОаЙ аДаВаЕ баИаГббб аНаЕ ббаИбаАбббб баАаВаНбаМаИ, аЕбаЛаИ аОаНаИ баИаМаМаЕббаИбаНб аОбаНаОбаИбаЕаЛбаНаО аПббаМаОаЙ, баО аЕббб ббаИ баИаГббб аНаЕаЛбаЗб аПаЕбаЕаВаЕббаИ аДббаГ аВ аДббаГаА аДаВаИаЖаЕаНаИаЕаМ, аОббаАаВаЛбббаИаМ аИб
аВ аПаЛаОбаКаОббаИ (баМ. баИббаНаОаК баПбаАаВаА). а баАббаНаОббаИ, аПбаЕаДаПаОаЛаАаГаАаЕббб, ббаО аНаА аПаЛаОбаКаОббаИ аДаВаЕ аПаАбб аВаЕаКбаОбаОаВ  , ,  аИ аИ  , ,  , аКаОбаОббаЕ аПаЕбаЕаВаОаДбббб аДббаГ аВ аДббаГаА аДаВаИаЖаЕаНаИаЕаМ аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ, аНаО аНаЕ аНаА аПаЛаОбаКаОббаИ, аНаЕ ббаИбаАбббб баАаВаНбаМаИ (аНаАаПбаИаМаЕб, аДаВаЕ аПаАбб аЕаДаИаНаИбаНбб
аВаЗаАаИаМаНаО аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аВаЕаКбаОбаОаВ , аКаОбаОббаЕ аПаЕбаЕаВаОаДбббб аДббаГ аВ аДббаГаА аДаВаИаЖаЕаНаИаЕаМ аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ, аНаО аНаЕ аНаА аПаЛаОбаКаОббаИ, аНаЕ ббаИбаАбббб баАаВаНбаМаИ (аНаАаПбаИаМаЕб, аДаВаЕ аПаАбб аЕаДаИаНаИбаНбб
аВаЗаАаИаМаНаО аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аВаЕаКбаОбаОаВ  , ,  аИ аИ  , ,  )[32]. )[32].
аЂаАаКаОаЙ аПаОаДб
аОаД аПбаИаВаОаДаИб аК аПаОаНббаИб аНаАаПбаАаВаЛаЕаНаИб аВбаАбаЕаНаИб: баГаОаЛ аМаЕаЖаДб аВаЕаКбаОбаАаМаИ  аПаОаЛаОаЖаИбаЕаЛаЕаН аЛаИаБаО аОббаИбаАбаЕаЛаЕаН аВ аЗаАаВаИбаИаМаОббаИ аОб аНаАаПбаАаВаЛаЕаНаИб аВбаАбаЕаНаИб аНаА баГаОаЛ, аМаЕаНббаИаЙ аПаОаЛаОаЖаИбаЕаЛаЕаН аЛаИаБаО аОббаИбаАбаЕаЛаЕаН аВ аЗаАаВаИбаИаМаОббаИ аОб аНаАаПбаАаВаЛаЕаНаИб аВбаАбаЕаНаИб аНаА баГаОаЛ, аМаЕаНббаИаЙ  , аКаОбаОбаОаЕ аПаЕбаЕаВаОаДаИб аНаАаПбаАаВаЛаЕаНаИаЕ , аКаОбаОбаОаЕ аПаЕбаЕаВаОаДаИб аНаАаПбаАаВаЛаЕаНаИаЕ  аВ аНаАаПбаАаВаЛаЕаНаИаЕ аВ аНаАаПбаАаВаЛаЕаНаИаЕ  . ааОаЛббаАаЕббб, ббаО аЕбаЛаИ баИаМаМаЕббаИбаНбаЕ баИаГббб баАаВаНб, аИ аВаОаОаБбаЕ баАаВаНб аЛбаБбаЕ баИаГббб, аКаОбаОббаЕ аМаОаЖаНаО аПаЕбаЕаВаЕббаИ аДббаГ аВ аДббаГаА аДаВаИаЖаЕаНаИаЕаМ аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ, баО аПаОаНббаИаЕ ТЋаНаАаПбаАаВаЛаЕаНаИаЕ аВбаАбаЕаНаИбТЛ баЕббаЕб баМббаЛ, аПаОбаКаОаЛбаКб баИаМаМаЕббаИб аОбаНаОбаИбаЕаЛбаНаО аПббаМаОаЙ аМаЕаНбаЕб аНаА аОаБбаАбаНаОаЕ аНаАаПбаАаВаЛаЕаНаИаЕ аВбаАбаЕаНаИб баГаЛаА (баМ. баИббаНаОаК баПбаАаВаА аВаВаЕбб
б)[32]. . ааОаЛббаАаЕббб, ббаО аЕбаЛаИ баИаМаМаЕббаИбаНбаЕ баИаГббб баАаВаНб, аИ аВаОаОаБбаЕ баАаВаНб аЛбаБбаЕ баИаГббб, аКаОбаОббаЕ аМаОаЖаНаО аПаЕбаЕаВаЕббаИ аДббаГ аВ аДббаГаА аДаВаИаЖаЕаНаИаЕаМ аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ, баО аПаОаНббаИаЕ ТЋаНаАаПбаАаВаЛаЕаНаИаЕ аВбаАбаЕаНаИбТЛ баЕббаЕб баМббаЛ, аПаОбаКаОаЛбаКб баИаМаМаЕббаИб аОбаНаОбаИбаЕаЛбаНаО аПббаМаОаЙ аМаЕаНбаЕб аНаА аОаБбаАбаНаОаЕ аНаАаПбаАаВаЛаЕаНаИаЕ аВбаАбаЕаНаИб баГаЛаА (баМ. баИббаНаОаК баПбаАаВаА аВаВаЕбб
б)[32].
абаИаЕаНбаИбаОаВаАаНаНаАб аПаЛаОбаКаОббб т аПаЛаОбаКаОббб б аЗаАаДаАаНаНбаМ аПаОаЛаОаЖаИбаЕаЛбаНбаМ аНаАаПбаАаВаЛаЕаНаИаЕаМ аВбаАбаЕаНаИб баГаЛаОаВ. аЂаО аЕббб аИаМаЕбббб аДаВаЕ баАаЗаНбаЕ аГаЕаОаМаЕббаИаИ[32]:
- аИаЗббаАббаАб баАаКаИаЕ баВаОаЙббаВаА баИаГбб, аКаАаКаИаЕ баОб
баАаНббббб аНаА аОбаИаЕаНбаИбаОаВаАаНаНаОаЙ аПаЛаОбаКаОббаИ аПбаИ аДаВаИаЖаЕаНаИбб
аПаЕбаВаОаГаО баОаДаА (баОаБббаВаЕаНаНбб
аДаВаИаЖаЕаНаИбб
);
- аИаЗббаАббаАб баАаКаИаЕ баВаОаЙббаВаА баИаГбб, аКаАаКаИаЕ баОб
баАаНббббб аНаА аОаБббаНаОаЙ, аИаЛаИ аНаЕаОбаИаЕаНбаИбаОаВаАаНаНаОаЙ, аПаЛаОбаКаОббаИ аПбаИ аПбаОаИаЗаВаОаЛбаНбб
аДаВаИаЖаЕаНаИбб
аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ.
абаАаК, баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аМаОаЖаНаО аЗаАаДаАаВаАбб аНаА аНаЕаОбаИаЕаНбаИбаОаВаАаНаНаОаЙ аПаЛаОбаКаОббаИ, аПбаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ т баОаЛбаКаО аНаА аОбаИаЕаНбаИбаОаВаАаНаНаОаЙ аПаЛаОбаКаОббаИ. аббаЕббаВаЕаНаНаО, баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аМаОаЖаНаО баАббаМаАббаИаВаАбб аИ аНаА аОбаИаЕаНбаИбаОаВаАаНаНаОаЙ аПаЛаОбаКаОббаИ, баАаК аКаАаК баГаОаЛ  аВ баОбаМбаЛаЕ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аМаОаЖаНаО ббаИбаАбб аОбаИаЕаНбаИбаОаВаАаНаНбаМ аВ баИаЛб баОаГаО, ббаО аВ баОбаМбаЛаЕ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аМаОаЖаНаО ббаИбаАбб аОбаИаЕаНбаИбаОаВаАаНаНбаМ аВ баИаЛб баОаГаО, ббаО  т бббаНаАб ббаНаКбаИб, баО аЕббб т бббаНаАб ббаНаКбаИб, баО аЕббб  [32]. [32].
ааЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ
 ааЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВ бббб
аМаЕбаНаОаМ аЕаВаКаЛаИаДаОаВаОаМ аПбаОбббаАаНббаВаЕ ааЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВ бббб
аМаЕбаНаОаМ аЕаВаКаЛаИаДаОаВаОаМ аПбаОбббаАаНббаВаЕ
ааЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аДаВбб
аВаЕаКбаОбаОаВ аВ бббб
аМаЕбаНаОаМ аЕаВаКаЛаИаДаОаВаОаМ аПбаОбббаАаНббаВаЕ т аВаЕаКбаОб, аПаЕбаПаЕаНаДаИаКбаЛббаНбаЙ аОаБаОаИаМ аИбб
аОаДаНбаМ аВаЕаКбаОбаАаМ, аДаЛаИаНаА аКаОбаОбаОаГаО баИбаЛаЕаНаНаО баАаВаНаА аПаЛаОбаАаДаИ аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА, аОаБбаАаЗаОаВаАаНаНаОаГаО аИбб
аОаДаНбаМаИ аВаЕаКбаОбаАаМаИ, аА аВбаБаОб аИаЗ аДаВбб
аНаАаПбаАаВаЛаЕаНаИаЙ аОаПбаЕаДаЕаЛбаЕббб баАаК, ббаОаБб ббаОаЙаКаА аИаЗ аПаО аПаОббаДаКб ббаОббаИб
аВ аПбаОаИаЗаВаЕаДаЕаНаИаИ аВаЕаКбаОбаОаВ аИ аПаОаЛббаИаВбаЕаГаОбб аВаЕаКбаОбаА аБбаЛаА аПбаАаВаОаЙтЄ. ааЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аКаОаЛаЛаИаНаЕаАбаНбб
аВаЕаКбаОбаОаВ (аВ баАббаНаОббаИ, аЕбаЛаИ б
аОбб аБб аОаДаИаН аИаЗ аМаНаОаЖаИбаЕаЛаЕаЙ т аНбаЛаЕаВаОаЙ аВаЕаКбаОб) ббаИбаАаЕббб баАаВаНбаМ аНбаЛаЕаВаОаМб аВаЕаКбаОбб.
аЂаАаКаИаМ аОаБбаАаЗаОаМ, аДаЛб аОаПбаЕаДаЕаЛаЕаНаИб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ аНаЕаОаБб
аОаДаИаМаО аЗаАаДаАбб аОбаИаЕаНбаАбаИб аПбаОбббаАаНббаВаА, баО аЕббб баКаАаЗаАбб, аКаАаКаАб ббаОаЙаКаА аВаЕаКбаОбаОаВ баВаЛбаЕббб аПбаАаВаОаЙ, аА аКаАаКаАб т аЛаЕаВаОаЙ. абаИ ббаОаМ аНаЕ баВаЛбаЕббб аОаБбаЗаАбаЕаЛбаНбаМ аЗаАаДаАаНаИаЕ аВ баАббаМаАббаИаВаАаЕаМаОаМ аПбаОбббаАаНббаВаЕ аКаАаКаОаЙ-аЛаИаБаО баИббаЕаМб аКаОаОбаДаИаНаАб. а баАббаНаОббаИ, аПбаИ аЗаАаДаАаНаНаОаЙ аОбаИаЕаНбаАбаИаИ аПбаОбббаАаНббаВаА баЕаЗбаЛббаАб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аНаЕ аЗаАаВаИбаИб аОб баОаГаО, баВаЛбаЕббб аЛаИ баАббаМаАббаИаВаАаЕаМаАб баИббаЕаМаА аКаОаОбаДаИаНаАб аПбаАаВаОаЙ аИаЛаИ аЛаЕаВаОаЙ. абаИ ббаОаМ баОбаМбаЛб аВббаАаЖаЕаНаИб аКаОаОбаДаИаНаАб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб баЕбаЕаЗ аКаОаОбаДаИаНаАбб аИбб
аОаДаНбб
аВаЕаКбаОбаОаВ аВ аПбаАаВаОаЙ аИ аЛаЕаВаОаЙ аОббаОаНаОбаМаИбаОаВаАаНаНаОаЙ аПббаМаОбаГаОаЛбаНаОаЙ баИббаЕаМаЕ аКаОаОбаДаИаНаАб аОбаЛаИбаАбббб аЗаНаАаКаОаМ.
ааЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аНаЕ аОаБаЛаАаДаАаЕб баВаОаЙббаВаАаМаИ аКаОаМаМббаАбаИаВаНаОббаИ аИ аАббаОбаИаАбаИаВаНаОббаИ. ааНаО баВаЛбаЕббб аАаНбаИаКаОаМаМббаАбаИаВаНбаМ аИ, аВ аОбаЛаИбаИаЕ аОб баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВ, баЕаЗбаЛббаАб баВаЛбаЕббб аОаПббб аВаЕаКбаОбаОаМ.
ааОаЛаЕаЗаНаО аДаЛб ТЋаИаЗаМаЕбаЕаНаИбТЛ аПаЕбаПаЕаНаДаИаКбаЛббаНаОббаИ аВаЕаКбаОбаОаВ т аМаОаДбаЛб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ баАаВаЕаН аПбаОаИаЗаВаЕаДаЕаНаИб аИб
аМаОаДбаЛаЕаЙ, аЕбаЛаИ аОаНаИ аПаЕбаПаЕаНаДаИаКбаЛббаНб, аИ баМаЕаНббаАаЕббб аДаО аНбаЛб, аЕбаЛаИ аВаЕаКбаОбб аКаОаЛаЛаИаНаЕаАбаНб.
аЈаИбаОаКаО аИбаПаОаЛбаЗбаЕббб аВаО аМаНаОаГаИб
баЕб
аНаИбаЕбаКаИб
аИ баИаЗаИбаЕбаКаИб
аПбаИаЛаОаЖаЕаНаИбб
. ааАаПбаИаМаЕб, аМаОаМаЕаНб аИаМаПбаЛббаА аИ баИаЛаА ааОбаЕаНбаА аМаАбаЕаМаАбаИбаЕбаКаИ аЗаАаПаИббаВаАбббб аВ аВаИаДаЕ аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб.
аЁаВаОаЙббаВаА
ааЕаОаМаЕббаИбаЕбаКаИаЕ баВаОаЙббаВаА аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
 а аИббаНаОаК 1: ааЛаОбаАаДб аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА баАаВаНаА аМаОаДбаЛб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб а аИббаНаОаК 1: ааЛаОбаАаДб аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА баАаВаНаА аМаОаДбаЛб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
 а аИббаНаОаК 2: ааБббаМ аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаДаА аПбаИ аИбаПаОаЛбаЗаОаВаАаНаИаИ аВаЕаКбаОбаНаОаГаО аИ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВ; аПбаНаКбаИбаНбаЕ аЛаИаНаИаИ аПаОаКаАаЗбаВаАбб аПбаОаЕаКбаИаИ аВаЕаКбаОбаА c аНаА a У b аИ аВаЕаКбаОбаА b У c аНаА a, аПаЕбаВбаМ баАаГаОаМ баВаЛбаЕббб аНаАб
аОаЖаДаЕаНаИаЕ аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб (аМаОаДбаЛб аКаОбаОбаОаГаО баАаВаЕаН аПаЛаОбаАаДаИ аОаДаНаОаЙ аИаЗ ббаОбаОаН), аА аВбаОббаМ т аНаАб
аОаЖаДаЕаНаИаЕ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб (аКаОбаОбаОаЕ баАаВаНаО аОаБббаМб аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаДаА) а аИббаНаОаК 2: ааБббаМ аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаДаА аПбаИ аИбаПаОаЛбаЗаОаВаАаНаИаИ аВаЕаКбаОбаНаОаГаО аИ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВ; аПбаНаКбаИбаНбаЕ аЛаИаНаИаИ аПаОаКаАаЗбаВаАбб аПбаОаЕаКбаИаИ аВаЕаКбаОбаА c аНаА a У b аИ аВаЕаКбаОбаА b У c аНаА a, аПаЕбаВбаМ баАаГаОаМ баВаЛбаЕббб аНаАб
аОаЖаДаЕаНаИаЕ аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб (аМаОаДбаЛб аКаОбаОбаОаГаО баАаВаЕаН аПаЛаОбаАаДаИ аОаДаНаОаЙ аИаЗ ббаОбаОаН), аА аВбаОббаМ т аНаАб
аОаЖаДаЕаНаИаЕ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб (аКаОбаОбаОаЕ баАаВаНаО аОаБббаМб аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаДаА)
- ааЕаОаБб
аОаДаИаМбаМ аИ аДаОббаАбаОбаНбаМ ббаЛаОаВаИаЕаМ аКаОаЛаЛаИаНаЕаАбаНаОббаИ аДаВбб
аНаЕаНбаЛаЕаВбб
аВаЕаКбаОбаОаВ баВаЛбаЕббб баАаВаЕаНббаВаО аНбаЛб аИб
аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб.
- ааОаДбаЛб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
![{\displaystyle [{\vec {a}},\;{\vec {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fcceaa8d6f8c20cebf7ca9374dc08a23130ba6a) баАаВаНбаЕббб аПаЛаОбаАаДаИ баАаВаНбаЕббб аПаЛаОбаАаДаИ  аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА, аПаОбббаОаЕаНаНаОаГаО аНаА аПбаИаВаЕаДбаНаНбб
аК аОаБбаЕаМб аНаАбаАаЛб аВаЕаКбаОбаАб аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА, аПаОбббаОаЕаНаНаОаГаО аНаА аПбаИаВаЕаДбаНаНбб
аК аОаБбаЕаМб аНаАбаАаЛб аВаЕаКбаОбаАб
 аИ аИ  (баМ. а аИббаНаОаК 1). (баМ. а аИббаНаОаК 1).
- абаЛаИ
 т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аОббаОаГаОаНаАаЛбаНбаЙ аВаЕаКбаОбаАаМ т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аОббаОаГаОаНаАаЛбаНбаЙ аВаЕаКбаОбаАаМ  аИ аИ  аИ аВбаБбаАаНаНбаЙ баАаК, ббаО ббаОаЙаКаА аИ аВбаБбаАаНаНбаЙ баАаК, ббаО ббаОаЙаКаА  т аПбаАаВаАб, аА т аПбаАаВаАб, аА  т аПаЛаОбаАаДб аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА, аПаОбббаОаЕаНаНаОаГаО аНаА аНаИб
(аПбаИаВаЕаДбаНаНбб
аК аОаБбаЕаМб аНаАбаАаЛб), баО аДаЛб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб баПбаАаВаЕаДаЛаИаВаА баОбаМбаЛаА: т аПаЛаОбаАаДб аПаАбаАаЛаЛаЕаЛаОаГбаАаМаМаА, аПаОбббаОаЕаНаНаОаГаО аНаА аНаИб
(аПбаИаВаЕаДбаНаНбб
аК аОаБбаЕаМб аНаАбаАаЛб), баО аДаЛб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб баПбаАаВаЕаДаЛаИаВаА баОбаМбаЛаА:
![{\displaystyle [{\vec {a}},\;{\vec {b}}]=S\cdot {\vec {e}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/659fe55fa7f1bfab81949bac7f9b6f460757c681)
- абаЛаИ
 т аКаАаКаОаЙ-аНаИаБбаДб аВаЕаКбаОб, т аКаАаКаОаЙ-аНаИаБбаДб аВаЕаКбаОб,  т аЛбаБаАб аПаЛаОбаКаОббб, баОаДаЕбаЖаАбаАб ббаОб аВаЕаКбаОб, т аЛбаБаАб аПаЛаОбаКаОббб, баОаДаЕбаЖаАбаАб ббаОб аВаЕаКбаОб,  т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аЛаЕаЖаАбаИаЙ аВ аПаЛаОбаКаОббаИ т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аЛаЕаЖаАбаИаЙ аВ аПаЛаОбаКаОббаИ  аИ аОббаОаГаОаНаАаЛбаНбаЙ аК аИ аОббаОаГаОаНаАаЛбаНбаЙ аК  , ,  т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аОббаОаГаОаНаАаЛбаНбаЙ аК аПаЛаОбаКаОббаИ т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аОббаОаГаОаНаАаЛбаНбаЙ аК аПаЛаОбаКаОббаИ  аИ аНаАаПбаАаВаЛаЕаНаНбаЙ баАаК, ббаО ббаОаЙаКаА аВаЕаКбаОбаОаВ аИ аНаАаПбаАаВаЛаЕаНаНбаЙ баАаК, ббаО ббаОаЙаКаА аВаЕаКбаОбаОаВ  баВаЛбаЕббб аПбаАаВаОаЙ, баО аДаЛб аЛбаБаОаГаО аЛаЕаЖаАбаЕаГаО аВ аПаЛаОбаКаОббаИ баВаЛбаЕббб аПбаАаВаОаЙ, баО аДаЛб аЛбаБаОаГаО аЛаЕаЖаАбаЕаГаО аВ аПаЛаОбаКаОббаИ  аВаЕаКбаОбаА аВаЕаКбаОбаА  баПбаАаВаЕаДаЛаИаВаА баОбаМбаЛаА баПбаАаВаЕаДаЛаИаВаА баОбаМбаЛаА
![{\displaystyle [{\vec {a}},\;{\vec {c}}]=\mathrm {Pr} _{\vec {e}}{\vec {a}}\cdot |{\vec {c}}|\cdot {\vec {g}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26453e25f5aa1dc2dad2f1ed1f24b394eded9bb5)
- абаИ аИбаПаОаЛбаЗаОаВаАаНаИаИ аВаЕаКбаОбаНаОаГаО аИ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИаЙ аМаОаЖаНаО аВбббаИбаАбб аОаБббаМ аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаДаА, аПаОбббаОаЕаНаНаОаГаО аНаА аПбаИаВаЕаДбаНаНбб
аК аОаБбаЕаМб аНаАбаАаЛб аВаЕаКбаОбаАб
a, b аИ c (баМ. а аИббаНаОаК 2). аЂаАаКаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ ббаЕб
аВаЕаКбаОбаОаВ аНаАаЗбаВаАаЕббб баМаЕбаАаНаНбаМ.
![{\displaystyle V=|\langle {\vec {a}},\;[{\vec {b}},\;{\vec {c}}]\rangle |.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/972d8b2c2701aa4ae5182148ac7c6cb92a0d3413)
ааА баИббаНаКаЕ аПаОаКаАаЗаАаНаО, ббаО ббаОб аОаБббаМ аМаОаЖаЕб аБббб аНаАаЙаДаЕаН аДаВбаМб баПаОбаОаБаАаМаИ: аГаЕаОаМаЕббаИбаЕбаКаИаЙ баЕаЗбаЛббаАб баОб
баАаНбаЕббб аДаАаЖаЕ аПбаИ аЗаАаМаЕаНаЕ ТЋбаКаАаЛббаНаОаГаОТЛ аИ ТЋаВаЕаКбаОбаНаОаГаОТЛ аПбаОаИаЗаВаЕаДаЕаНаИаЙ аМаЕббаАаМаИ:
![{\displaystyle V=\langle [{\vec {a}},\;{\vec {b}}],\;{\vec {c}}\rangle =\langle {\vec {a}},\;[{\vec {b}},\;{\vec {c}}]\rangle .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4ba1da1621205def6e3ddee53ed9da404935595)
ааЕаЛаИбаИаНаА аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аЗаАаВаИбаИб аОб баИаНббаА баГаЛаА аМаЕаЖаДб аИаЗаНаАбаАаЛбаНбаМаИ аВаЕаКбаОбаАаМаИ, аПаОббаОаМб аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аМаОаЖаЕб аВаОбаПбаИаНаИаМаАбббб аКаАаК ббаЕаПаЕаНб ТЋаПаЕбаПаЕаНаДаИаКбаЛббаНаОббаИТЛ аВаЕаКбаОбаОаВ баАаК аЖаЕ, аКаАаК аИ баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аМаОаЖаЕб баАббаМаАббаИаВаАбббб аКаАаК ббаЕаПаЕаНб ТЋаПаАбаАаЛаЛаЕаЛбаНаОббаИТЛ. ааЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аДаВбб
аЕаДаИаНаИбаНбб
аВаЕаКбаОбаОаВ баАаВаНаО 1 (аЕаДаИаНаИбаНаОаМб аВаЕаКбаОбб), аЕбаЛаИ аИаЗаНаАбаАаЛбаНбаЕ аВаЕаКбаОбб аПаЕбаПаЕаНаДаИаКбаЛббаНб, аИ баАаВаНаО 0 (аНбаЛаЕаВаОаМб аВаЕаКбаОбб), аЕбаЛаИ аВаЕаКбаОбб аПаАбаАаЛаЛаЕаЛбаНб аЛаИаБаО аАаНбаИаПаАбаАаЛаЛаЕаЛбаНб.
ааЛаГаЕаБбаАаИбаЕбаКаИаЕ баВаОаЙббаВаА аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
ааАаЛаЕаЕ ![{\displaystyle [{\vec {a}},\;{\vec {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fcceaa8d6f8c20cebf7ca9374dc08a23130ba6a) аИ аИ  аОаБаОаЗаНаАбаАбб баОаОбаВаЕбббаВаЕаНаНаО аВаЕаКбаОбаНаОаЕ аИ баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аОаБаОаЗаНаАбаАбб баОаОбаВаЕбббаВаЕаНаНаО аВаЕаКбаОбаНаОаЕ аИ баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ  аИ аИ  . .
| абаЕаДббаАаВаЛаЕаНаИаЕ
|
ааПаИбаАаНаИаЕ
|
![{\displaystyle [{\vec {a}},\;{\vec {b}}]=-[{\vec {b}},{\vec {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c267366cadb584259b3c50b0e4e36382c5f9e9bd)
|
ааНбаИаКаОаМаМббаАбаИаВаНаОббб.
|
![{\displaystyle [\alpha \cdot {\vec {a}},\;{\vec {b}}]=[{\vec {a}},\;\alpha \cdot {\vec {b}}]=\alpha \cdot [{\vec {a}},\;{\vec {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b268a3e418241b2c2fc88d8472c2a2e1566f356)
|
аббаОбаИаАбаИаВаНаОббб баМаНаОаЖаЕаНаИб аНаА баКаАаЛбб.
|
![{\displaystyle [{\vec {a}}+{\vec {b}},\;{\vec {c}}]=[{\vec {a}},\;{\vec {c}}]+[{\vec {b}},\;{\vec {c}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3161075b7aad486d9877967a12eb2d725bca5d3)
|
ааИбббаИаБббаИаВаНаОббб аПаО баЛаОаЖаЕаНаИб.
|
![{\displaystyle [[{\vec {a}},\;{\vec {b}}],\;{\vec {c}}]+[[{\vec {b}},\;{\vec {c}}],\;{\vec {a}}]+[[{\vec {c}},{\vec {a}}],\;{\vec {b}}]={\vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00f9fa2cabab740204011537035a86bb96df0a3b)
|
аЂаОаЖаДаЕббаВаО аЏаКаОаБаИ.
|
![{\displaystyle [{\vec {a}},\;{\vec {a}}]={\vec {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2b6acb122bbc38e8a68353a2a7230885ff4d8c5)
|
|
![{\displaystyle [{\vec {a}},\;[{\vec {b}},\;{\vec {c}}]]={\vec {b}}\cdot \langle {\vec {a}},\;{\vec {c}}\rangle -{\vec {c}}\cdot \langle {\vec {a}},\;{\vec {b}}\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7b7dbf2d84c0db27feb86c85c41b7d122646f07)
|
аЄаОбаМбаЛаА ТЋаааІ аМаИаНбб аІааТЛ, баОаЖаДаЕббаВаО ааАаГбаАаНаЖаА.
|
![{\displaystyle |[{\vec {a}},\,{\vec {b}}]|^{2}+\langle {\vec {a}},\,{\vec {b}}\rangle ^{2}=|{\vec {a}}|^{2}\cdot |{\vec {b}}|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff5696724e36f03030ef3350e333494d1d774ec)
|
аЇаАббаНбаЙ баЛббаАаЙ аМбаЛббаИаПаЛаИаКаАбаИаВаНаОббаИ аНаОбаМб аКаВаАбаЕбаНаИаОаНаОаВ.
|
![{\displaystyle \langle [{\vec {a}},\,{\vec {b}}],\,{\vec {c}}\rangle =\langle {\vec {a}},\,[{\vec {b}},\,{\vec {c}}]\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5b749162f3b3230fc7193d64f2f3910b791bcc9)
|
ааНаАбаЕаНаИаЕ ббаОаГаО аВббаАаЖаЕаНаИб аНаАаЗбаВаАбб баМаЕбаАаНаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИаЕаМ аВаЕаКбаОбаОаВ  , ,  , ,  . .
|
ааДаИаНббаВаЕаНаНаОббб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб
абббаНаИаМ, аНаАбаКаОаЛбаКаО аНаЕаОаБб
аОаДаИаМаО ббаАаНаДаАббаНаОаЕ аОаПбаЕаДаЕаЛаЕаНаИаЕ аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб. абаИббаМ ббаО ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аДаОаЛаЖаНаО аОбаВаЕбаАбб баЕаМ ббаЛаОаВаИбаМ, аКаОбаОббаЕ аДаЕаЛаАбб аВаОаЗаМаОаЖаНбаМ баПаОббаЕаБаЛаЕаНаИаЕ баАаМаОаГаО баЕбаМаИаНаА ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ[33].
абббб аНаЕаКаОбаОбаАб аОаПаЕбаАбаИб  ббаАаВаИб аВ баОаОбаВаЕбббаВаИаЕ аДаВбаМ аВаЕаКбаОбаАаМ ббаАаВаИб аВ баОаОбаВаЕбббаВаИаЕ аДаВбаМ аВаЕаКбаОбаАаМ  аИ аИ  ббаЕбаИаЙ аВаЕаКбаОб ббаЕбаИаЙ аВаЕаКбаОб  . а аПбббб ббаА аОаПаЕбаАбаИб аОаБаЛаАаДаАаЕб[33]: . а аПбббб ббаА аОаПаЕбаАбаИб аОаБаЛаАаДаАаЕб[33]:
- аАббаОбаИаАбаИаВаНаОбббб аПбаИ баМаНаОаЖаЕаНаИаИ аВаЕаКбаОбаА аНаА баИбаЛаО
 ; ;
- аДаИбббаИаБббаИаВаНаОбббб
 ; ;
- аГаЕаОаМаЕббаИбаЕбаКаИаМ баМббаЛаОаМ, баО аЕббб аЕбаЛаИ аВаЕаКбаОбб
 аИ аИ  аОбаОаБбаАаЖаАбббб аВ аВаЕаКбаОбб аОбаОаБбаАаЖаАбббб аВ аВаЕаКбаОбб  аИ аИ  аЛбаБбаМ аДаВаИаЖаЕаНаИаЕаМ аПбаОбббаАаНббаВаА (аНаАаПбаИаМаЕб, аВбаАбаЕаНаИаЕаМ аВаОаКббаГ баОбаКаИ аЛбаБбаМ аДаВаИаЖаЕаНаИаЕаМ аПбаОбббаАаНббаВаА (аНаАаПбаИаМаЕб, аВбаАбаЕаНаИаЕаМ аВаОаКббаГ баОбаКаИ  ), баО баОаГаДаА аИ аВаЕаКбаОб ), баО баОаГаДаА аИ аВаЕаКбаОб  аПбаИ ббаОаМ аДаВаИаЖаЕаНаИаИ баАаКаЖаЕ аОбаОаБбаАаЖаАаЕббб аВ аВаЕаКбаОб аПбаИ ббаОаМ аДаВаИаЖаЕаНаИаИ баАаКаЖаЕ аОбаОаБбаАаЖаАаЕббб аВ аВаЕаКбаОб  . .
аЂаЕаОбаЕаМаА. ааДаИаНббаВаЕаНаНаОббб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб. ааПбаЕаДаЕаЛбаНаНаОаЕ аВббаЕ ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аВаЕаКбаОбаОаВ  аЕббб аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аЕббб аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) [33]. [33].
ааОаКаАаЗаАбаЕаЛбббаВаО [22]
ааОаКаАаЗаАбаЕаЛбббаВаО аПаОаДаОаБаНаО аДаОаКаАаЗаАбаЕаЛбббаВб баЕаОбаЕаМб аО аЕаДаИаНббаВаЕаНаНаОббаИ баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВ бббб
аМаЕбаНаОаМ аПбаОбббаАаНббаВаЕ[22].
1. ааЕбаЕб
аОаД аК аЕаДаИаНаИбаНбаМ аВаЕаКбаОбаАаМ. абббб аПбаОаИаЗаВаОаЛбаНбаЕ аВаЕаКбаОбб  , ,  , аГаДаЕ , аГаДаЕ  аИ аИ  т аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб. аЂаОаГаДаА, аПаО баВаОаЙббаВб аАббаОбаИаАбаИаВаНаОббаИ ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ, т аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб. аЂаОаГаДаА, аПаО баВаОаЙббаВб аАббаОбаИаАбаИаВаНаОббаИ ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ,
 , ,
баО аЕббб аДаОббаАбаОбаНаО аЗаАаДаАбб ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аПбаОаИаЗаВаОаЛбаНбб
аЕаДаИаНаИбаНбб
аВаЕаКбаОбаОаВ  аИ аИ  [33]. [33].
 ааЕбаПаЕаНаДаИаКбаЛбб аК аЕаДаИаНаИбаНбаМ аВаЕаКбаОбаАаМ ааЕбаПаЕаНаДаИаКбаЛбб аК аЕаДаИаНаИбаНбаМ аВаЕаКбаОбаАаМ
2. ааЕбаПаЕаНаДаИаКбаЛббаНаОббб ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ аВаЕаКбаОбаАаМ  аИ аИ  . абаОаВаЕаДбаМ аК аПаЛаОбаКаОббаИ аЕаДаИаНаИбаНбб
аВаЕаКбаОбаОаВ . абаОаВаЕаДбаМ аК аПаЛаОбаКаОббаИ аЕаДаИаНаИбаНбб
аВаЕаКбаОбаОаВ  аИ аИ  аПаЕбаПаЕаНаДаИаКбаЛббаНбб аПббаМбб аПаЕбаПаЕаНаДаИаКбаЛббаНбб аПббаМбб  (баМ. баИббаНаОаК баПбаАаВаА б аПаЛаОбаКаОбббб аИ аПаЕбаПаЕаНаДаИаКбаЛббаНаОаЙ аПббаМаОаЙ)[34]. (баМ. баИббаНаОаК баПбаАаВаА б аПаЛаОбаКаОбббб аИ аПаЕбаПаЕаНаДаИаКбаЛббаНаОаЙ аПббаМаОаЙ)[34].
абаЛаИ аПаОаВаЕбаНббб ббб аПаЛаОбаКаОббб аОбаНаОбаИбаЕаЛбаНаО аПббаМаОаЙ  аНаА аНаА  , баО аВаЕаКбаОбб , баО аВаЕаКбаОбб  аИ аИ  аОбаОаБбаАаЗбббб аВ аВаЕаКбаОбб аОбаОаБбаАаЗбббб аВ аВаЕаКбаОбб  аИ аИ  баОаОбаВаЕбббаВаЕаНаНаО. ааОббаОаМб ббаОб аПаОаВаОбаОб аДаОаЛаЖаЕаН аОбаОаБбаАаЗаИбб ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аВаЕаКбаОбаОаВ баОаОбаВаЕбббаВаЕаНаНаО. ааОббаОаМб ббаОб аПаОаВаОбаОб аДаОаЛаЖаЕаН аОбаОаБбаАаЗаИбб ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аВаЕаКбаОбаОаВ  аВ ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аВаЕаКбаОбаОаВ аВ ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аВаЕаКбаОбаОаВ

аПаО баВаОаЙббаВб аАббаОбаИаАбаИаВаНаОббаИ ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ, аДббаГаИаМаИ баЛаОаВаАаМаИ, аОббаАаВаИбб аВаЕаКбаОб  аНаА аМаЕббаЕ. абаО аВаОаЗаМаОаЖаНаО баОаЛбаКаО баОаГаДаА, аКаОаГаДаА аВаЕаКбаОб аНаА аМаЕббаЕ. абаО аВаОаЗаМаОаЖаНаО баОаЛбаКаО баОаГаДаА, аКаОаГаДаА аВаЕаКбаОб  аЛаЕаЖаИб аНаА аПббаМаОаЙ аЛаЕаЖаИб аНаА аПббаМаОаЙ  , аДббаГаИаМаИ баЛаОаВаАаМаИ, аПаЕбаПаЕаНаДаИаКбаЛббаЕаН аВаЕаКбаОбаАаМ , аДббаГаИаМаИ баЛаОаВаАаМаИ, аПаЕбаПаЕаНаДаИаКбаЛббаЕаН аВаЕаКбаОбаАаМ  аИ аИ  [34]. [34].
3. ТЋааВаАаДбаАбТЛ аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА. ааЛб аЛбаБаОаГаО аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА  аЕаГаО ТЋаКаВаАаДбаАбТЛ аЕаГаО ТЋаКаВаАаДбаАбТЛ  баАаВаЕаН аНбаЛб-аВаЕаКбаОбб баАаВаЕаН аНбаЛб-аВаЕаКбаОбб  [34]: [34]:
 . .
ааЕаЙббаВаИбаЕаЛбаНаО, аКаОаГаДаА аВ ТЋаПбаОаИаЗаВаЕаДаЕаНаИаИТЛ  аВаЕаКбаОб аВаЕаКбаОб  баОаВаПаАаДаАаЕб б аВаЕаКбаОбаОаМ баОаВаПаАаДаАаЕб б аВаЕаКбаОбаОаМ  , баО аВаЕаКбаОб , баО аВаЕаКбаОб  аПбаИаНаАаДаЛаЕаЖаИб аБаЕббаИбаЛаЕаНаНаОаМб аКаОаЛаИбаЕббаВб аПббаМбб аПбаИаНаАаДаЛаЕаЖаИб аБаЕббаИбаЛаЕаНаНаОаМб аКаОаЛаИбаЕббаВб аПббаМбб
 , аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аВаЕаКбаОбб , аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аВаЕаКбаОбб  , аА баАаКаОаЕ аВаОаЗаМаОаЖаНаО баОаЛбаКаО б аНбаЛаЕаВбаМ аВаЕаКбаОбаОаМ[34]. , аА баАаКаОаЕ аВаОаЗаМаОаЖаНаО баОаЛбаКаО б аНбаЛаЕаВбаМ аВаЕаКбаОбаОаМ[34].
4. ТЋабаОаИаЗаВаЕаДаЕаНаИаЕТЛ аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аВаЕаКбаОбаОаВ. а аАббаМаОббаИаМ аВаЕаКбаОб  баАаКаОаЙ, ббаО баАаКаОаЙ, ббаО  . ааЛб аНаЕаГаО ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аВаЕаКбаОбаОаВ . ааЛб аНаЕаГаО ТЋаПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ аВаЕаКбаОбаОаВ
 , ,
аГаДаЕ  т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аПаЕбаПаЕаНаДаИаКбаЛббаНбаЙ аВаЕаКбаОбаАаМ т аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аПаЕбаПаЕаНаДаИаКбаЛббаНбаЙ аВаЕаКбаОбаАаМ  аИ аИ  . абббб, аДаЛб аОаДаНаОаЗаНаАбаНаОббаИ, аВаЕаКбаОб . абббб, аДаЛб аОаДаНаОаЗаНаАбаНаОббаИ, аВаЕаКбаОб  баАаКаОаЙ, ббаО б аЕаГаО аКаОаНбаА аПаОаВаОбаОб аНаА баАаКаОаЙ, ббаО б аЕаГаО аКаОаНбаА аПаОаВаОбаОб аНаА  аОб аВаЕаКбаОбаА аОб аВаЕаКбаОбаА  аК аВаЕаКбаОбб аК аВаЕаКбаОбб  аВаИаДаЕаЛбб аПбаОбаИаВ баАбаОаВаОаЙ бббаЕаЛаКаИ[34]. аВаИаДаЕаЛбб аПбаОбаИаВ баАбаОаВаОаЙ бббаЕаЛаКаИ[34].
5. ааОббаОбаНббаВаО аМаНаОаЖаИбаЕаЛб  . ааОаКаАаЖаЕаМ, ббаО аМаНаОаЖаИбаЕаЛб . ааОаКаАаЖаЕаМ, ббаО аМаНаОаЖаИбаЕаЛб  аПаОббаОбаНаЕаН, баО аЕббб аПаОаКаАаЖаЕаМ, ббаО аОаН аОаДаИаНаАаКаОаВ аДаЛб аПбаОаИаЗаВаОаЛбаНбб
аДаВбб
аВаЗаАаИаМаНаО аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аЕаДаИаНаИбаНбб
аВаЕаКбаОбаОаВ аПаОббаОбаНаЕаН, баО аЕббб аПаОаКаАаЖаЕаМ, ббаО аОаН аОаДаИаНаАаКаОаВ аДаЛб аПбаОаИаЗаВаОаЛбаНбб
аДаВбб
аВаЗаАаИаМаНаО аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аЕаДаИаНаИбаНбб
аВаЕаКбаОбаОаВ  аИ аИ  . ааЕаЙббаВаИбаЕаЛбаНаО, аПбббб . ааЕаЙббаВаИбаЕаЛбаНаО, аПбббб  аИ аИ  т аПаАбаА аДббаГаИб
аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аЕаДаИаНаИбаНбб
аВаЕаКбаОбаА. аЂаОаГаДаА аПаОаВаОбаОб аПаЛаОбаКаОббаИ, аКаОбаОббаЙ аПаЕбаЕаВаОаДаИб аВаЕаКбаОбб т аПаАбаА аДббаГаИб
аПаЕбаПаЕаНаДаИаКбаЛббаНбб
аЕаДаИаНаИбаНбб
аВаЕаКбаОбаА. аЂаОаГаДаА аПаОаВаОбаОб аПаЛаОбаКаОббаИ, аКаОбаОббаЙ аПаЕбаЕаВаОаДаИб аВаЕаКбаОбб  аИ аИ  баОаОбаВаЕбббаВаЕаНаНаО аВ аВаЕаКбаОбб баОаОбаВаЕбббаВаЕаНаНаО аВ аВаЕаКбаОбб  аИ аИ  , аОбаОаБбаАаЖаАаЕб аВаЕаКбаОб , аОбаОаБбаАаЖаАаЕб аВаЕаКбаОб  аВ аВаЕаКбаОб аВ аВаЕаКбаОб  . ааДаЕбб баЕбаЕаЗ . ааДаЕбб баЕбаЕаЗ  аОаБаОаЗаНаАбаЕаН аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аКаОбаОббаЙ аОаПбаЕаДаЕаЛбаН аВаЕаКбаОбаАаМаИ аОаБаОаЗаНаАбаЕаН аЕаДаИаНаИбаНбаЙ аВаЕаКбаОб, аКаОбаОббаЙ аОаПбаЕаДаЕаЛбаН аВаЕаКбаОбаАаМаИ  аИ аИ  баОбаНаО баАаК аЖаЕ, аКаАаК аПаОаЛббаИаЛбб аВаЕаКбаОб баОбаНаО баАаК аЖаЕ, аКаАаК аПаОаЛббаИаЛбб аВаЕаКбаОб  аИаЗ аВаЕаКбаОбаОаВ аИаЗ аВаЕаКбаОбаОаВ  аИ аИ  . а аИбаОаГаЕ аПаОаЛббаАаЕаМ[34]: . а аИбаОаГаЕ аПаОаЛббаАаЕаМ[34]:
  . .
 абаОаЕаКбаИаИ аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА аНаА аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб абаОаЕаКбаИаИ аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА аНаА аЕаДаИаНаИбаНбаЕ аВаЕаКбаОбб
6. ааДаИаНббаВаЕаНаНаОббб аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб. ааОбаЛаЕаДаНаИаЙ баАаГ баОббаОаИб аВ баАаЗаЛаОаЖаЕаНаИаИ аПбаОаИаЗаВаОаЛбаНаОаГаО аЕаДаИаНаИбаНаОаГаО аВаЕаКбаОбаА  аПаО аПаЕбаПаЕаНаДаИаКбаЛббаНбаМ аЕаДаИаНаИбаНбаМ аВаЕаКбаОбаАаМ аПаО аПаЕбаПаЕаНаДаИаКбаЛббаНбаМ аЕаДаИаНаИбаНбаМ аВаЕаКбаОбаАаМ  аИ аИ  , аПбаИббаМ аВаЕаКбаОб , аПбаИббаМ аВаЕаКбаОб  аПбаИаНаАаДаЛаЕаЖаИб аПаЛаОбаКаОббаИ аВаЕаКбаОбаОаВ аПбаИаНаАаДаЛаЕаЖаИб аПаЛаОбаКаОббаИ аВаЕаКбаОбаОаВ  аИ аИ  , аИ аПбббб баГаОаЛ аМаЕаЖаДб аЕаДаИаНаИбаНбаМаИ аВаЕаКбаОбаАаМаИ , аИ аПбббб баГаОаЛ аМаЕаЖаДб аЕаДаИаНаИбаНбаМаИ аВаЕаКбаОбаАаМаИ  аИ аИ  баАаВаЕаН баАаВаЕаН  (баМ. баИббаНаОаК баПбаАаВаА б аПбаОаЕаКбаИбаМаИ аВаЕаКбаОбаА (баМ. баИббаНаОаК баПбаАаВаА б аПбаОаЕаКбаИбаМаИ аВаЕаКбаОбаА  ). аЂаОаГаДаА аПаОаЛббаИаМ[34]: ). аЂаОаГаДаА аПаОаЛббаИаМ[34]:

абаПаОаЛбаЗбаЕаМ аВ аВбаКаЛаАаДаКаАб
баЛаЕаДбббаИаЕ баАаВаЕаНббаВаА:
- аДаИбббаИаБббаИаВаНаОббб ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ,
- аАббаОбаИаАбаИаВаНаОббб ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ аПбаИ баМаНаОаЖаЕаНаИаИ аВаЕаКбаОбаА аНаА баИбаЛаО,
 , ,  , ,
баЛаЕаДаОаВаАбаЕаЛбаНаО[34]:

ааЗ аПаОбаЛаЕаДаНаЕаГаО баАаВаЕаНббаВаА аОаКаОаНбаАбаЕаЛбаНаО аПаОаЛббаАаЕаМ:
![{\displaystyle \mathbf {a} *\mathbf {b} =\lambda |\mathbf {a} ||\mathbf {b} |\sin \theta \cdot u^{0}=\lambda [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7efbb50c652bbad9e5385e7383d39050e7bf2397)
аГаДаЕ  [34]. [34].
ааАаМаЕбаАаНаИаЕ. абаАаК, аПбаИ аИбаПаОаЛбаЗаОаВаАаНаИаИ баЛаЕаДбббаИб
ббаЕаБаОаВаАаНаИаЙ ТЋаВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИбТЛ  : :
- аАббаОбаИаАбаИаВаНаОббаИ аПбаИ баМаНаОаЖаЕаНаИаИ аВаЕаКбаОбаА аНаА баИбаЛаО,
- аДаИбббаИаБббаИаВаНаОббаИ,
аПаОаЛббаАаЕббб аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ ![{\displaystyle [a,b].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ba5cb29655f824ce80a0b6a32d9326d0e8742cd) ааОббаОаМб, аЕбаЛаИ аДаОаПаОаЛаНаИбб ббаИ ббаАббаЕ ббаЕаБаОаВаАаНаИб аОаДаНаИаМ аИаЗ баЛаЕаДбббаИб
аНаОаВбб
ббаЕаБаОаВаАаНаИаЙ: ааОббаОаМб, аЕбаЛаИ аДаОаПаОаЛаНаИбб ббаИ ббаАббаЕ ббаЕаБаОаВаАаНаИб аОаДаНаИаМ аИаЗ баЛаЕаДбббаИб
аНаОаВбб
ббаЕаБаОаВаАаНаИаЙ:
- аКаОаМаМббаАбаИаВаНаОббаИ
 , ,
- аАббаОбаИаАбаИаВаНаОббаИ аВ аОаБббаНаОаМ баМббаЛаЕ
 , ,
аПаОаЛббаАаЕббб баОаЛбаКаО ТЋаНбаЛаЕаВаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕТЛ  (баОаВаЕббаЕаНаНаО аНаЕаИаНбаЕбаЕбаНаОаЕ). аЁаЛаЕаДаОаВаАбаЕаЛбаНаО, ббаАббаЕ ббаЕаБаОаВаАаНаИб аИ б
аОбб аБб аОаДаНаО аИаЗ аНаОаВбаЙ ббаЕаБаОаВаАаНаИаЙ аНаЕбаОаВаМаЕббаИаМб (аКаОаНаЕбаНаО, баОаЛбаКаО аПбаИ аГаЕаОаМаЕббаИбаЕбаКаОаМ баМббаЛаЕ ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ (баОаВаЕббаЕаНаНаО аНаЕаИаНбаЕбаЕбаНаОаЕ). аЁаЛаЕаДаОаВаАбаЕаЛбаНаО, ббаАббаЕ ббаЕаБаОаВаАаНаИб аИ б
аОбб аБб аОаДаНаО аИаЗ аНаОаВбаЙ ббаЕаБаОаВаАаНаИаЙ аНаЕбаОаВаМаЕббаИаМб (аКаОаНаЕбаНаО, баОаЛбаКаО аПбаИ аГаЕаОаМаЕббаИбаЕбаКаОаМ баМббаЛаЕ ТЋаПбаОаИаЗаВаЕаДаЕаНаИбТЛ  )[34]. )[34].
абаОаИаЗаВаЕаДаЕаНаИб бббб
аВаЕаКбаОбаОаВ
абаОббаЕаЙбаЕаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ бббб
аВаЕаКбаОбаОаВ
абаОббаЕЬаЙбаЕаЕ аПбаОаИаЗаВаЕаДаЕЬаНаИаЕ бббб
аВаЕаКбаОбаОЬаВ т баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аДаВбб
аВаЕаКбаОбаОаВ  , баМаНаОаЖаЕаНаНаОаЕ аНаА ббаЕбаИаЙ аВаЕаКбаОб , баМаНаОаЖаЕаНаНаОаЕ аНаА ббаЕбаИаЙ аВаЕаКбаОб  [7]: [7]:

абаОббаЕаЙбаЕаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ бббб
аВаЕаКбаОбаОаВ  т аВаЕаКбаОб, аКаОбаОббаЙ аКаОаЛаЛаИаНаЕаАбаЕаН аВаЕаКбаОбб аВаЕаКбаОб т аВаЕаКбаОб, аКаОбаОббаЙ аКаОаЛаЛаИаНаЕаАбаЕаН аВаЕаКбаОбб аВаЕаКбаОб  , баО аЕббб баОаМб баВаОаЕаМб аМаНаОаЖаИбаЕаЛб, аКаОбаОббаЙ аНаАб
аОаДаИббб аВаНаЕ аЗаНаАаКаА баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб[7]. , баО аЕббб баОаМб баВаОаЕаМб аМаНаОаЖаИбаЕаЛб, аКаОбаОббаЙ аНаАб
аОаДаИббб аВаНаЕ аЗаНаАаКаА баКаАаЛббаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб[7].
ааЗ ббаОаЙ аКаОаЛаЛаИаНаЕаАбаНаОббаИ баЛаЕаДбаЕб аНаЕбаАаВаЕаНббаВаО

аКаОбаОбаОаЕ аПбаЕаВбаАбаАаЕббб аВ баАаВаЕаНббаВаО баОаГаДаА аИ баОаЛбаКаО баОаГаДаА, аКаОаГаДаА аВаЕаКбаОбб  аИ аИ  аКаОаЛаЛаИаНаЕаАбаНб. аббаГаИаМаИ баЛаОаВаАаМаИ, аПбаОббаЕаЙбаЕаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ бббб
аВаЕаКбаОбаОаВ аНаЕ аАббаОбаИаАбаИаВаНаО[7]. аКаОаЛаЛаИаНаЕаАбаНб. аббаГаИаМаИ баЛаОаВаАаМаИ, аПбаОббаЕаЙбаЕаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ бббб
аВаЕаКбаОбаОаВ аНаЕ аАббаОбаИаАбаИаВаНаО[7].
ааВаОаЙаНаОаЕ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ
ааВаОаЙаНаОЬаЕ аВаЕЬаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕЬаНаИаЕ (аДббаГаИаЕ аНаАаЗаВаАаНаИб: ббаОаЙаНаОаЕ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ; аВаЕаКбаОбаНаО-аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ) ![{\displaystyle \left[{\vec {a}},{\vec {b}},{\vec {c}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5516ee4951b687c51ae4fdaf2bd2bfbb4f75d63) аВаЕаКбаОбаОаВ аВаЕаКбаОбаОаВ  т аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаА т аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаА  аНаА аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аНаА аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ  аИ аИ 
![{\displaystyle \left[{\vec {a}},{\vec {b}},{\vec {c}}\right]=\left[{\vec {a}},\left[{\vec {b}},{\vec {c}}\right]\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d25ec0ade11817559ae9c35a44c380117a2b764e)
а аЛаИбаЕбаАбббаЕ ббаОб баИаП аПбаОаИаЗаВаЕаДаЕаНаИб бббб
аВаЕаКбаОбаОаВ аНаАаЗбаВаАаЕббб аКаАаК ббаОаЙаНбаМ[35][36] (аПаО баИбаЛб аВаЕаКбаОбаОаВ, аОаБббаНаО аВ аАаНаГаЛаОбаЗббаНбб
аИ аПаЕбаЕаВаОаДаНбб
аИббаОбаНаИаКаАб
), баАаК аИ аДаВаОаЙаНбаМ[37][38][39][6], аИаЛаИ аВаЕаКбаОбаНаО-аВаЕаКбаОбаНбаМ[39] (аПаО баИбаЛб аОаПаЕбаАбаИаЙ баМаНаОаЖаЕаНаИб, аОаБббаНаО аВ аОбаИаГаИаНаАаЛбаНбб
ббббаКаОбаЗббаНбб
аИббаОбаНаИаКаАб
).
аЁаВаОаЙббаВаА
аЄаОбаМбаЛаА ааАаГбаАаНаЖаА
ааЛб аДаВаОаЙаНаОаГаО аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб баПбаАаВаЕаДаЛаИаВаА баОбаМбаЛаА ааАаГбаАаНаЖаА:
![{\displaystyle {\Big [}{\vec {a}},{\big [}{\vec {b}},{\vec {c}}{\big ]}{\Big ]}={\vec {a}}\times {\big (}{\vec {b}}\times {\vec {c}}{\big )}={\vec {b}}{\big (}{\vec {a}}\cdot {\vec {c}}{\big )}-{\vec {c}}{\big (}{\vec {a}}\cdot {\vec {b}}{\big )},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/786531cc83fa02005050f0996904731a272479ff)
аКаОбаОббб аМаОаЖаНаО аЗаАаПаОаМаНаИбб аПаО аМаНаЕаМаОаНаИбаЕбаКаОаМб аПбаАаВаИаЛб ТЋаБаАб аМаИаНбб баАаБТЛ.
ааОаКаАаЗаАбаЕаЛбббаВаО 1
абаБаЕбаЕаМ аПбаАаВбаЙ аОббаОаНаОбаМаИбаОаВаАаНаНбаЙ аБаАаЗаИб  баАаК, ббаОаБб баАаК, ббаОаБб
  
аЂаОаГаДаА
![{\displaystyle \left[{\vec {b}},{\vec {c}}\right]=\left(0,0,-\beta _{2}\gamma _{1}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/711d686f29d08b6c0f159c18cde16deafbd28417) ![{\displaystyle \left[{\vec {a}},\left[{\vec {b}},{\vec {c}}\right]\right]=\left(-\alpha _{2}\beta _{2}\gamma _{1},\alpha _{1}\beta _{2}\gamma _{1},0\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64275fc8b28ff088ed73518658feae05fb5dd992)
аИ

аЂаАаКаИаМ аОаБбаАаЗаОаМ,
![{\displaystyle \left[{\vec {a}},\left[{\vec {b}},{\vec {c}}\right]\right]={\vec {b}}\left({\vec {a}}\cdot {\vec {c}}\right)-{\vec {c}}\left({\vec {a}}\cdot {\vec {b}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76f8325b29e2087be9e09986648ce21d0031b72d)
аббаГаОаЙ аВаАбаИаАаНб аДаОаКаАаЗаАбаЕаЛбббаВаА аИбаПаОаЛбаЗбаЕб баАаЗаЛаОаЖаЕаНаИаЕ аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аПаО аКаОаМаПаОаНаЕаНбаАаМ б аПаОаМаОббб баЕаНаЗаОбаА ааЕаВаИ-аЇаИаВаИбб  : :
![{\displaystyle [{\vec {a}},\;{\vec {b}}]_{i}=\varepsilon _{ijk}a_{j}b_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0208d5e804d66cac8d217f91a88608e63326b3c)
(аЗаДаЕбб аИ аНаИаЖаЕ аПаО аПаОаВбаОббббаИаМбб аИаНаДаЕаКбаАаМ аПбаОаИаЗаВаОаДаИббб ббаМаМаИбаОаВаАаНаИаЕ, б.аЕ.  баМ. баОаГаЛаАбаЕаНаИаЕ ааЙаНббаЕаЙаНаА аО ббаМаМаИбаОаВаАаНаИаИ). баМ. баОаГаЛаАбаЕаНаИаЕ ааЙаНббаЕаЙаНаА аО ббаМаМаИбаОаВаАаНаИаИ).
![{\displaystyle \left[{\vec {a}},\left[{\vec {b}},{\vec {c}}\right]\right]_{i}=\varepsilon _{ijk}a_{j}(\varepsilon _{klm}b_{l}c_{m})=\varepsilon _{ijk}\varepsilon _{klm}a_{j}b_{l}c_{m}=(\delta _{il}\delta _{jm}-\delta _{im}\delta _{jl})a_{j}b_{l}c_{m}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b0b96f916403ac58e579afcfa4731e0937067ea)
абаПаОаЛбаЗаОаВаАаНаО баОаОбаНаОбаЕаНаИаЕ  аГаДаЕ аГаДаЕ  т баИаМаВаОаЛ абаОаНаЕаКаЕбаА. ааАаЛаЕаЕ, т баИаМаВаОаЛ абаОаНаЕаКаЕбаА. ааАаЛаЕаЕ,
![{\displaystyle \left[{\vec {a}},\left[{\vec {b}},{\vec {c}}\right]\right]_{i}=\delta _{il}\delta _{jm}a_{j}b_{l}c_{m}-\delta _{im}\delta _{jl}a_{j}b_{l}c_{m}=\delta _{il}a_{m}b_{l}c_{m}-\delta _{im}a_{l}b_{l}c_{m}=a_{m}b_{i}c_{m}-a_{l}b_{l}c_{i}=b_{i}({\vec {a}}\cdot {\vec {c}})-c_{i}({\vec {a}}\cdot {\vec {b}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c60555540b1a6169c2d6355eb0e421d7c3fa5de)
ааДаЕбб аИбаПаОаЛбаЗаОаВаАаНаО баВаОаЙббаВаО аДаЕаЛббб абаОаНаЕаКаЕбаА, аПаОаЗаВаОаЛбббаЕаЕ аЗаАаМаЕаНббб аИаНаДаЕаКб, аПаО аКаОбаОбаОаМб аИаДаЕб ббаМаМаИбаОаВаАаНаИаЕ б аДаЕаЛббаОаЙ:  аЂаАаКаИаМ аОаБбаАаЗаОаМ, аЂаАаКаИаМ аОаБбаАаЗаОаМ,
![{\displaystyle \left[{\vec {a}},\left[{\vec {b}},{\vec {c}}\right]\right]_{i}=b_{i}({\vec {a}}\cdot {\vec {c}})-c_{i}({\vec {a}}\cdot {\vec {b}}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee8b5a9b21f31b49743c3e8d3eff66a2ec016f1d)
аИ, аПаЕбаЕб
аОаДб аОб аКаОаМаПаОаНаЕаНбаОаВ аКаО аВбаЕаМб аВаЕаКбаОбб, аПаОаЛббаАаЕаМ аИбаКаОаМаОаЕ баОаОбаНаОбаЕаНаИаЕ.
аЂаОаЖаДаЕббаВаО аЏаКаОаБаИ
ааЛб аДаВаОаЙаНаОаГаО аВаЕаКбаОбаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВбаПаОаЛаНбаЕббб баОаЖаДаЕббаВаО аЏаКаОаБаИ:
![{\displaystyle {\big [}{\vec {a}},{\vec {b}},{\vec {c}}{\big ]}+{\big [}{\vec {b}},{\vec {c}},{\vec {a}}{\big ]}+{\big [}{\vec {c}},{\vec {a}},{\vec {b}}{\big ]}={\vec {0}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65448711aa4cd575d4965e41d0803eccf95eb351)
аКаОбаОбаОаЕ аДаОаКаАаЗбаВаАаЕббб баАбаКбббаИаЕаМ баКаОаБаОаК аПаО баОбаМбаЛаЕ ааАаГбаАаНаЖаА:

аЁаМаЕбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ
аЁаМаЕЬбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕЬаНаИаЕ  аВаЕаКбаОбаОаВ аВаЕаКбаОбаОаВ  т баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаА т баКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаА  аНаА аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аНаА аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ  аИ аИ  : :
 . .
ааНаОаГаДаА аЕаГаО аНаАаЗбаВаАбб ббаОаЙаНбаМ баКаАаЛббаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИаЕаМ аВаЕаКбаОбаОаВ, аПаО аВбаЕаЙ аВаИаДаИаМаОббаИ аИаЗ-аЗаА баОаГаО, ббаО баЕаЗбаЛббаАбаОаМ баВаЛбаЕббб баКаАаЛбб (баОбаНаЕаЕ т аПбаЕаВаДаОбаКаАаЛбб).
ааЕаОаМаЕббаИбаЕбаКаИаЙ баМббаЛ: аМаОаДбаЛб баМаЕбаАаНаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб баИбаЛаЕаНаНаО баАаВаЕаН аОаБббаМб аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаДаА, аОаБбаАаЗаОаВаАаНаНаОаГаО аВаЕаКбаОбаАаМаИ  . .
аЁаВаОаЙббаВаА
 - б. аЕ. аПаЕбаЕббаАаНаОаВаКаА аЛбаБбб
аДаВбб
баОаМаНаОаЖаИбаЕаЛаЕаЙ аМаЕаНбаЕб аЗаНаАаК аПбаОаИаЗаВаЕаДаЕаНаИб. абббаДаА баЛаЕаДбаЕб, ббаО
![{\displaystyle \langle \mathbf {a} ,[\mathbf {b} ,\mathbf {c} ]\rangle =\langle [\mathbf {a} ,\mathbf {b} ],\mathbf {c} \rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cc30b02c812893d882f6853dbae562f4e943be3)

- аЁаМаЕбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ
 аВ аЛаЕаВаОаЙ аДаЕаКаАббаОаВаОаЙ баИббаЕаМаЕ аКаОаОбаДаИаНаАб (аВ аОббаОаНаОбаМаИбаОаВаАаНаНаОаМ аБаАаЗаИбаЕ) баАаВаНаО аОаПбаЕаДаЕаЛаИбаЕаЛб аМаАббаИбб, баОббаАаВаЛаЕаНаНаОаЙ аИаЗ аВаЕаКбаОбаОаВ аВ аЛаЕаВаОаЙ аДаЕаКаАббаОаВаОаЙ баИббаЕаМаЕ аКаОаОбаДаИаНаАб (аВ аОббаОаНаОбаМаИбаОаВаАаНаНаОаМ аБаАаЗаИбаЕ) баАаВаНаО аОаПбаЕаДаЕаЛаИбаЕаЛб аМаАббаИбб, баОббаАаВаЛаЕаНаНаОаЙ аИаЗ аВаЕаКбаОбаОаВ  аИ аИ  , аВаЗббаОаМб баО аЗаНаАаКаОаМ ТЋаМаИаНббТЛ: , аВаЗббаОаМб баО аЗаНаАаКаОаМ ТЋаМаИаНббТЛ:
 - а баАббаНаОббаИ,
- абаЛаИ аКаАаКаИаЕ-баО аДаВаА аВаЕаКбаОбаА аКаОаЛаЛаИаНаЕаАбаНб, баО б аЛбаБбаМ ббаЕббаИаМ аВаЕаКбаОбаОаМ аОаНаИ аОаБбаАаЗббб баМаЕбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, баАаВаНаОаЕ аНбаЛб.
- абаЛаИ ббаИ аВаЕаКбаОбаА аЛаИаНаЕаЙаНаО аЗаАаВаИбаИаМб (б. аЕ. аКаОаМаПаЛаАаНаАбаНб, аЛаЕаЖаАб аВ аОаДаНаОаЙ аПаЛаОбаКаОббаИ), баО аИб
баМаЕбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ баАаВаНаО аНбаЛб.
- ааЕаОаМаЕббаИбаЕбаКаИаЙ баМббаЛ т аЁаМаЕбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ
 аПаО аАаБбаОаЛббаНаОаМб аЗаНаАбаЕаНаИб баАаВаНаО аОаБббаМб аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаДаА (баМ. баИббаНаОаК), аОаБбаАаЗаОаВаАаНаНаОаГаО аВаЕаКбаОбаАаМаИ аПаО аАаБбаОаЛббаНаОаМб аЗаНаАбаЕаНаИб баАаВаНаО аОаБббаМб аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаДаА (баМ. баИббаНаОаК), аОаБбаАаЗаОаВаАаНаНаОаГаО аВаЕаКбаОбаАаМаИ  аИ аИ  ; аЗаНаАаК аЗаАаВаИбаИб аОб баОаГаО, баВаЛбаЕббб аЛаИ ббаА ббаОаЙаКаА аВаЕаКбаОбаОаВ аПбаАаВаОаЙ аИаЛаИ аЛаЕаВаОаЙ. ; аЗаНаАаК аЗаАаВаИбаИб аОб баОаГаО, баВаЛбаЕббб аЛаИ ббаА ббаОаЙаКаА аВаЕаКбаОбаОаВ аПбаАаВаОаЙ аИаЛаИ аЛаЕаВаОаЙ.
- ааВаАаДбаАб баМаЕбаАаНаНаОаГаО аПбаОаИаЗаВаЕаДаЕаНаИб аВаЕаКбаОбаОаВ баАаВаЕаН аОаПбаЕаДаЕаЛаИбаЕаЛб абаАаМаА, аОаПбаЕаДаЕаЛбаЕаМаОаМб аИаМаИ[40].
 аЂбаИ аВаЕаКбаОбаА, аОаПбаЕаДаЕаЛбббаИаЕ аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаД. аЂбаИ аВаЕаКбаОбаА, аОаПбаЕаДаЕаЛбббаИаЕ аПаАбаАаЛаЛаЕаЛаЕаПаИаПаЕаД.

- (аВ аПаОбаЛаЕаДаНаЕаЙ баОбаМбаЛаЕ аВ аОббаОаНаОбаМаИбаОаВаАаНаНаОаМ аБаАаЗаИбаЕ аВбаЕ аИаНаДаЕаКбб аМаОаЖаНаО аПаИбаАбб аНаИаЖаНаИаМаИ; аВ ббаОаМ баЛббаАаЕ ббаА баОбаМбаЛаА баОаВаЕббаЕаНаНаО аПббаМаО аПаОаВбаОббаЕб баОбаМбаЛб б аОаПбаЕаДаЕаЛаИбаЕаЛаЕаМ, аПбаАаВаДаА, аПбаИ ббаОаМ аАаВбаОаМаАбаИбаЕбаКаИ аПаОаЛббаАаЕббб аМаНаОаЖаИбаЕаЛб (-1) аДаЛб аЛаЕаВбб
аБаАаЗаИбаОаВ).
абаИаМаЕаНаЕаНаИаЕ аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб аК ббаЕбаИбаЕбаКаОаЙ аГаЕаОаМаЕббаИаИ аИ ббаИаГаОаНаОаМаЕббаИаИ
аЂаЕаОбаЕаМб ббаЕбаИбаЕбаКаОаЙ аГаЕаОаМаЕббаИаИ аИ ббаИаГаОаНаОаМаЕббаИаИ аИаЗббаНаО аДаОаКаАаЗбаВаАбббб аВ баАаМаКаАб
аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб[41].
аббаАаЖаЕаНаИаЕ ббаОбаОаН аИ баГаЛаОаВ ббаЕбаИбаЕбаКаОаГаО ббаЕбаГаОаЛбаНаИаКаА
абаИаМаЕбаАаНаИб
- т 1 2 ааАаПбаЕаВ а. аЄ. ааЛаЕаМаЕаНбб аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1975, ааЛаАаВаА III. абаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ. ТЇ 1. аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аДаВбб
аВаЕаКбаОбаОаВ, б. 43.
- т 1 2 3 ааОбаИаН а. аЄ. ааЕаКбаОбаНаОаЕ аИббаИбаЛаЕаНаИаЕ аИ аНаАбаАаЛаА баЕаНаЗаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1965, ТЇ 5. аЁаКаАаЛббаНаОаЕтІ аПбаОаИаЗаВаЕаДаЕаНаИаЕтІ, б. 35.
- т ааАаПбаЕаВ а. аЄ. ааЛаЕаМаЕаНбб аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1975, ааЛаАаВаА III. абаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ. ТЇ 1. аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аДаВбб
аВаЕаКбаОбаОаВ, б. 43т44.
- т ааИаЛаН-аЂаОаМбаОаН а. а. аЂаЕаОбаЕбаИбаЕбаКаАб аГаИаДбаОаДаИаНаАаМаИаКаА, 1965, 2.16. ааНаДаЕбаИаНаИбаНаОаЕ, аИаЛаИ аДаИаАаДаНаОаЕ, аПбаОаИаЗаВаЕаДаЕаНаИаЕ, б. 41.
- т ааАаПбаЕаВ а. аЄ. ааЛаЕаМаЕаНбб аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1975, ааЛаАаВаА IV. абаОаИаЗаВаЕаДаЕаНаИб бббб
аВаЕаКбаОбаОаВ. ТЇ 1. абаОббаЕаЙбаЕаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ бббб
аВаЕаКбаОбаОаВ, б. 58т59.
- т 1 2 ааОбаИаН а. аЄ. ааЕаКбаОбаНаОаЕ аИббаИбаЛаЕаНаИаЕ аИ аНаАбаАаЛаА баЕаНаЗаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1965, ТЇ 7. абаОаИаЗаВаЕаДаЕаНаИб бббб
аВаЕаКбаОбаОаВ.тІ, б. 59.
- т 1 2 3 4 5 ааАаПбаЕаВ а. аЄ. ааЛаЕаМаЕаНбб аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1975, ааЛаАаВаА IV. абаОаИаЗаВаЕаДаЕаНаИб бббб
аВаЕаКбаОбаОаВ. ТЇ 1. абаОббаЕаЙбаЕаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ бббб
аВаЕаКбаОбаОаВ, б. 59.
- т ааОбаИаН а. аЄ. ааЕаКбаОбаНаОаЕ аИббаИбаЛаЕаНаИаЕ аИ аНаАбаАаЛаА баЕаНаЗаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1965, ТЇ 7. абаОаИаЗаВаЕаДаЕаНаИб бббб
аВаЕаКбаОбаОаВ.тІ, б. 64.
- т ааОбаН-аЂаАаНаНбаДаЖаИ а., ааИб а., ааАаЛаОб аЄ. ааВаАаНбаОаВаАб аМаЕб
аАаНаИаКаА. аЂаОаМ I, 2000, ааЛаАаВаА а. ааАбаЕаМаАбаИбаЕбаКаИаЙ аАаПаПаАбаАб аКаВаАаНбаОаВаОаЙ аМаЕб
аАаНаИаКаИ. B. абаОбббаАаНббаВаО баОббаОбаНаИаЙ. ааБаОаЗаНаАбаЕаНаИб ааИбаАаКаА. 2. ааЕаКбаОбб ТЋаКаЕбТЛ аИ аВаЕаКбаОбб ТЋаБбаАТЛ. аЌ. ааЛаЕаМаЕаНбб аВ аДбаАаЛбаНаОаМ аПбаОбббаАаНббаВаЕ
 : аБбаА-аВаЕаКббб. : аБбаА-аВаЕаКббб.  . ааБаОаЗаНаАбаЕаНаИаЕ ТЋаБбаАТЛ аДаЛб аВаЕаКбаОбаОаВ аПбаОбббаАаНббаВаА . ааБаОаЗаНаАбаЕаНаИаЕ ТЋаБбаАТЛ аДаЛб аВаЕаКбаОбаОаВ аПбаОбббаАаНббаВаА  , б. 133. , б. 133.
- т 1 2 абббаЕаВ аЎ. а. ааЕаКбаОбаНаАб аАаЛаГаЕаБбаА, 1977, б. 634.
- т 1 2 3 4 абббаЕаВ аЎ. а. ааЕаКбаОбаНаАб аАаЛаГаЕаБбаА, 1988, б. 108.
- т 1 2 3 4 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 4. ааОбаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 328.
- т ааЕаЛббаАаНаД а. а. ааЕаКбаИаИ аПаО аЛаИаНаЕаЙаНаОаЙ аАаЛаГаЕаБбаЕ, 1971, ТЇ 2. ааВаКаЛаИаДаОаВаО аПбаОбббаАаНббаВаО. 1. ааПбаЕаДаЕаЛаЕаНаИаЕ аЕаВаКаЛаИаДаОаВаА аПбаОбббаАаНббаВаА, б. 30т31.
- т ааАаПбаЕаВ а. аЄ. ааЛаЕаМаЕаНбб аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1975, ааЛаАаВаА III. абаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ. ТЇ 1. аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аДаВбб
аВаЕаКбаОбаОаВ, б. 44.
- т 1 2 3 ааВаАаНаОаВ а. а. абаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, 1984.
- т 1 2 абббаЕаВ аЎ. а. ааЕаКбаОбаНаАб аАаЛаГаЕаБбаА, 1977, б. 635.
- т 1 2 3 4 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 4. ааОбаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 341.
- т 1 2 абаАбаОаЛаОаВ а. а. ааАаДаАбаИ аПаО аПаЛаАаНаИаМаЕббаИаИ, 2006, ааЛаАаВаА 13. ааЕаКбаОбб. ТЇ 7. абаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, б. 313.
- т 1 2 3 4 5 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 3. аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 336.
- т 1 2 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 3. аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 336т337.
- т 1 2 3 4 5 6 7 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 3. аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 337.
- т 1 2 3 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 5. аЂбаОаЙаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аИ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аПбаОбббаАаНббаВаА, б. 364т365.
- т 1 2 3 4 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 3. аЁаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 338.
- т абаДббаВбаЕаВ а. а. аббб аМаАбаЕаМаАбаИбаЕбаКаОаГаО аАаНаАаЛаИаЗаА. аЂ. 2, 1981, 57.7. ааИаНаЕаЙаНбаЕ аПбаОбббаАаНббаВаА баО баКаАаЛббаНбаМ аПбаОаИаЗаВаЕаДаЕаНаИаЕаМ, б. 447.
- т абаДббаВбаЕаВ а. а. аббб аМаАбаЕаМаАбаИбаЕбаКаОаГаО аАаНаАаЛаИаЗаА. аЂ. 2, 1970, 57.4. ааИаЛбаБаЕббаОаВб аИ аПбаЕаДаГаИаЛбаБаЕббаОаВб аПбаОбббаАаНббаВаА, б. 316.
- т ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 4. ааОбаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 338т341.
- т Ivanov A. B. Pseudo-scalar product, 2020.
- т 1 2 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 4. ааОбаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 342.
- т ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 4. ааОбаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 342т343.
- т 1 2 3 4 5 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 4. ааОбаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ, б. 343.
- т 1 2 3 4 5 6 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 4. ааОбаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аПаЛаОбаКаОббаИ, б. 349.
- т 1 2 3 4 5 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 4. ааОбаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аПаЛаОбаКаОббаИ, б. 350.
- т 1 2 3 4 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 5. аЂбаОаЙаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аИ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аПбаОбббаАаНббаВаА, б. 364.
- т 1 2 3 4 5 6 7 8 9 10 ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 5. аЂбаОаЙаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аИ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аПбаОбббаАаНббаВаА, б. 365.
- т ааИаЛаН-аЂаОаМбаОаН а. а. аЂаЕаОбаЕбаИбаЕбаКаАб аГаИаДбаОаДаИаНаАаМаИаКаА, 1965, 2.14. аЂбаОаЙаНаОаЕ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, б. 40.
- т Weisstein Eric W. Vector Triple Product, 2024.
- т ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 5. аЂбаОаЙаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аИ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВ аПбаОбббаАаНббаВаА, б. 360.
- т абаГаОаДбаКаИаЙ а. аЏ. аЁаПбаАаВаОбаНаИаК аПаО аВбббаЕаЙ аМаАбаЕаМаАбаИаКаЕ, 1977, ТЇ 122. ааВаОаЙаНаОаЕ аВаЕаКбаОбаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ, б. 182.
- т 1 2 ааАаПбаЕаВ а. аЄ. ааЛаЕаМаЕаНбб аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб, 1975, ааЛаАаВаА III. абаОаИаЗаВаЕаДаЕаНаИб аДаВбб
аВаЕаКбаОбаОаВ. ТЇ 1. абаОббаЕаЙбаЕаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ бббб
аВаЕаКбаОбаОаВ, б. 59.
- т аббббаНаИаКаОаВ а. а., а аЕаЗаНаИбаЕаНаКаО аЁ. а. ааЕаКбаОбаНаАб аАаЛаГаЕаБбаА аВ аПбаИаМаЕбаАб
аИ аЗаАаДаАбаАб
, 1985, ааЛаАаВаА 4. ааЕаКбаОбаНаОаЕ аИ баМаЕбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИб. ТЇ 4. аЁаМаЕбаАаНаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ аВаЕаКбаОбаОаВтІ абаИаМаЕб 19*, б. 215.
- т ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ, 1963, ТЇ 6. абаИаМаЕаНаЕаНаИаЕ аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб аК ббаЕбаИбаЕбаКаОаЙ аГаЕаОаМаЕббаИаИ аИ ббаИаГаОаНаОаМаЕббаИаИ, б. 366.
аббаОбаНаИаКаИ
- ааОаЛббаНбаКаИаЙ а. а., аЏаГаЛаОаМ а. а. ааЕаКбаОбб аИ аИб
аПбаИаМаЕаНаЕаНаИб аВ аГаЕаОаМаЕббаИаИ // ааНбаИаКаЛаОаПаЕаДаИб баЛаЕаМаЕаНбаАбаНаОаЙ аМаАбаЕаМаАбаИаКаИ, аКаНаИаГаА баЕбаВбббаАб т аГаЕаОаМаЕббаИб / ааЛ. баЕаД. а. аЁ. ааЛаЕаКбаАаНаДбаОаВ, а. а. ааАбаКббаЕаВаИб, а. аЏ. аЅаИаНбаИаН. а аЕаД. аКаНаИаГаИ 4: а. а. ааОаЛббаНбаКаИаЙ, а. а. аЏаГаЛаОаМ. а.: аЄаИаЗаМаАбаГаИаЗ, 1963. 568 б., аИаЛ. аЁ. 291т381.
- абаГаОаДбаКаИаЙ а. аЏ. аЁаПбаАаВаОбаНаИаК аПаО аВбббаЕаЙ аМаАбаЕаМаАбаИаКаЕ. ааЗаД-аЕ 12-аЕ, ббаЕбаЕаОбаИаП. а.: ааАбаКаА, 1977. 871 б., аИаЛ.
- ааЕаЛббаАаНаД а. а. ааЕаКбаИаИ аПаО аЛаИаНаЕаЙаНаОаЙ аАаЛаГаЕаБбаЕ. ааЗаД. 4-аЕ, аДаОаП. а.: ааАбаКаА, 1971. 271 б., аИаЛ.
- аббббаНаИаКаОаВ а. а., а аЕаЗаНаИбаЕаНаКаО аЁ. а. ааЕаКбаОбаНаАб аАаЛаГаЕаБбаА аВ аПбаИаМаЕбаАб
аИ аЗаАаДаАбаАб
: аЃбаЕаБ. аПаОбаОаБаИаЕ аДаЛб бббаДаЕаНбаОаВ аИаНаЖ.-баЕб
. баПаЕб. аВбаЗаОаВ. а.: абббаАб баКаОаЛаА, 1985. 232 б., аИаЛ.
- ааВаАаНаОаВ а. а. абаЕаВаДаОбаКаАаЛббаНаОаЕ аПбаОаИаЗаВаЕаДаЕаНаИаЕ // ааАбаЕаМаАбаИбаЕбаКаАб баНбаИаКаЛаОаПаЕаДаИб: ааЛ. баЕаД. а. а. ааИаНаОаГбаАаДаОаВ, б. 4 ааКтаЁаЛаО. а.: ТЋаЁаОаВаЕббаКаАб ааНбаИаКаЛаОаПаЕаДаИбТЛ, 1984. 1216 ббаБ., аИаЛ. аЁбаБ. 743.
- ааОбаИаН а. аЄ. ааЕаКбаОбаНаОаЕ аИббаИбаЛаЕаНаИаЕ аИ аНаАбаАаЛаА баЕаНаЗаОбаНаОаГаО аИббаИбаЛаЕаНаИб. ааЗаД-аЕ 9-аЕ. а.: ааАбаКаА, 1965. 427 б., аИаЛ.
- ааОбаН-аЂаАаНаНбаДаЖаИ а., ааИб а.[бб.], ааАаЛаОб аЄ.[аАаНаГаЛ.] ааВаАаНбаОаВаАб аМаЕб
аАаНаИаКаА. а 2 б. аЂаОаМ I / ааЕбаЕаВаОаД б ббаАаНббаЗбаКаОаГаО а. а. ааОаВаИаКаОаВаА. ааКаАбаЕбаИаНаБббаГ: ааЗаДаАбаЕаЛбббаВаО аЃбаАаЛббаКаОаГаО баНаИаВаЕббаИбаЕбаА, 2000. 942 б., аИаЛ. ISBN 5-7525-1085-6 ISBN 5-7525-1131-3 (T. I) [Cohen-Tannoudji, Claude; Diu, Bernard; LaloУЋ, Franck Quantum mechanics, Volume 1: Basic Concepts, Tools, and Applications. Paris: Hermann, 1973.]
- абаДббаВбаЕаВ а. а. аббб аМаАбаЕаМаАбаИбаЕбаКаОаГаО аАаНаАаЛаИаЗаА (аВ аДаВбб
баОаМаАб
): аЃбаЕаБаНаИаК аДаЛб бббаДаЕаНбаОаВ баНаИаВаЕббаИбаЕбаОаВ аИ аВббаЗаОаВ. а.: абббаАб баКаОаЛаА, 1981, б. II: т 584 б, аИаЛ.
- абаДббаВбаЕаВ а. а. аббб аМаАбаЕаМаАбаИбаЕбаКаОаГаО аАаНаАаЛаИаЗаА (аВ аДаВбб
баОаМаАб
): аЃбаЕаБаНаИаК аДаЛб бббаДаЕаНбаОаВ баНаИаВаЕббаИбаЕбаОаВ аИ аВббаЗаОаВ. а.: абббаАб баКаОаЛаА, 1970, б. II.
- ааАаПбаЕаВ а. аЄ. ааЛаЕаМаЕаНбб аВаЕаКбаОбаНаОаГаО аИббаИбаЛаЕаНаИб. а.: ааАбаКаА, 1975. 336 б., аИаЛ.
- ааИаЛаН-аЂаОаМбаОаН а. а.[аАаНаГаЛ.] аЂаЕаОбаЕбаИбаЕбаКаАб аГаИаДбаОаДаИаНаАаМаИаКаА / ааЕбаЕаВаОаД б аАаНаГаЛаИаЙбаКаОаГаО а. а. ааЕббаОаВаА, аЏ. а. аЁаЕаКаЕбаЖ-ааЕаНбаКаОаВаИбаА аИ а. а. аЇббаКаИаНаА аПаОаД баЕаДаАаКбаИаЕаЙ а. а. ааОаИбаЕаЕаВаА. а.: ТЋааИбТЛ, 1964. 660 б., аИаЛ. [Milne-Thomson, L. M. Theoretical hydrodynamics. Fourth edition. London: Macmillan and Co. LTD ТЗ New York: St. Martin's Press, 1960.]
- абаАбаОаЛаОаВ а. а. ааАаДаАбаИ аПаО аПаЛаАаНаИаМаЕббаИаИ: аЃбаЕаБаНаОаЕ аПаОбаОаБаИаЕ. 5-аЕ аИаЗаД., аИбаПб. аИ аДаОаП. а.: ааІааа: ааа ТЋааОбаКаОаВбаКаИаЕ ббаЕаБаНаИаКаИТЛ, 2006. 640 б.: аИаЛ. ISBN 5-94057-214-6.
- абббаЕаВ аЎ. а. ааЕаКбаОбаНаАб аАаЛаГаЕаБбаА // ааАбаЕаМаАбаИбаЕбаКаАб баНбаИаКаЛаОаПаЕаДаИб: ааЛ. баЕаД. а. а. ааИаНаОаГбаАаДаОаВ, б. 1 ата. а.: ТЋаЁаОаВаЕббаКаАб ааНбаИаКаЛаОаПаЕаДаИбТЛ, 1977. 1152 ббаБ., аИаЛ. аЁбаБ. 632т636.
- абббаЕаВ аЎ. а. ааЕаКбаОбаНаАб аАаЛаГаЕаБбаА // ааАбаЕаМаАбаИбаЕбаКаИаЙ баНбаИаКаЛаОаПаЕаДаИбаЕбаКаИаЙ баЛаОаВаАбб / ааЛ. баЕаД. аЎ. а. абаОб
аОбаОаВ; а аЕаД. ааОаЛ.: аЁ. а. ааДбаН, а. аЁ. ааАб
аВаАаЛаОаВ, а. а. ааИбббаКаОаВ, а. а. аббаОаВ, а. а. абаДббаВбаЕаВ, а. а. ааНаИбаИаК, а. а. аЎбаКаЕаВаИб. а.: ТЋаЁаОаВаЕббаКаАб баНбаИаКаЛаОаПаЕаДаИбТЛ, 1988. 847 б., аИаЛ. аЁ. 107т109.
- Ivanov A. B. Pseudo-scalar product. 2020 // Encyclopedia of Mathematics. 2020. абб
аИаВаНаАб аКаОаПаИб аОб 28 аАаПбаЕаЛб 2023 аНаА Wayback Machine
- Weisstein Eric W. Vector Triple Product // Wolfram MathWorld абб
аИаВаНаАб аКаОаПаИб аОб 2 аИбаНб 2024 аНаА Wayback Machine
 ааЕаКбаОбб аИ аМаАббаИбб |
|---|
| ааЕаКбаОбб | | абаНаОаВаНбаЕ аПаОаНббаИб | |
|---|
| ааИаДб аВаЕаКбаОбаОаВ | |
|---|
| ааПаЕбаАбаИаИ аНаАаД аВаЕаКбаОбаАаМаИ | |
|---|
| аЂаИаПб аПбаОбббаАаНббаВ | |
|---|
|
|---|
| ааАббаИбб | |
|---|
| аббаГаОаЕ | |
|---|
|
|