ะงะตััััั ัะณะพะปัะฝะธะบ ะกะฐะบะบะตัะธ
|
Read other articles:

Cheil WorldwideNama asli์ ์ผ๊ธฐํ (็ฌฌไธไผๅ)JenisPublikKode emitenKRX: 030000IndustriPeriklananDidirikan1973; 51 tahun lalu (1973)KantorpusatSeoul, Korea SelatanWilayah operasiSeluruh duniaTokohkunciJeongkeun Yoo[1] (Presiden & CEO)Jasaperiklanan hubungan masyarakat pemasaran belanja pemasaran olahraga pemasaran digitalPendapatanUSD $984,9 juta (2018)[2]PemilikSamsungIndukSamsung Electronics (28,43%)AnakusahaSamsung SportsSitus webCheil.com/ Cheil Worldwide Inc...

Mildef Tarantula High Mobility Armoured Vehicle Purwarupa Tarantula HMAV 4x4 Jenis Pengangkut personel lapis baja / MRAP Negara asal Malaysia Sejarah pemakaian Masa penggunaan 2021 โ Sekarang Digunakan oleh Malaysia Pada perang Tidak ada Sejarah produksi Tahun 2013 Produsen Mildef International Technologies Diproduksi 2021 โ sekarang Jumlah produksi 4 (2 purwarupa)[1] Spesifikasi Berat 14 ton (berat kotor), 11 ton (berat kosong) Panjang 5.6 me...

ุณูุงุฑุฉ ุฃููุฑุงููุง ูู ุณููุณุฑุง ุฃููุฑุงููุง ุณููุณุฑุง ุงูุฅุญุฏุงุซูุงุช 46ยฐ56โฒ38โณN 7ยฐ26โฒ50โณE / 46.943925ยฐN 7.4470888888889ยฐE / 46.943925; 7.4470888888889 ุงูุจูุฏ ุณููุณุฑุง ุงูู ูุงู ุจุฑู ุงูุงุฎุชุตุงุต ุณููุณุฑุง ุงูู ููุน ุงูุงููุชุฑููู ุงูู ููุน ุงูุฑุณู ู ุชุนุฏูู ู ุตุฏุฑู - ุชุนุฏูู ุณูุงุฑุฉ ุฃููุฑุงููุง ูู ุณููุณุฑุง ูู ุฃุฑูุน ุชู ุซูู ุฏุจููู ุงุณู[1...

Ne doit pas รชtre confondu avec Alexandre Jacob (peintre). Pour les articles homonymes, voir Jacob (homonymie). Marius JacobPhotographie d'identitรฉ judiciaire de Marius Jacob, 1903.BiographieNaissance 29 septembre 1879MarseilleDรฉcรจs 28 aoรปt 1954 (ร 74 ans)ReuillyNationalitรฉ franรงaiseActivitรฉs Cambrioleur, marin, anarchiste, typographeAutres informationsCondamnation Bagnemodifier - modifier le code - modifier Wikidata Alexandre Marius Jacob, dit Marius Jacob, nรฉ le 29 septembre ...

Ukrainian politician In this name that follows Eastern Slavic naming customs, the patronymic is Viacheslavovych and the family name is Chornovil. Taras Chornovilะขะฐัะฐั ะงะพัะฝะพะฒัะปChornovil in 2011People's Deputy of UkraineIn office5 July 2000 โ 15 December 2012[1]Preceded by Roman Schmidt (2000) Mykhailo Kosiv (2002)[2] Succeeded byConstituency abolishedConstituency Lviv Oblast, No. 115 (2000โ2002) Lviv Oblast, No. 116 (2002โ2006) Party of Regions, ...
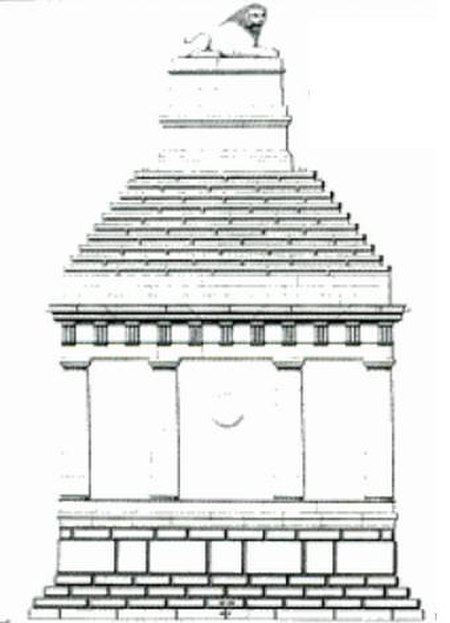
Ancient Greek statue Lion of KnidosLion of KnidosMaterialMarbleSize2.89 m long by 1.82 m highCreatedc. 350โ200 BCPresent locationBritish Museum, LondonRegistration1859,1226.24 The Lion of Knidos is the name for a colossal ancient Greek statue erected near the ancient port of Knidos, south-west Asia Minor (now near Datรงa in Turkey). Although there is some debate about the age of the sculpture, in general, scholarly opinion dates it to the 2nd century BC. Since 2000, it has been promin...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: The Forest Rangers band โ news ยท newspapers ยท books ยท scholar ยท JSTOR (December 2015) (Learn how and when to remove this message) A major contributo...

ะฅัะธััะธะฐะฝััะฒะพะะธะฑะปะธั ะะตัั ะธะน ะะฐะฒะตั ะะพะฒัะน ะะฐะฒะตั ะะฒะฐะฝะณะตะปะธะต ะะตัััั ะทะฐะฟะพะฒะตะดะตะน ะะฐะณะพัะฝะฐั ะฟัะพะฟะพะฒะตะดั ะะฟะพะบัะธัั ะะพะณ, ะขัะพะธัะฐ ะะพะณ ะัะตั ะะธััั ะฅัะธััะพั ะกะฒััะพะน ะัั ะััะพัะธั ั ัะธััะธะฐะฝััะฒะฐ ะะฟะพััะพะปั ะฅัะพะฝะพะปะพะณะธั ั ัะธััะธะฐะฝััะฒะฐ ะ ะฐะฝะฝะตะต ั ัะธััะธะฐะฝััะฒะพ ะะฝะพััะธัะตัะบะพะต ั ัะธััะธะฐะฝััะฒะพ ะัะตะปะตะฝัะบะธะต ัะพะฑะพัั ะ...

Largest desert in North America Chihuahuan DesertChihuahuan desert landscape in Big Bend National ParkLocation map of Chihuahuan DesertEcologyRealmNearcticBiomeDeserts and xeric shrublandsBorders List Arizona Mountains forestsColorado Plateau shrublandsEdwards Plateau savannaMeseta Central matorralSierra Madre Occidental pineโoak forestsSierra Madre Oriental pineโoak forestsSonoran DesertTamaulipan matorralTamaulipan mezquitalWestern short grasslands GeographyArea501,896 km2 (193,783...

Sceaux ่กๆฟๅฝ ใใฉใณในๅฐๅๅ (Rรฉgion) ใคใซ๏ผใ๏ผใใฉใณในๅฐๅๅ็ (dรฉpartement) ใชใผ๏ผใ๏ผใปใผใ็้ก (arrondissement) ใขใณใใใผ้กๅฐ้ก (canton) ๅฐ้กๅบๆๅจๅฐINSEEใณใผใ 92071้ตไพฟ็ชๅท 92330ๅธ้ท๏ผไปปๆ๏ผ ใใฃใชใใใปใญใผใฉใณ๏ผ2008ๅนด-2014ๅนด๏ผ่ชๆฒปไฝ้้ฃๅ (fr) ใกใใญใใผใซใปใใฅใปใฐใฉใณใปใใชไบบๅฃๅๆ ไบบๅฃ 19,679ไบบ๏ผ2007ๅนด๏ผไบบๅฃๅฏๅบฆ 5466ไบบ/km2ไฝๆฐใฎๅผ็งฐ Scรฉensๅฐ็ๅบงๆจ ๅ็ทฏ48ๅบฆ4...

French physicist Catherine BrรฉchignacCatherine Brรฉchignac in 2006Born (1946-06-12) 12 June 1946 (age 77)Paris, FranceNationalityFrenchAlma materรcole Normale Supรฉrieure de LyonFacultรฉ des sciences d'OrsayAwardsGrand Officier of the Lรฉgion d'honneurMany others, see articleScientific careerFieldsPhysicsInstitutionsCNRS Catherine Brรฉchignac (French pronunciation: [katสin bสeสiษฒak] โ; born 12 June 1946) is a French physicist. She is a commander of the Lรฉgion d'honn...

AwardJacques Deray PrizeAwarded forBest French Policier Film of the YearCountryFrancePresented byInstitut LumiรจreFirst awarded2005Currently held byAnatomy of a Fall (2024)Websitewww.institut-lumiere.org The Jacques Deray Prize (French: Prix Jacques-Deray) is a French film award presented annually since 2005. It celebrates the memory of the director Jacques Deray, who was known for directing many crime and thriller films. It was created by the Institut Lumiรจre in collaboration with the Asso...

Christian theological concept For a broader description about communication from deity, see revelation. In theology, general revelation, or natural revelation,[1] refers to God's revelation made to all men everywhere,[1] discovered through natural means, such as observation of nature (the physical universe), philosophy, and reasoning. Christian theologians use the term to describe knowledge of God purported to be plainly available to all mankind. General revelation is usually ...

Experimental Japanese train class The Gauge Change Train (GCT) or Free Gauge Train (ใใชใผใฒใผใธใใฌใคใณ, FGT) is the name given to a Japanese project started in 1994 to develop a high-speed train with variable gauge axles to allow inter-running between the 1,435 mm (4 ft 8+1⁄2 in) standard gauge Shinkansen network, and the 1,067 mm (3 ft 6 in) narrow gauge regional rail network.[1] Two three-car and one four-car GCT electric mul...

U.S. state flag Bear flag redirects here. For other uses, see Bear flag (disambiguation). Bear FlagFlag of CaliforniaThe Bear FlagUseCivil and state flag, state ensign Proportion2:3AdoptedFebruary 3, 1911; 113 years ago (1911-02-03) (standardized 1953)DesignA single red star in the canton, a red stripe along the bottom, and a California grizzly bear atop a mound of green grass defacing a white field.Designed byDonald Graeme Kelley, based on flag flown during the Bear Fl...

Les districts de gouvernement local depuis 2015. 1 : Belfast 2 : Ards and North Down 3 : Antrim and Newtownabbey 4 : Lisburn and Castlereagh 5 : Newry, Mourne and Down 6 : Armagh City, Banbridge and Craigavon 7 : Mid and East Antrim 8 : Causeway Coast and Glens 9 : Mid Ulster 10 : Derry City and Strabane 11 : Fermanagh and Omagh Depuis le 1er avril 2015, lโIrlande du Nord se subdivise en onze districts de gouvernement local dโinรฉgale...

Season of television series Season of television series Spy ร FamilySeason 1Japanese cover art for the first home media volume of the season, featuring Loid Forger / TwilightNo. of episodes25ReleaseOriginal networkTV TokyoOriginal releaseApril 9 (2022-04-09) โDecember 24, 2022 (2022-12-24)Season chronologyNext โSeason 2List of episodes The first season of the Spy ร Family anime television series was produced by Wit Studio and CloverWorks. The series is directed by Ka...

BeatoKaspar StanggassingerC.Ss.R.ImamLahir(1871-01-12)12 Januari 1871Berchtesgaden, Oberbayern, Kekaisaran JermanMeninggal26 September 1899(1899-09-26) (umur 28)Gars am Inn, Oberbayern, Kekaisaran JermanDihormati diGereja Katolik RomaBeatifikasi24 April 1988, Lapangan Santo Petrus, Kota Vatikan oleh Paus Yohanes Paulus IIPesta26 SeptemberAtributBusana imam Kaspar Stanggassinger (12 Januari 1871 – 26 September 1899) adalah seorang imam Katolik Roma asal Jerman dan anggota ...

Croteam Ltd.็จฎ้ก ้ไธๅ ดไผๆฅญๆฌ็คพๆๅจๅฐ ใฏใญใขใใขใถใฐใฌใ่จญ็ซ 1993ๅนด; 24 ๅนดๅ (1993)ๆฅญ็จฎ ใใใชใฒใผใ ไบๆฅญๅ ๅฎน Serious Sam The Talos Principleไปฃ่กจ่ ใญใผใใณใปใชใใชใใฏ (CEO) ใขใฌใณใปใฉใใดใกใใฏ (CTO) ใใดใฉใผใซใปใใณในใญ (CCO) ใใใขใณใปใ ใฉใดใใใฏ (CMO)ๆๆ่ Devolver Digitalใใณใใฌใผใใ่กจ็คบCroteam Ltd. ใฏใฏใญใขใใขใฎใถใฐใฌใใซๆ ็นใ็ฝฎใใณใณใใฅใผ๏ฟฝ...

Historic region of Germany Rhenish redirects here. For other uses, see Rhenish (disambiguation) and Rhineland (disambiguation). This article is about the Rhineland as a region. For the historical period from 1822 until 1946, see Rhine Province. You can help expand this article with text translated from the corresponding article in German. (September 2018) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point f...














