Трансцендентное число
|
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Esther A. Howland – berita · surat kabar · buku · cendekiawan · JSTOR Esther Allen HowlandLahir(1828-08-17)17 Agustus 1828Worcester, MassachusettsMeninggal15 Maret 1904(1904-03-15) (umur 75)Quincy, ...

فروة بن عمرو الأنصاري زخرفة لاسم الصحابي فروة بن عمرو الأنصاري ومع الدعاء رضي الله عنه معلومات شخصية اسم الولادة فروة بن عمرو الأنصاري مكان الميلاد المدينة المنورة الزوجة حبيبة بنت مُليل بن وَبَرَةآمنة بنت خليفة بن عديّ الأب عمرو بن ودقة الأم رحيمة بنت نابىء بن زيد[1] �...

المراجعة العاشرة للتصنيف الدولي للأمراضمعلومات عامةالاسم المختصر МКБ-10 (بالروسية) ICD-10 (بالإنجليزية) جزءٌ مِن سلسلة التصنيف الدولي للأمراض له طبعات أو ترجمات في ICD-10 Online version (2010) (en) ICD-10 German Modification (en) ICD-10 Chapter V: Russian Adaption (en) طبعة أو ترجمة لـ التصنيف الدولي للأمراض المُؤَلِّف من...

Keuangan bagian dari Ekonomi Pasar uangPasar Bond · Pasar bursa efek (Ekuitas) · Devisa · Derivatif · Komoditi · Uang · Spot (tunai) · Pasar OTC · Real estat · Ekuitas swasta Pelaku pasarInvestor · Spekulan · Lembaga Investor Keuangan korporasiStruktur keuangan · Penganggaran pemodalan · Manajemen risiko keuangan · Merger dan A...

Pour les articles homonymes, voir Drumont. Édouard DrumontÉdouard Drumont vers 1880.FonctionDéputé françaisDépartement d'Alger1898-1902Paul SamaryMaurice ColinBiographieNaissance 3 mai 1844ParisDécès 5 février 1917 (à 72 ans)17e arrondissement de ParisSépulture Cimetière du Père-Lachaise, Grave of Drumont (d)Nom de naissance Édouard Adolphe DrumontNationalité françaiseFormation Lycée CondorcetActivité Écrivain, journaliste, homme politiqueConjoints Louise Gayte (...

German football manager (born 1965) Hansi Flick Flick in 2022Personal informationFull name Hans-Dieter Flick[1]Date of birth (1965-02-24) 24 February 1965 (age 59)Place of birth Heidelberg, West GermanyHeight 1.77 m (5 ft 10 in)Position(s) MidfielderYouth career1971–1976 BSC Mückenloch1976–1981 SpVgg Neckargemünd1981–1983 SV SandhausenSenior career*Years Team Apps (Gls)1982–1985 SV Sandhausen 69 (8)1985–1990 Bayern Munich 104 (5)1990–1993 1. FC Köln ...

Building in New York City, United States of AmericaThe Church of St. DominicSt. Dominic's Church in Van NestGeneral informationArchitectural styleRomanesque RevivalTown or cityVan Nest, Bronx, New York CityCountryUnited States of AmericaConstruction startedMay 31, 1925ClientRoman Catholic Archdiocese of New YorkTechnical detailsStructural systemBrick masonryDesign and constructionArchitect(s)Anthony J. DePace of the firm DePace & Juster The Church of St. Dominic is a Roman Catholic parish...
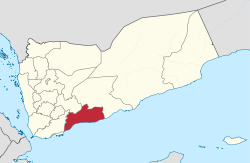
Governorate of Yemen Abyan redirects here. For the village in Iran, see Abyan, Iran. Governorate in Aden Region, YemenAbyan أَبْيَنْGovernorateCountry YemenRegionAden RegionSeatZinjibarArea • Total21,939 km2 (8,471 sq mi)Population (2012)[1] • Total513,701 • Density23/km2 (61/sq mi)Time zoneUTC+3 (Arabia Standard Time) Abyan (Arabic: أَبْيَنْ ʾAbyan) is a governorate of Yemen. The Abyan region was histo...

Due DatePoster filmSutradaraTodd PhillipsProduserTodd PhillipsDaniel GoldbergSusan DowneySkenarioAlan R. CohenAlan FreedlandAdam SztykielTodd PhillipsCeritaAlan R. CohenAlan FreedlandPemeranRobert Downey Jr.Zach GalifianakisMichelle MonaghanJuliette LewisJamie FoxxPenata musikChristophe BeckSinematograferLawrence SherPenyuntingDebra Neil-FisherPerusahaanproduksiLegendary PicturesGreen Hat FilmsDistributorWarner Bros. PicturesTanggal rilis 31 Oktober 2010 (2010-10-31) (Night Vis...

Cet article est une ébauche concernant le Danemark et le Concours Eurovision de la chanson. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Danemarkau Concours Eurovision 1958 Raquel Rastenni représentant le Danemark avec la chanson Jeg rev et blad ud af min dagbog au Concours Eurovision de la chanson 1958 à Hilversum. Données clés Pays Danemark Chanson Jeg rev et blad ud af min dagbog Interprète Raq...

† Египтопитек Реконструкция внешнего вида египтопитека Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:Четвероно...

For related races, see 1920 United States gubernatorial elections. 1920 Delaware gubernatorial election ← 1916 November 2, 1920 1924 → Nominee William D. Denney Andrew J. Lynch Party Republican Democratic Popular vote 52,200 40,823 Percentage 55.50% 43.41% Governor before election John G. Townsend Jr. Republican Elected Governor William D. Denney Republican Elections in Delaware Federal government Presidential elections 1788-89 1792 1796 1800 1804 1808 1812 ...
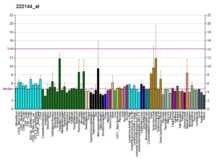
KIF17 المعرفات الأسماء المستعارة KIF17, Kif17, 5930435E01Rik, AW492270, Kif17b, mKIAA1405, KIF3X, KLP-2, OSM-3, kinesin family member 17 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 605037 HomoloGene: 5883 GeneCards: 57576 علم الوجود الجيني الوظيفة الجزيئية • nucleotide binding• microtubule motor activity• microtubule binding• plus-end-directed microtubule motor activity• ATP b...

Multi-period sanctuary and archaeological site This article is about ancient site. For 19th century fortification, see Fort Tas-Silġ. Tas-SilġPart of the late ruins at Tas-SilġShown within MaltaAlternative nameTa' BerikkaLocationŻejtun[1]/Marsaxlokk, MaltaCoordinates35°50′45.3″N 14°33′7.5″E / 35.845917°N 14.552083°E / 35.845917; 14.552083TypeTempleVillageMonasteryFortificationPart ofMegalithic Temples of MaltaHistoryMaterialLimestoneFo...

Valdesamariocomune Valdesamario – Veduta LocalizzazioneStato Spagna Comunità autonoma Castiglia e León Provincia León TerritorioCoordinate42°43′15.96″N 5°57′07.92″W / 42.7211°N 5.9522°W42.7211; -5.9522 (Valdesamario)Coordinate: 42°43′15.96″N 5°57′07.92″W / 42.7211°N 5.9522°W42.7211; -5.9522 (Valdesamario) Altitudine1 022 m s.l.m. Superficie61,73 km² Abitanti255 (2001) Densità4,13 ab./km² Altr...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يونيو 2022) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...

Family of flowering plants PicrodendraceaeTemporal range: Paleocene - recent[1] PreꞒ Ꞓ O S D C P T J K Pg N Tetracoccus dioicus Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Malpighiales Family: PicrodendraceaeSmall[2] Tribes Caletieae Picrodendreae Podocalyceae Picrodendraceae is a family of flowering plants, consisting of 80 species in 24 genera.[3] These are subtropical to tropical and fou...









![{\displaystyle {\sqrt[{n}]{t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01dccfee2c48ba22f0ff3cf344cb0b538760c117)



























