Многочлены Гегенбауэра
| |||||||||||||||||||
Read other articles:

Ilimandiri LarantukaTana NagiLamakéra [1]1600–1904Ibu kotaLarantukaBahasa yang umum digunakanBahasa resmi: Portugis Lainnya: Melayu LarantukaLi'oAgama KatolikPemerintahanMonarkiLorenzo I Sejarah • Didirikan 1600• Dibeli Belanda dari Portugal 1859• Dibubarkan oleh Belanda 1904 Didahului oleh Digantikan oleh krjKerajaan Portugal Hindia Belanda Sekarang bagian dari Indonesia Sunting kotak info • Lihat • BicaraBantuan penggunaan te...

Disambiguazione – Giaggiolo rimanda qui. Se stai cercando il castello nei pressi di Forlì, vedi Castello di Giaggiolo. Questa voce o sezione sull'argomento piante non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Come leggere il tassoboxIris Iris × germanicaUn'Iris gialla e viola davanti a una p...

Pour les articles homonymes, voir MP. Classe préparatoire mathématiques et physique Certification du ministère de l'Enseignement supérieur garantissant son contrôle. Lieu France Établissements Lycée général en CPGE Sélection Diplôme ou concours requis diplôme (Baccalauréat général) Niveau ougrade requis niveau 4 RNCP/CEC Diplôme Durée de la formation 2 ans ou 1 an (prépa ATS) Diplôme délivré Aucun Niveau délivré Aucun Grade délivré Aucun Débouchés Diplômes accessi...

العلاقات الإريترية الشمال مقدونية إريتريا شمال مقدونيا إريتريا شمال مقدونيا تعديل مصدري - تعديل العلاقات الإريترية الشمال مقدونية هي العلاقات الثنائية التي تجمع بين إريتريا وشمال مقدونيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة...

Part of a series onEthnicity in Toronto Aboriginals Black Cambodians Chinese Filipinos French Greeks South Asians Italians Japanese Jews Vietnamese vte Italian Canadians as percent of population by census subdivision Toronto has a large Italian Canadian community, with 30.3 per cent of the ethnic Italians in Canada living in the Greater Toronto Area (GTA) as of 2021.[1] Toronto is home to the fourth largest population of people of Italian descent after Buenos Aires, São Paulo and New...

Pieter de CarpentierPortrait of Pieter de Carpentier by an unknown artist. Rijksmuseum, Amsterdam.5th Governor-General of the Dutch East IndiesIn office1 February 1623 – 30 September 1627Preceded byJan Pieterszoon CoenSucceeded byJan Pieterszoon Coen Personal detailsBorn(1586-02-19)19 February 1586Antwerp, Spanish NetherlandsDied5 September 1659(1659-09-05) (aged 73)Amsterdam, Dutch Republic Pieter de Carpentier (19 February 1586 – 5 September 1659) was a Dutch administ...

Standup comedian character Not to be confused with Neil Burger. Fictional character Neil HamburgerTurkington performing as Hamburger in 2016First appearanceGreat Phone Calls Featuring Neil Hamburger (1992)Created byGregg TurkingtonPortrayed byGregg TurkingtonIn-universe informationOccupationStandup comediansingerGenresAnti-comedypopular musicWebsiteamericasfunnyman.com Neil Hamburger is a standup comedian and singer character created and portrayed by American entertainer Gregg Turkington. Dis...

Disambiguazione – Se stai cercando la medesima competizione per altri sport, vedi Coppa Libertadores 2019 (disambigua). Copa Libertadores 2019Copa Libertadores de América 2019 Competizione Coppa Libertadores Sport Calcio Edizione 60ª Organizzatore CONMEBOL Date dal 22 gennaio 2019al 23 novembre 2019 Partecipanti 47 Nazioni 10 Sede finale Estadio Monumental (Lima) Risultati Vincitore Flamengo(2º titolo) Secondo River Plate Semi-finalisti Boca Juniors Grêmi...

Antichristus,[1] sebuah cukil kayu karya Lucas Cranach si Tua, tentang Sri Paus yang memakai kekuasaan temporal untuk memberikan otoritas besar kepada seorang penguasa yang berkontribusi kepada Gereja Katolik Quid pro quo ('apa untuk apa' dalam bahasa Latin[2]) adalah sebuah frase Latin yang dipakai dalam bahasa Inggris untuk mengartikan pertukaran barang atau jasa, yang diberikan oleh suatu pihak kepada pihak lainnya. Frase-frase dengan pengartian serupa meliputi: beri dan am...

Гленгэрри Солдат Шотландского королевского полка в гленгэрри на параде Гле́нгарри, гле́нгэрри (англ. Glengarry cap, Glengarry hat) — шотландский национальный головной убор, сплюснутая с боков шапочка наподобие пилотки из плотной шерстяной ткани с ленточками сзади. Содержание ...

67th season of the ARCA Menards Series 2019 ARCA Menards Series Previous 2018 Next 2020 Christian Eckes, the 2019 ARCA Menards Series champion. Michael Self finished second behind Eckes in the championship by just 25 points. Bret Holmes finished third in the championship. The 2019 ARCA Menards Series was the 67th season of the ARCA Menards Series. Christian Eckes of Venturini Motorsports won the championship over teammate Michael Self. Eckes became the first champion since Tim Steele in 1997 ...

此條目需要擴充。 (2015年11月27日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 卡洛斯·梅内姆阿根廷總統府官方照片第47任阿根廷總統任期1989年7月8日—1999年12月10日副总统爱德华多·杜阿尔德卡洛斯·鲁考夫(英语:Carlos Ruckauf)前任劳尔·阿方辛 个人资料出生(1930-07-02)1930年7月2日 阿根廷拉里奥哈省阿尼利亚�...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Rural locality in Dnipropetrovsk Oblast, Ukraine Rural settlement in Dnipropetrovsk Oblast, UkraineSlobozhanske СлобожанськеRural settlementSlobozhanske FlagSealSlobozhanskeShow map of UkraineSlobozhanskeShow map of Dnipropetrovsk OblastCoordinates: 48°32′1″N 35°4′41″E / 48.53361°N 35.07806°E / 48.53361; 35.07806CountryUkraineOblastDnipropetrovsk OblastRaionDnipro RaionHromadaSlobozhanske settlement hromada, Dnipropetrovsk OblastEstablished1987F...

Mid-range Android smartphone from Samsung Not to be confused with Samsung Galaxy A51. Samsung Galaxy M51BrandSamsungManufacturerSamsung ElectronicsSeriesSamsung Galaxy M seriesModelSM-M515F/DSNFirst releasedAugust 31, 2020; 3 years ago (2020-08-31)Availability by regionSeptember 11, 2020 (2020-09-11)SuccessorSamsung Galaxy M52 5GRelated Samsung Galaxy M31 Samsung Galaxy A51 TypePhabletDimensions163.9 mm (6.45 in) H 76.3 mm (3.00 in) W 9.5&#...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 新くまのプーさん – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2013年4月) ポータル ディズニー 『新くまのプ...
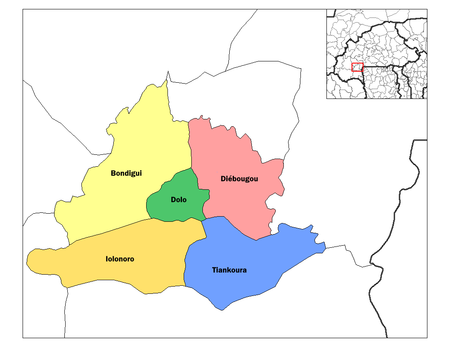
BougouribaProvinsiLetak di Burkina FasoKoordinat: 10°50′N 3°25′W / 10.833°N 3.417°W / 10.833; -3.417Koordinat: 10°50′N 3°25′W / 10.833°N 3.417°W / 10.833; -3.417Negara Burkina FasoRegionRegion Sud-OuestIbu kotaDiébougouLuas • Total1,086 sq mi (2.812 km2)Populasi (2006) • Total102.507Zona waktuUTC+0 (GMT 0) Provinsi Bougouriba adalah sebuah provinsi di Burkina Faso dan di Region Su...

Food product made from milk Milk products and production relationships Dairy products or milk products, also known as lacticinia, are food products made from (or containing) milk.[a][1] The most common dairy animals are cow, water buffalo, nanny goat, and ewe. Dairy products include common grocery store food around the world such as yogurt, cheese, milk and butter.[2][3] A facility that produces dairy products is a dairy.[b][4] Dairy products ar...

Questa voce sull'argomento ginnasti norvegesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Harald HalvorsenNazionalità Norvegia Ginnastica artistica Palmarès Competizione Ori Argenti Bronzi Giochi olimpici 0 1 0 Giochi olimpici intermedi 1 0 0 Vedi maggiori dettagliIl simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Harald Halvorsen (16 novembre 1878 – 11 agosto 1965) è stato un ginnasta no...

Indian political party Political party in India Indian Union Dalit League LeaderU. C. Raman, A. P. Unnikrishnan[1][2]FounderU. C. RamanHeadquartersKozhikkode, Kerala, IndiaAllianceIndian Union Muslim LeagueUDFPolitics of IndiaPolitical partiesElections Dalit League is also known as Indian Union Dalit League (IUDL)[3] Indian Political Party and Caste wing of the Indian Union Muslim League[4] in Kerala, India. It was founded by IUML and A. P. Unnikrishnan, U...


![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![{\displaystyle \|C_{n}^{(\alpha )}(z)\|^{2}={\frac {2^{1-2\alpha }\pi \Gamma (n+2\alpha )}{n!(n+\alpha )[\Gamma (\alpha )]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e23d8d92fa7d947e3b8ba165829e31d1e617b247)
















![{\displaystyle C_{n}^{(\alpha )}(z)={\frac {1}{n}}[2z(n+\alpha -1)C_{n-1}^{(\alpha )}(z)-(n+2\alpha -2)C_{n-2}^{(\alpha )}(z)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/841d1c8bfe0bec94c1321f5b637b48374d0a086b)








![{\displaystyle C_{n}^{(\alpha )}(z)={\frac {(-2)^{n}}{n!}}{\frac {\Gamma (n+\alpha )\Gamma (n+2\alpha )}{\Gamma (\alpha )\Gamma (2n+2\alpha )}}(1-z^{2})^{-\alpha +1/2}{\frac {{\rm {d}}^{n}}{{\rm {d}}z^{n}}}\left[(1-z^{2})^{n+\alpha -1/2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b93171c899e4b1b8bcfd109e83dcffefe565ef48)


![{\displaystyle \int _{-1}^{1}\left[C_{n}^{(\alpha )}(z)\right]^{2}(1-z^{2})^{\alpha -1/2}\,{\rm {d}}z={\frac {2^{1-2\alpha }\pi \Gamma (n+2\alpha )}{n!(n+\alpha )[\Gamma (\alpha )]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c977fddb9c67cf4b354ac2c6be13f4a859eaa9ee)



![{\displaystyle {\rm {Re}}\left[C_{n}^{(\alpha )}(x+{\rm {i}}y)\right]=\sum _{k=0}^{\lfloor n/2\rfloor }{\frac {(-1)^{k}2^{2k}(\alpha )_{2k}}{(2k)!}}\;C_{n-2k}^{(2k+\alpha )}(x)\;y^{2k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/901c534ac4529d499c7c795aad6a4edc6fdfbfab)
![{\displaystyle {\rm {Im}}\left[C_{n}^{(\alpha )}(x+{\rm {i}}y)\right]=\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {(-1)^{k}2^{2k+1}(\alpha )_{2k+1}}{(2k+1)!}}\;C_{n-2k-1}^{(2k+\alpha +1)}(x)\;y^{2k+1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/267631aba1a0bd0fcb874e6ca02fc84e4152cd7e)