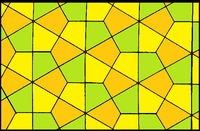
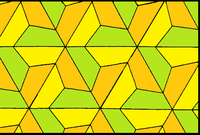
Pavare trihexagonală romboidală
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (April 2014) (Learn how and when to remove this template message) Navi Mumbai skyline This list of the tallest buildings in Navi Mumbai ranks high-rise buildings and skyscrapers in Navi Mumbai, Maharashtra, India. Navi Mumbai is a planned township of Mumbai on the west coast of the Indian state of Maharas...

PT Bosowa CorporindoNama dagangBosowa CorpIndustriKonglomeratDidirikan22 Februari 1973PendiriAksa MahmudKantorpusatJakarta:Jl. H.R. Rasuna Said Kav. 1-2, Kuningan, Setiabudi, Jakarta Selatan, IndonesiaMakassar:Jl. Ahmad Yani, Pisang Utara, Ujung Pandang, Makassar, IndonesiaWilayah operasiNasionalProdukOtomotif, semen, logistik, pertambangan, properti, jasa keuangan, infrastruktur, energi, media, dan lainnyaSitus webwww.bosowa.co.id Bosowa Corp adalah perusahaan induk (holding company) yang me...

Kanbawza BankJenisSwastaIndustriPerbankanDidirikan1994KantorpusatYangon, MyanmarTokohkunciAung Ko Win (Ketua Emeritus)ProdukJasa keuanganKaryawanLebih dari 18.000Situs webwww.kbzbank.com Kanbawza Bank (Burma: ကမ္ဘောဇဘဏ်code: my is deprecated ; disingkat KBZ Bank) adalah sebuah bank komersial swasta di Myanmar. Bank tersebut didirikan pada 1 Juli 1994 di Taunggyi, Negara Bagian Shan. KBZ Bank memiliki merek yang sama dengan sejumlah perusahaan di Myanmar namun terpisah dan ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Setidaknya 37 spesies amfibi asli Taiwan .[1][2] Dari jumlah tersebut, 17 spesies endemik Taiwan. Salamander Echinotriton andersoni dianggap punah di Taiwan (tetapi bertahan di Kepulauan Ryukyu Jepang). Selain itu, ada tiga spesies yan...

Israeli former football club Football clubHapoel Katamon JerusalemFull nameHapoel Katamon Jerusalem F.C.Nickname(s)Katamon, The Red Devils, HapoelFounded2007 (as Hapoel Katamon/Mevasseret Zion),2009 (as Hapoel Katamon Jerusalem)2020 (as Hapoel Jerusalem)Dissolved2020 Home colours Away colours Third colours Hapoel Katamon Jerusalem F.C. (Hebrew: הפועל קטמון ירושלים) was the name of the club that is currently called Hapoel Jerusalem, an Israeli fan-owned association football cl...

1947 filmIn the Name of LifeDirected byIosif KheifitsAleksandr ZarkhiWritten byYevgeni GabrilovichSergei YermolinskyIosif KheifitsAleksandr ZarkhiStarringViktor KhokhryakovMikhail KuznetsovOleg ZhakovKlavdiya LepanovaCinematographyVyacheslav GordanovMusic byVenedikt PushkovProductioncompanyLenfilm StudioDistributed bySovexportRelease date 1947 (1947) Running time101 minutesCountrySoviet UnionLanguageRussian In the Name of Life (Russian: Во имя жизни, romanized: Vo imya zhi...

American politician (1756–1805) Uriah ForrestMember of the U.S. House of Representativesfrom Maryland's 3rd districtIn officeMarch 4, 1793 – November 8, 1794Preceded byJohn F. MercerSucceeded byBenjamin Edwards Personal detailsBorn1756 (1756)St. Mary's County, Province of Maryland, British AmericaDiedJuly 6, 1805(1805-07-06) (aged 48–49)Washington, D.C., U.S.Resting placeOak Hill CemeteryWashington, D.C., U.S.Political partyFederalistSpouseRebecca PlaterRe...

Bagian dari seri tentangBudaya Indonesia Sejarah Sejarah menurut provinsi Bangsa Daftar suku bangsa Daftar suku bangsa menurut provinsi Bahasa Bahasa Indonesia Tradisi Etiket di Indonesia Busana nasional Indonesia Mitologi dan cerita rakyat Mitologi Cerita rakyat Hidangan Hari raya Festival Hari libur nasional Agama Islam Kekristenan Katolik Protestan Hindu Buddhisme Konghucu Yahudi Kepercayaan Seni Arsitektur Tarian Sastra Musik dan seni pertunjukan Musik Media Televisi Perfilman Olahraga Bo...

Cristiana Carlotta di Württemberg-WinnentalMargravia di Brandeburgo-AnsbachIn carica28 agosto 1709 – 7 gennaio 1723 NascitaKirchheim unter Teck, 20 agosto 1694 MorteAnsbach, 25 dicembre 1729 Casa realeCasato del Württemberg PadreFederico Carlo di Württemberg-Winnental MadreEleonora Giuliana di Brandeburgo-Ansbach Consorte diGuglielmo Federico, margravio di Brandeburgo-Ansbach FigliCarlo Guglielmo Federico, margravio di Brandeburgo-Ansbach Cristiana Carlotta di Württemberg-Winnenta...

Self-designation used by ancient Indo-Iranian peoples This article is about the cultural and historical concept. For other uses, see Aryan (disambiguation). Part of a series onIndo-European topics Languages List of Indo-European languages Extant Albanoid Albanian Armenian Balto-Slavic Baltic Slavic Celtic Germanic Hellenic Greek Kurdish Indo-Iranian Indo-Aryan Iranian Nuristani Italic Romance Extinct Anatolian Tocharian Paleo-Balkan Dacian Illyrian Liburnian Messapic Mysian Paeonian Phrygian ...

Uktena redirects here. For the tribe of werewolves in the World of Darkness setting, see Uktena (World of Darkness). Mythological serpent found in the mythology of many cultures The Horned Serpent design is a common theme on pottery from Casas Grandes (Paquimé) A Horned Serpent in a Barrier Canyon Style pictograph, Western San Rafael Swell region of Utah. The Horned Serpent appears in the mythologies of many cultures including Native American peoples,[1] European, and Near Eastern my...

Kashima Antlers 1998 football seasonKashima Antlers1998 seasonManagerJoão CarlosTakashi SekizukaZé MárioStadiumKashima Soccer StadiumJ.LeagueChampionsEmperor's CupSemifinalsJ.League CupSemifinalsTop goalscorerAtsushi Yanagisawa (22) Home colours Away colours ← 19971999 → 1998 Kashima Antlers season Competitions Competitions Position J.League Champions / 18 clubs Emperor's Cup Semifinals J.League Cup Semifinals Domestic results J.League Kashima Antlers v Avispa Fukuoka...

弗雷德里克·齊盧巴Frederick Chiluba第2任赞比亚总统任期1991年11月2日—2002年1月2日副职利维·姆瓦纳瓦萨前任肯尼思·卡翁达继任利维·姆瓦纳瓦萨 个人资料出生(1943-04-30)1943年4月30日北罗得西亚基特韦逝世2011年6月18日(2011歲—06—18)(68歲) 尚比亞卢萨卡(Lusaka)墓地 尚比亞卢萨卡使館公園總統陵園(英语:Embassy Park Presidential Burial)国籍赞比亚政党多黨民主運動(MMD)...

Final Piala FA 2008TurnamenPiala FA 2007–2008 Cardiff City Portsmouth 0 1 Tanggal17 Mei 2008StadionStadion Wembley, LondonWasitMike Dean[1]Penonton89.874← 2007 2009 → Final Piala FA 2008 adalah pertandingan sepak bola antara Portsmouth dan tim Wales Cardiff City yang diselenggarakan pada 17 Mei 2008 di Stadion Wembley, London. Pertandingan ini merupakan pertandingan final ke-127 Piala FA sebagai pertandingan penentu pemenang musim 2007–2008. Pertandingan ini dimenangka...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (فبراير 2023) الحدثكأس المملكة المتحدة 1874–75 نادي كوينز بارك Renton F.C. [الإنجليزية] 3 0 ال�...

Untuk bidang ilmiah, lihat hukum (ilmiah). Bagian dari seriIlmu Pengetahuan Formal Logika Matematika Logika matematika Statistika matematika Ilmu komputer teoretis Teori permainan Teori keputusan Ilmu aktuaria Teori informasi Teori sistem FisikalFisika Fisika klasik Fisika modern Fisika terapan Fisika komputasi Fisika atom Fisika nuklir Fisika partikel Fisika eksperimental Fisika teori Fisika benda terkondensasi Mekanika Mekanika klasik Mekanika kuantum Mekanika kontinuum Rheologi Mekanika be...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2014 Uva Provincial Council election – news · newspapers · books · scholar · JSTOR (February 2024) (Learn how and when to remove this message) 6th Sri Lankan provincial council election in Uva Province ← 2014 (Mar) 20 September 2014 34 seats across o...

Empress of Japan from 1989 to 2019 You can help expand this article with text translated from the corresponding article in Japanese. (June 2021) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate t...

提示:此条目页的主题不是努瓦图。 萬那杜共和國Ripablik blong Vanuatu(比斯拉馬語)République de Vanuatu(法語)Republic of Vanuatu(英語) 国旗 国徽 格言:Long God yumi stanap (比斯拉马语)“让我们坚定的与主站在一起”国歌:Yumi, Yumi, Yumi(我們、我們、我們)首都暨最大城市維拉港官方语言英語、法語、比斯拉馬語官方文字拉丁字母族群萬那杜人宗教基督教政...