Pavare rombică
| |||||||||||||||||||||
Read other articles:

It has been suggested that this article be merged into List of Swedish films of the 2010s. (Discuss) Proposed since August 2023. 2014 saw the death of Malik Bendjelloul. The Swedish film industry produced over six hundred feature films in 2014. This article fully lists all non-pornographic films, including short films, that had a release date in that year and which were at least partly made by the Sweden. It does not include films first released in previous years that had release dates in 20...

RacletteNegara asalSwiss, PrancisWilayahAlpenSumber susuSapiDipasteurisasiYaTeksturKerasKadar lemak45%Waktu pematangan3 bulan[1] Raclette adalah keju yang berasal dari Wallis di Swiss dan Savoie di Prancis dan dibuat dari susu sapi yang dipasteurisasi.[1][2] Nama keju ini berasal dari kata racler yang dalam bahasa Prancis berarti menggores atau mengerik.[1] Pada zaman pertengahan, para gembala dari Swiss senang dengan keju Raclette yang pedas.[1] Mereka...

BinuangKecamatanKantor kecamatan BinuangPeta lokasi Kecamatan BinuangNegara IndonesiaProvinsiKalimantan SelatanKabupatenTapinPemerintahan • CamatEko Haryono, SE, MMPopulasi (2023) • Total32,536 jiwa • Kepadatan79,80/km2 (206,7/sq mi)Kode Kemendagri63.05.01 Kode BPS6305010 Luas342,08 km²Desa/kelurahan8/3 Binuang adalah kecamatan di Kabupaten Tapin, Kalimantan Selatan, Indonesia. Binuang merupakan kecamatan dengan jumlah penduduk terbanyak di ...

Im Chang-jungLahir30 November 1973 (umur 50)Icheon, Gyeonggi Province, South KoreaNama lainLim/Yim Chang-jungPendidikanChungAng University[1]Theater and FilmPekerjaanAktor, penyanyiTahun aktif1990–sekarangSuami/istripro golfer Kim Hyun-joo (2006–2013)[2][3]Anak5 putraNama KoreaHangul임창정 Hanja任昌丁 Alih AksaraIm Chang-jeongMcCune–ReischauerIm Ch'ang-chŏng Im Chang-jung (lahir 30 November 1973) adalah aktor dan penyanyi asal Korea Selatan...

Upaya aksesi Uni Eropa Kroasia Rata-rata anggota Uni Eropa Kroasia PPP GDP ($Juta) 552.780 80,334 Luas (km2) 165.048 56,594 Populasi 18.583.598 4.284.889 StatusAnggota Jumlah bab dibuka: 33[1] Jumlah bab ditutup: 33[2] Situsmvep.hr Kroasia resmi menjadi negara anggota Uni Eropa yang ke-28 pada tanggal 1 Juli 2013. Kroasia mengajukan permohonan untuk keanggotaan Uni Eropa pada tahun 2003 dan Komisi Eropa merekomendasikan untuk menjadikannya sebagai kandidat...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

William Bellinger Bulloch Fonctions Sénateur des États-Unispour la Géorgie 8 avril – 6 novembre 1813(6 mois et 29 jours) Prédécesseur William Harris Crawford Successeur William Wyatt Bibb Maire de Savannah 1809 – 1812(3 ans) Biographie Date de naissance 1777 Lieu de naissance Savannah (Géorgie, États-Unis) Date de décès 6 mai 1852 Lieu de décès Savannah (Géorgie, États-Unis) Nationalité Américaine modifier William Bellinger Bulloch (1777, Savannah - 6 ...

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

关于浙江省的2019冠状病毒病疫情情况,请见「2019冠狀病毒病浙江省疫情」。 维基百科中的醫學内容仅供参考,並不能視作專業意見。如需獲取醫療幫助或意見,请咨询专业人士。詳見醫學聲明。 在這條目內未有標明年份的日期都代表是2022年。 若非特別註明,本條目所有時間皆為東八區標準時間(UTC+8)。 2022年3月杭州四季青服装市场2019冠状病毒病聚集性疫�...

The neutrality of the style of writing in this article is disputed. Please do not remove this message until conditions to do so are met. (March 2023) (Learn how and when to remove this message) Józef MackiewiczMackiewicz in Wilno; before 1939Born(1902-04-01)1 April 1902Saint PetersburgDied31 January 1985(1985-01-31) (aged 82)MunichOccupationNovelistNationalityPolishSignature Józef Mackiewicz (1 April 1902 – 31 January 1985) was a Polish writer, novelist and political commentator; bes...

الزوج المتشرد الزوج المتشرد تاريخ الصدور 1960 مدة العرض 100 دقيقة البلد الجمهورية العربية المتحدة اللغة الأصلية العربية الطاقم المخرج حسن الصيفي الإنتاج كامل الحفناوي الكاتب صبري عزت البطولة أحمد رمزينعيمة عاكفزهرة العلاحسين رياضتوفيق الدقن موسيقى علي إسماعيل صناعة سي...

Iranian refugee (1945–2022) Mehran Karimi Nasseriمهران کریمی ناصریNasseri in 2005Born1945 (1945)[1]Masjed Soleiman, Imperial State of IranDied12 November 2022(2022-11-12) (aged 77)Charles de Gaulle Airport, Le Mesnil-Amelot, FranceOther namesSir, Alfred MehranCitizenshipIran (until 1977)Stateless (from 1977) Mehran Karimi Nasseri (Persian: مهران کریمی ناصری, pronounced [mehˈrɒn kæriˈmi nɒseˈri]; 1945 – 12 November 2022), a...

This article is about the Streltsy uprising of 1698. For the Streltsy uprising of 1682, see Moscow uprising of 1682. Streltsy uprisingThe Morning of the Streltsy Execution, by Vasily Surikov, 1881Native name Стрелецкий бунтDate1698Location Tsardom of RussiaCauseMilitary-service hardships as one of the possible causesOutcomeSuppression of the uprising The Streltsy uprising of 1698 (Russian: Стрелецкий бунт 1698 года) was an uprising of the Moscow Strel...

Bayer 04 LeverkusenCalcio Campione di Germania in carica Detentore della Coppa di Germania Werkself (squadra della fabbrica),[1] Die Aspirin (le aspirine), Pillendreher (i prendipillole)[2] Segni distintiviUniformi di gara Casa Trasferta Terza divisa Colori sociali Rosso, nero SimboliLeone InnoBayer 04 Leverkusen Hymne Dati societariCittàLeverkusen Nazione Germania ConfederazioneUEFA Federazione DFB CampionatoBundesliga Fondazione1904 Proprietario Bayer Presidente Fernan...

Board wargame published in 1972 Cover of 1st edition, 1972 Quebec 1759 is a board wargame published in 1972 by Gamma Two Games (now Columbia Games) that simulates the Battle of the Plains of Abraham outside the walls of Quebec in 1759. The game uses wooden blocks set on their edge rather than the more traditional cardboard counters, unique for a wargame in 1972. Background In 1759, as part of the French and Indian War, British general James Wolfe, using British soldiers and elements of the Ro...

British philosopher and logician (1872–1970) The Right HonourableThe Earl RussellOM FRSRussell in 1949BornBertrand Arthur William Russell(1872-05-18)18 May 1872Trellech, Monmouthshire, Wales[a]Died2 February 1970(1970-02-02) (aged 97)Penrhyndeudraeth, Merionethshire, WalesEducationTrinity College, Cambridge (BA, 1893)Spouses Alys Pearsall Smith (m. 1894; div. 1921) Dora Black (m. 1921; d...

Italian Jesuit cardinal and saint (1542–1621) SaintRobert BellarmineSJCardinal, Archbishop Emeritus of Capua17th-century portrait of Robert Bellarmine, Antwerp, Museum Plantin-MoretusChurchCatholic ChurchArchdioceseCapuaAppointed18 March 1602Installed21 April 1602Term endedAugust 1605PredecessorCesare CostaSuccessorAntonio Caetani Jr.Other post(s)Cardinal-Priest of Santa PrassedeOrdersOrdination19 March 1570Consecration21 April 1602by Clement VIIICreated cardinal3 March 1599by Clement ...
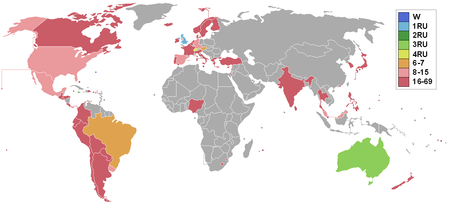
Bài này không có nguồn tham khảo nào. Mời bạn giúp cải thiện bài bằng cách bổ sung các nguồn tham khảo đáng tin cậy. Các nội dung không có nguồn có thể bị nghi ngờ và xóa bỏ. Nếu bài được dịch từ Wikipedia ngôn ngữ khác thì bạn có thể chép nguồn tham khảo bên đó sang đây. (tháng 12/2021) Hoa hậu Thế giới 1979Ngày15 tháng 11 năm 1979Dẫn chương trìnhSacha Distel và Esther RantzenĐịa điểmHội...

1999 studio album by Mournful CongregationTears from a Grieving HeartStudio album by Mournful CongregationReleased1999 (original), September 12, 2012 (CD)Recorded1997–98GenreFuneral doom metalLength45:07LabelIndependentProducerMournful Congregation, Steve FieldhouseMournful Congregation chronology An Epic Dream of Desire (demo)(1995) Tears from a Grieving Heart(1999) The Dawning of Mournful Hymns (compilation) Tears from a Grieving Heart is the debut studio album by the Australian ...

1950 novel by Agatha Christie A Murder Is Announced Dust-jacket illustration of the first UK editionAuthorAgatha ChristieLanguageEnglishGenreCrime novelPublisherCollins Crime ClubPublication dateJune 1950Publication placeUnited KingdomPages256 (first edition, hardcover)Preceded byCrooked House (publication)The Moving Finger (series) Followed byThree Blind Mice and Other Stories (publication)A Pocket Full of Rye (series) A Murder Is Announced is a work of detective fiction...












