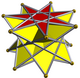
正七芒星、円周を7等分し、2個隣の点どうしをつないで作られる事からシュレーフリ記号 は{7/2}で表される。 正七芒星、円周を7等分し、3個隣の点どうしをつないで作られる事からシュレーフリ記号 は{7/3}で表される。 幾何学において、七芒星 (しちぼうせい)、ヘプタグラム (英語:heptagram, septagram, septegram、septogram)は、7つの角を持つ星型多角形 である。
heptagramは、ギリシャ語 の倍数接頭辞 で7を意味する hepta- と、「線」を意味するギリシャ語γραμμή (grammḗ )から来た接尾辞 -gram [ 1]
七芒星は既約分数で2つの形式で描画できる最小の星型正多角形 である。2つの七芒星は、heptagram ({7/2}の場合)およびgreat heptagram ({7/3}の場合)と呼ばれることもある。
より小さいものでは六芒星 {6/2}は2つの三角形の複合体である。 最小の星形多角形は五芒星 {5/2}である。
より大きいものでは、八芒星 が{8/3}と2つの正方形の複合体である{8/2}。そして九芒星 の{9/2}、{9/4}、および3つの三角形の複合物である{9/3}と続く。
角柱 (7/2)
角柱 (7/3)
完全グラフ
宗教・オカルト 他、錬金術やイスラム教 の聖典クルアーン にも登場する。
その他
^ γραμμή , Henry George Liddell, Robert Scott, A Greek-English Lexicon , on Perseus
Grünbaum, B. and G.C. Shephard; Tilings and Patterns , New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1 .Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993) , ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)非古典的 (2辺以下) 辺の数: 3–10
辺の数: 11–20 辺の数: 21–30 辺の数: 31–40 辺の数: 41–50 辺の数: 51–70 辺の数: 71–100 辺の数: 101– 無限 星型多角形 多角形のクラス