O-grande
|
Read other articles:

1922 novel by Rafael Sabatini Captain Blood: His Odyssey 1922 dust jacket coverAuthorRafael SabatiniCountryEnglandLanguageEnglishSubjectPiracy, justicePublisherHoughton Mifflin CompanyPublication date1922 Captain Blood: His Odyssey is an adventure novel by Rafael Sabatini, originally published in 1922. Development Sabatini was a proponent of basing historical fiction as closely as possible on history. Although Blood is a fictional character, much of the historical background of the novel is ...
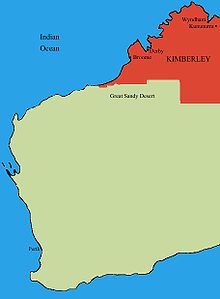
Kimberley adalah wilayah paling utara dari sembilan wilayah di Australia Barat. Di barat berbatasan dengan Samudera Hindia, di utara dengan Laut Timor, di selatan dengan Gurun Pasir Besar dan Tanami di wilayah Pilbara, dan di timur dengan Northern Territory. Wilayah ini dinamai pada tahun 1879 oleh surveyor pemerintah Alexander Forrest setelah Menteri Negara Koloni John Wodehouse, Earl of Kimberley ke-1. [1][2] Lihat pula Australia Barat Australia Samudra Hindia Laut Timor Ref...

2023 film score by Michael AbelsThe Burial (Amazon Original Motion Picture Score)Film score by Michael AbelsReleasedOctober 6, 2023GenreFilm scoreLength34:58LabelAmazon Content ServicesProducerMichael AbelsMichael Abels chronology Landscape with Invisible Hand(2023) The Burial(2023) The Burial (Amazon Original Motion Picture Score) is the score album to the 2023 film of the same name directed by Maggie Betts and starred Tommy Lee Jones and Jamie Foxx. Featuring musical score by Micha...

QinnasrinArab: قنسرينcode: ar is deprecated Lokasi di SyriaLokasiSyriaWilayahKegubernuran AleppoKoordinat35°59′55″N 36°59′53″E / 35.998611°N 36.998056°E / 35.998611; 36.998056 Qinnasrin ( قنسرين; bahasa Suryani: ܩܢܫܪܝܢ, Qinnašrīn; yang berarti Sarang Elang),[1] juga dikenal dengan berbagai romanisasi[n 1] dan awalnya dikenal sebagai Chalcis-on-Belus (bahasa Latin: Chalcis ad Belum;[2] Yunani: Χαλκὶς...

Cet article est une ébauche concernant une localité slovaque. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Podbrezová Administration Pays Slovaquie Région Banská Bystrica District Brezno Statut Village Starosta (maire) Mandat Ladislav Kardhordó (Indépendant) mandat : 2018-2022 Code postal 976 81 Plaqueminéralogique BR Code LAU 2 508853 Démographie Population 3 860 hab. (31 déc. 2018) ...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

بن ستيلر Ben Stiller بن ستيلر في عام 2019 معلومات شخصية اسم الولادة بنجامين إدوارد ستيلر الميلاد 30 نوفمبر 1965 (العمر 58 سنة)مدينة نيويورك، نيويوركالولايات المتحدة الأمريكية مواطنة الولايات المتحدة استعمال اليد أعسر الديانة اليهودية عضو في نقابة الكتاب الأمريكية الشرقية ...

AnuketDewi Anuket, digambarkan sebagai seorang wanita dengan hiasan kepala yang tinggi dan berbuluHieroglif Pusat pemujaanElefantin, Pulau SehelSimbolBusur, anak panah, kijang, bulu burung untaOrang tuaKhnum dan Satis Anuket adalah dewi Mesir kuno dari Riam Sungai Nil dan Nubia Hilir pada umumnya, disembah terutama di Elefantin dekat Riam Pertama.[1] Etimologi Dalam bahasa Mesir kuno, dia dikenal sebagai Anuket, Anaka,[2] atau Anqet.[3] Namanya berarti Penggenggam atau...

Diagram kestabilan isotop. Dalam fisika nuklir, bilangan ajaib adalah jumlah nukleon (proton atau neutron) yang menghasilkan kulit penuh dalam inti atom sesuai model kulit inti. Dalam model ini, inti atom tersusun dalam berbagai lapisan kulit untuk proton dan untuk neutron, seperti halnya lapisan kulit elektron. Setiap proton dan neutron masing-masing memiliki tingkat energi yang relatif berdekatan, kecuali jika lapisan kulit sebelumnya telah penuh maka proton atau neutron selanjutnya membutu...

أدريانا دورن معلومات شخصية الميلاد 30 ديسمبر 1986 (38 سنة) ماناغوا مواطنة نيكاراغوا الطول 175 سنتيمتر الحياة العملية المدرسة الأم جامعة ولاية بنسلفانيا المهنة عارضة، ومتسابقة ملكة الجمال المواقع الموقع الموقع الرسمي IMDB صفحتها على IMDB تعديل مصد�...

Kerameikos Archaeological Museum The Kerameikos Archaeological Museum is located in Kerameikos, Athens, Greece and was built in 1937. It houses many important early Geometric art pieces that date as far back as 860 BC. It was expanded in the 1960s by the Boehringer brothers of Boehringer Ingelheim fame. Its official address is Ermou, Athens 125, Greece. History In 1863, archaeologists first started housing pottery and other artifacts found in the dig site in a small, makeshift outpost. It was...

United States Air Force numbered unit Fourth Air ForceShield of the Fourth Air ForceActive1 December 1985 - present (as Fourth Air Force)24 September 1976 - 1 December 1985 (as Fourth Air Force (Reserve))20 January 1966 - 30 September 196918 September 1942 - 1 September 1960 (as Fourth Air Force)26 March 1941 - 18 September 1942 (as 4 Air Force)19 October 1940 - 26 March 1941 (as Southwest Air District)(83 years, 7 months)[1]Country United States of AmericaBranch U...

American basketball coach Marynell MeadorsPersonal informationBorn (1943-08-27) August 27, 1943 (age 80)Nashville, Tennessee, U.S.Career informationCollegeMiddle Tennessee StateCoaching career1970–2012Career historyAs coach:1970–1986Tennessee Tech1986–1996Florida State1997–1999Charlotte Sting2003–2005Pittsburgh (assistant)2005–2007Washington Mystics (assistant)2008–2012Atlanta Dream Career highlights and awardsAs coach: WNBA Coach of the Year (2009) Medals Women’s Basketb...

Discontinued SSRI antidepressant drug IndalpineClinical dataTrade namesUpstèneIdentifiers IUPAC name 3-(2-Piperidin-4-ylethyl)-1H-indole CAS Number63758-79-2 YPubChem CID44668DrugBankDB08953 YChemSpider40643 YUNIIV35562QSVTChEMBLChEMBL276520 YCompTox Dashboard (EPA)DTXSID80213196 ECHA InfoCard100.058.569 Chemical and physical dataFormulaC15H20N2Molar mass228.339 g·mol−13D model (JSmol)Interactive image SMILES c2(c1ccccc1[nH]c2)CCC3CCNCC3 InChI InChI=1S/C15H20N2/c1...

Austronesian language spoken in New Caledonia OroweʼÔrôêRegionBourail, New CaledoniaNative speakers490 (2009 census)[1]Language familyAustronesian Malayo-PolynesianOceanicSouthern OceanicNew Caledonian – LoyaltiesNew CaledonianSouthernSouth SouthernWailicOroweLanguage codesISO 639-3bpkGlottologorow1242ELP'ÔrôêOrowe is classified as Definitely Endangered by the UNESCO Atlas of the World's Languages in Danger Orowe (ʼÔrôê, Boewe, Neukaledonien) is an Oceanic ...

2017 studio album by KhalidAmerican TeenStudio album by KhalidReleasedMarch 3, 2017Studio Various Beacon Hill Recording Studio (El Paso, TX)Golden Age (Los Angeles, CA)Body High Studios (Los Angeles, CA)Gower House (Los Angeles, CA)Temple Base Studios (Los Angeles, CA)Black Wax Studio (New York, NY)The Premises (London, United Kingdom)Sony/ATV Studios (London, United Kingdom) GenreR&Bteen popLength54:37LabelRight HandRCAProducerSyk Sense (also exec.)Alfredo GonzalezBryan MedinaDan...

Cet article possède un paronyme, voir Elektron. Vous lisez un « article de qualité » labellisé en 2013. ÉlectronDes expériences menées avec les tubes de Crookes ont démontré avec certitude l'existence de l'électron.Sur la photo, le tube est rempli d'un gaz à basse pression. Une tension électrique élevée est appliquée entre la cathode (à l'extrémité gauche) et l'anode (à l'extrémité du coude sous le tube). À la cathode, cette tension fait naître un faisceau d...

Marzuki Yatim Menteri Urusan Hubungan Pemerintah dengan Alim Ulama Indonesia ke-3Masa jabatan24 Februari 1966 – 25 Juli 1966PresidenSoekarnoMenteriSaifuddin ZuhriPendahuluMuhammad IlyasPenggantiJabatan dihapuskanSekretaris Jenderal Organisasi Islam Asia AfrikaMasa jabatan14 Desember 1965 – Tidak diketahuiKetuaAhmad Syaikhu Informasi pribadiMeninggal25 Mei 1992[butuh rujukan]Jakarta, IndonesiaMakamTaman Pemakaman Umum Tanah KusirPartai politikMasyumiSuami/istr...

この項目では、埼玉県の自治体について説明しています。その他の用法については「川島町 (曖昧さ回避)」をご覧ください。 かわじままち 川島町 遠山記念館 川島町旗 川島町章 国 日本地方 関東地方都道府県 埼玉県郡 比企郡市町村コード 11346-8法人番号 8000020113468 面積 41.63km2総人口 18,385人 [編集](推計人口、2024年9月1日)人口密度 442人/km2隣接自治体 川越市、東�...

ファナック株式会社FANUC CORPORATION 本社・工場群(山梨県忍野村)種類 株式会社機関設計 監査等委員会設置会社[1]市場情報 東証プライム 69541976年11月4日上場 本社所在地 日本〒401-0597山梨県南都留郡忍野村忍草(しぼくさ)字古馬場3580[2]北緯35度26分43.8秒 東経138度50分34.1秒 / 北緯35.445500度 東経138.842806度 / 35.445500; 138.842806座標: 北緯35度26分43....

























































































