Funzione lipschitziana
|
Read other articles:

Karbovanets Ukrainaукраїнський карбованець (Ukraina) 1 karbovanets1,000,000 karbovantsiv ISO 4217KodeUAKDenominasiSubsatuan 1/100kopiyka (копійка)Bentuk jamakkarbovantsi (jamak nominatif), karbovantsiv (jamak genitif) kopiyka (копійка)kopiyky (jamak nominatif), kopiyok (jamak genitif)Uang kertas1, 3, 5, 10, 25, 50, 100, 200, 500, 1000, 2000, 5000, 10 000, 20 000, 50 000, 100 000, 200 000, 500 000, 1 000 00...

Sok Kenal Sok DekatGenre Drama Roman Komedi Remaja PembuatMultivision PlusSkenarioHerry B. ArissaSutradara Vasant R. Patel Vera Flatyer Pemeran Jonathan Frizzy Ananda Faturrahman Hengky Kurniawan Ratu Felisha Nirin Kumpul Cici Tegal Puput Melati Pricilla Camelia Sandra I. Sitanija Subarkah Hadisarjana Boy Tirayoh Negara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode30 (daftar episode)ProduksiProduser eksekutifGobind PunjabiProduserRaam PunjabiPengaturan kameraMulti-kameraD...

الدوري العراقي الممتاز السلسلة دوري نجوم العراق الموسم 2002–03 البلد العراق الفرق 20 الفائز تم إلغاء الدوري بطولة الأندية العربية الموحدة الشرطة دوري أبطال آسيا الشرطةالقوة الجوية دوري أبطال العرب الزوراءالطلبة 2001–02 2003–04 تعديل مصدري - تعديل دوري الدرجة الأو�...

Walpole, difoto oleh Carl Van Vechten, 1934 Sir Hugh Seymour Walpole, CBE (13 Maret 1884 – 1 Juni 1941) adalah seorang novelis Inggris kelahiran Selandia Baru. Ia adalah putra dari biarawan Anglikan Ia adalah penulis dengan penjualan terbaik pada 1920an dan 1930an Biografi Tahun-tahun awal Walpole lahir di Auckland, Selandia Baru, sebagai anak sulung dari tiga bersaudara dari pasangan Rev Somerset Walpole dan istrinya, Mildred Helen, née Barham (1854–1925).[1] Catat...

Pour les articles homonymes, voir Mike Lee. Mike Lee Portrait officiel de Mike Lee (2017). Fonctions Sénateur des États-Unis En fonction depuis le 3 janvier 2011(13 ans, 3 mois et 17 jours) Élection 2 novembre 2010 Réélection 8 novembre 20168 novembre 2022 Circonscription Utah Législature 112e, 113e, 114e, 115e, 116e, 117e et 118e Groupe politique Républicain Prédécesseur Robert Bennett Biographie Nom de naissance Michael Shumway Lee Date de naissance 4 juin 1971 (52&...

Elections in India in 1978 This article is part of a series on the Politics of India Constitution and law Constitution of India Fundamental Rights, Directive Principles and Fundamental Duties of India Human rights Judicial review Taxation Uniform Civil Code Basic structure doctrine Amendment Law of India Indian criminal law Bharatiya Nyaya Sanhita Bharatiya Nagarik Suraksha Sanhita Bharatiya Sakshya Adhiniyam Code of Civil Procedure (India) Government President of India Droupadi Murmu Vice Pr...

Decision making; evaluation of evidence to make a decision Judgment redirects here. For other uses, see Judgment (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may need to be rewritten to comply with Wikipedia's quality standards, as it contains many issues, including first-person point of view, poor organization, some instances of non-neutral point of view...

Schloss Oranienstein in 2008. The Oranienstein Letters are a series of letters sent by William V, Prince of Orange in December 1801 from Schloss Oranienstein near Diez, Germany. William addressed them to 15 Orangist ex-regenten of the old Dutch Republic and advised them to end their staying out of government. That meant that some of his instructions given in the Kew Letters, which urged resistance against the French–Batavian invasion, were no longer in effect. He and his son, William Freder...

Village in Massachusetts, United States The Second Church of Plymouth at Manomet Manomet is a seaside village of Plymouth, Massachusetts, United States. It is named for the Wampanoag village of Manomet, located among the Manomet Ponds (the later site of the Manomet Ponds Praying Town).[1] Manomet has a Post Office in the business district whose ZIP code is 02345. Residents and businesses in this village that are non-Post Office box holders use Plymouth's ZIP code of 02360. Manomet is ...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Harris Effendi Thahar BiografiKelahiran4 Januari 1950 (74 tahun)Tembilahan Data pribadiKelompok etnikOrang Minangkabau PendidikanUniversitas Negeri Padang Universitas Negeri Jakarta KegiatanPekerjaanpenulis Bekerja diUniversitas Negeri Padang KeluargaAnakIsa Gautama Prof. Dr. Harris Effendi Thahar, M.Pd. (lahir 4 Januari 1950) adalah seorang guru besar Universitas Negeri Padang, akademisi, dan sastrawan berkebangsaan Indonesia yang banyak menulis cerita pendek (cerpen) dan sajak. Namanya terc...

Acetil-CoA Nombre IUPAC [(2R,3S,4R,5R)-2-[([((3R)-4-([3-(2acetilsulfaniletilamino)-3-oxopropil]amino)-3-hidroxi-2,2-dimetil-4-oxobutoxi]-oxidofosforil)oxi-oxidofosforil]oximetil)-5-(6-aminopurin-9-il)-4-hidroxioxolan-3-il] fosfatoGeneralOtros nombres S-Acetil coenzima AFórmula estructural Fórmula molecular C23H38N7O17P3SIdentificadoresNúmero CAS 72-89-9[1]ChEBI 15351ChemSpider 392413PubChem 444493UNII 76Q83YLO3OKEGG C00024 InChIInChI=InChI=1S/C23H38N7O17P3S/c1-12(31)51-7-6...

Pour les articles homonymes, voir Iulius Caesar. Sextus Julius CaesarPièce de monnaie frappée par Sextus Julius Caesar.FonctionsSénateur romainjusqu'en 90 av. J.-C.Consulavec Lucius Marcius Philippus91 av. J.-C.Préteuravant 93 av. J.-C.BiographieNaissance Rome antiqueDécès 90 av. J.-C.Ascoli Piceno (Rome antique)Nom dans la langue maternelle Sex. Iulius C.f. CaesarÉpoque République romaine tardive (en)Activités Homme politique de la Rome antique, militaire romainFamille Julii Caesar...

President of the Maldives from 2013 to 2018 The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (May 2019) (Learn how and when to remove this message) Abdulla Yameen Abdul Gayoomޢަބްދުﷲ ޔާމީން ޢަބްދުލް ޤައްޔޫމްOfficial portrait, 20156th President of the MaldivesIn office17 November 2013 – 17 November 2018Vice President Mohamed Jameel Ahmed(20...

فسيفساء رومانية في جرش بالأردن للشاعرة اليونانية الكمان تظهر شرب الخمر. أواخر القرن الثاني والثالث معصرة نبيذ أثرية في عبدون يتم إنتاج النبيذ الأردني من قبل اثنين من مصانع النبيذ، مع إنتاج سنوي ما يقرب من مليون زجاجة في السنة. للأردن تقليد طويل في صناعة النبيذ، [1] يعود...

The Open University (OU) UbicazioneStato Regno Unito CittàMilton Keynes Dati generaliMotto'Learn and Live' Fondazione1969 FondatoreHarold Wilson Tipouniversità statale RettoreBaronessa Lane-Fox of Soho Studenti168 215 Dipendenti11 472 AffiliazioniUniversity Alliance Mappa di localizzazione Sito web e Sito web Modifica dati su Wikidata · Manuale La Open University (OU) è un'università pubblica di ricerca specializzata nell'insegnamento a distanza, e una delle più gran...

This article may need to be rewritten to comply with Wikipedia's quality standards, as there are too many country infoboxes, two of which overlap dates. You can help. The talk page may contain suggestions. (November 2023) Part of a series on the History of Chad Kanem–Bornu Empire Sultanate of Bagirmi Wadai Sultanate French colonial period Tombalbaye government Civil War (1965–1979) Malloum government Transitional Government Habré Era Conflict with Libya Toyota War Déby era Civil War (2...

2011 film by Ben Palmer The Inbetweeners MovieTheatrical release posterDirected byBen PalmerWritten byDamon BeesleyIain MorrisBased onThe Inbetweenersby Damon Beesley and Iain MorrisProduced byChristopher YoungStarringSimon BirdJames BuckleyBlake HarrisonJoe ThomasCinematographyBen WheelerEdited byWilliam WebbCharlie FawcettMusic byMike SkinnerProductioncompaniesFilm4 ProductionsBwark ProductionsYoung FilmsDistributed byEntertainment Film Distributors (United Kingdom)IM Global (International)...
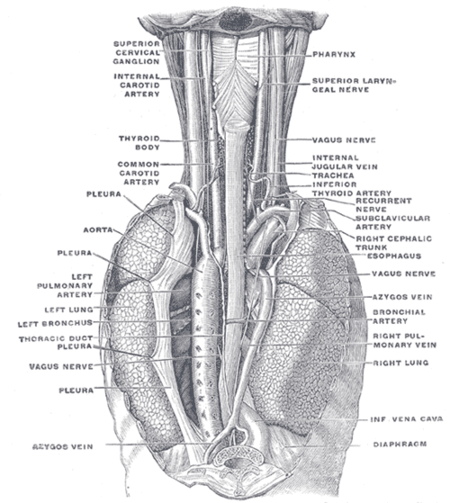
Blood vessels supplying the lungs Bronchial arteryBronchial artery labeled at center rightDetailsSourceThoracic aortaVeinBronchial veinsSuppliesLungsIdentifiersLatinarteriae bronchiales, rami bronchiales partis thoracicae aortaeMeSHD001981TA98A12.2.11.002TA24579FMA68109 71536, 68109Anatomical terminology[edit on Wikidata] In human anatomy, the bronchial arteries supply the lungs with oxygenated blood, and nutrition. Although there is much variation, there are usually two bronchial arterie...

Disambiguazione – Keplero rimanda qui. Se stai cercando altri significati, vedi Keplero (disambigua). Giovanni Keplero nel 1620 Giovanni Keplero, adattamento di Johannes Kepler[1][2][3][4] (Weil der Stadt, 27 dicembre 1571 – Ratisbona, 15 novembre 1630), è stato un astronomo, astrologo, matematico, cosmologo, filosofo della natura e teologo luterano tedesco, che scoprì le leggi omonime che regolano i movimenti dei pianeti. Matematico imperiale da...

























