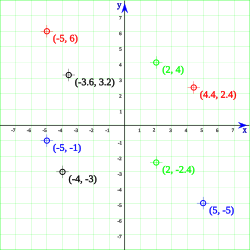
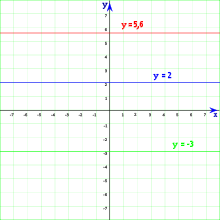
Xeometría analítica
|
Read other articles:
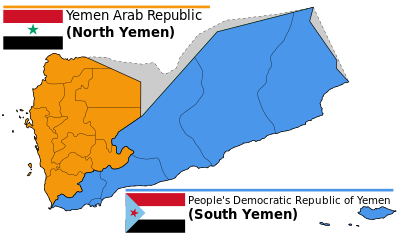
Penyatuan Yaman atau Unifikasi Yaman terjadi pada 22 Mei 1990, saat kawasan Republik Demokratik Rakyat Yaman (juga dikenal sebagai Yaman Selatan) bersatu dengan Republik Arab Yaman (juga dikenal sebagai Yaman Utara), membentuk Republik Yaman (disingkat Yaman). Latar belakang Yaman Utara (jingga) dan Yaman Selatan (biru) sebelum 1990. Tidak seperti Jerman Timur dan Jerman Barat, Tiongkok Komunis dan Nasionalis, Korea Utara dan Korea Selatan, atau Vietnam Utara dan Vietnam Selatan, dua Yaman ta...

Estonian football club This article is about the men's football club. For the women's team, see Tartu JK Tammeka (women). Football clubTammekaFull nameTartu Jalgpallikool TammekaFounded13 June 1989; 34 years ago (1989-06-13)GroundTartu Tamme StadiumCapacity1,750[1]ChairmanKristjan TiirikManagerMarti PähnLeagueMeistriliiga2023Meistriliiga, 9th of 10WebsiteClub website Home colours Away colours Tartu JK Tammeka, commonly known as Tartu Tammeka or simply Tammeka, is an...

Cet article concerne la voiture de la marque Pontiac. Pour le championnat automobile Trans-Am, voir Trans-Am Series. Pontiac Firebird Marque Pontiac Années de production 1967 - 2002 Classe Pony car / Muscle car modifier La Pontiac Firebird est un coupé sportif produit entre 1967 et 2002 en quatre générations distinctes. On peut facilement la confondre avec sa jumelle, la Chevrolet Camaro dont la Firebird est directement issue. Leur châssis est de type « F-Body » et...

Far-right anti-semitic conspiracy theory Richard von Coudenhove-Kalergi, supposed creator of the plan, pictured c. 1930 The Kalergi Plan, sometimes called the Coudenhove-Kalergi Conspiracy,[1] is a debunked far-right, antisemitic, white genocide conspiracy theory.[2][3] The theory claims that Austrian-Japanese politician Richard von Coudenhove-Kalergi, creator of the Paneuropean Union, concocted a plot to mix and replace white Europeans with other races via immigration...

Richard Baxter Richard Baxter (Rowton, 12 novembre 1615 – Londra, 8 dicembre 1691) è stato un religioso britannico. Predicatore puritano molto celebre sotto il regno di Carlo I d'Inghilterra; raggiunse ulteriore notorietà con l'autobiografia Reliquiae Baxterianae, che conteneva tra l'altro note di interesse storiografico. Dopo vari anni di ministero la sua reputazione di ministro si affermò a Kidderminster, dove cominciò una lunga e prolifica produzione di scritti teologici. Dopo la Res...

Brian France CEO dan ketua NASCARMasa jabatanSeptember 2003 – 5 Agustus 2018PendahuluBill France Jr.PenggantiJim France Informasi pribadiLahirBrian Zachary FranceAugust 2, 1962 (1962-08-02) (usia 61)Daytona Beach, FloridaSuami/istriAmy FranceAnak4Orang tuaBill France Jr. (ayah)KerabatBill France Sr. (kakek)Jim France (paman)Lesa Kennedy (saudara kandung)Alma materUniversity of Central FloridaSunting kotak info • L • B Brian France (lahir 2 Agustus 1962) merupakan...

South Africa dual-code international rugby player Rugby playerGary BothaFull nameGary van Ginkel BothaDate of birth (1981-10-12) 12 October 1981 (age 42)Place of birthPretoria, South AfricaHeight1.80 m (5 ft 11 in)Weight106 kg (16 st 10 lb; 234 lb)Rugby league careerInternational careerYears Team Apps (Points)2000 South Africa ()Rugby union careerPosition(s) HookerSenior careerYears Team Apps (Points)2002–2006 Blue Bulls ()2003 Sharks 10 (5)2004–200...

French footballer and manager (born 1954) René Girard Girard in 2012Personal informationDate of birth (1954-04-04) 4 April 1954 (age 70)[1]Place of birth Vauvert, FranceHeight 1.78 m (5 ft 10 in)[2]Position(s) Defensive midfielderSenior career*Years Team Apps (Gls)1973–1980 Nîmes 202 (27)1980–1988 Bordeaux 241 (17)1988–1991 Nîmes 92 (5)Total 535 (49)International career1981–1982 France 7 (1)Managerial career1991–1994 Nîmes1996–1997 Pau FC199...

У этого термина существуют и другие значения, см. Чайки (значения). Чайки Доминиканская чайкаЗападная чайкаКалифорнийская чайкаМорская чайка Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:Вторич...

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Setono, Jenangan, Ponorogo – berita · surat kabar · buku · cendekiawan · JSTOR SetonoKelurahanNegara IndonesiaProvinsiJawa TimurKabupatenPonorogoKecamatanJenanganKode Kemendagri35.02.18.1001 Kode BP...

طبق كراهي اللحم المطبخ الباكستاني (بالأردية: پاکستانی پکوان) هو مطبخ عريق وراق من مزيج من المأكولات المختلفة المعروفة باكستان. ومن المعروف عن المطبخ الباكستاني ثرائه ونكهته الغنية.[1] تختلف الاطباق داخل باكستان اختلافا كبيرا من منطقة إلى أخرى، والتي تعكس التنوع العرقي ...

Prehistoric lake in New Mexico, United States Lake EstanciaLake EstanciaLocation of Lake Estancia in New MexicoA map of the position of the former shorelines of Lake EstanciaLocationEstancia Valley, New MexicoCoordinates35°N 106°W / 35°N 106°W / 35; -106Typeformer lakeMax. length56 kilometres (35 miles)Max. width37 kilometres (23 miles) Lake Estancia was a lake formed in the Estancia Valley, central New Mexico, which left various coastal landforms in the valley. Th...

Colonists loyal to the British Crown during the American Revolution For other uses, see Loyalism and Loyalist (disambiguation). Britannia offers solace and a promise of compensation for her exiled American-born British Loyalists. (Reception of the American Loyalists by Great Britain in the Year 1783, engraving by Henry Moses after a painting by Benjamin West.) Flag of the United Empire Loyalists. Loyalists were colonists in the Thirteen Colonies who remained loyal to the British Crown during ...

乔冠华 中华人民共和国外交部部长 中国人民对外友好协会顾问 任期1974年11月—1976年12月总理周恩来 → 华国锋前任姬鹏飞继任黄华 个人资料性别男出生(1913-03-28)1913年3月28日 中華民國江蘇省盐城县逝世1983年9月22日(1983歲—09—22)(70歲) 中华人民共和国北京市籍贯江蘇鹽城国籍 中华人民共和国政党 中国共产党配偶明仁(1940年病逝) 龚澎(1970年病逝) 章含�...

Football match2019 Supercoppa ItalianaEventSupercoppa Italiana Juventus Lazio Serie A Coppa Italia 1 3 Date22 December 2019VenueKing Saud University Stadium, Riyadh, Saudi Arabia[1]RefereeGianpaolo CalvareseAttendance23,361← 2018 2020 → The 2019 Supercoppa Italiana (branded as the Coca-Cola Supercup for sponsorship reasons)[2] was the 32nd edition of the Supercoppa Italiana, the Italian football super cup. It was played on 22 December 2019 by defending champions Ju...

ناصر محمد القحطاني معلومات شخصية الميلاد 1970 (العمر 54 سنة)بلدة صبحا الإقامة الرياض مواطنة السعودية الجنسية سعودي اللقب شاعر الأندلس الديانة مسلم الحياة العملية التعلّم بكالوريوس بحوث العمليات من جامعة الملك سعود بالرياض المهنة شاعر وإعلامي المواقع الموقع https://nkahtani.com تعد�...

Qatari footballer Mohamed El-Sayed Jeddo playing for Qatar in 2011Personal informationFull name Mohamed El-Sayed AbdulmotalebDate of birth (1987-01-27) 27 January 1987 (age 37)Place of birth Dukhan, QatarHeight 1.83 m (6 ft 0 in)Position(s) WingerTeam informationCurrent team Al-ShamalNumber 34Senior career*Years Team Apps (Gls)2007–2012 Umm-Salal 82 (4)2012–2016 El Jaish 53 (2)2014–2015 → Umm-Salal (loan) 22 (2)2016–2019 Umm-Salal 33 (3)2019–2021 Al-Khor 24 (0)...

1971 film by James Goldstone Red Sky at MorningDirected byJames GoldstoneWritten byRichard Bradford (story)Marguerite RobertsProduced byHal B. WallisStarringRichard ThomasCatherine BurnsDesi Arnaz, Jr.Richard CrennaClaire BloomHarry GuardinoCinematographyVilmos ZsigmondEdited byEdward A. BieryRichard M. SpragueMusic byBilly GoldenbergThe Andrews SistersProductioncompanyHal Wallis Productions[1]Distributed byUniversal PicturesRelease date May 12, 1971 (1971-05-12) Runnin...

French businessman, historian and diplomat François Charles-Roux (19 November 1879 – 26 June 1961)[1] was a French businessman, historian and diplomat. He was born in Marseille. Biography Charles-Roux, the son of Jules Charles-Roux, studied at the École libre des sciences politiques. This led to a diplomatic career in Paris, St. Petersburg, Constantinople, Cairo, London and Prague before being appointed Ambassador of France to the Holy See in 1932. In May 1940, he succeeded Alexis...