Théorie ergodique
|
Read other articles:

Maltodekstrin Penanda Nomor CAS 9050-36-6 Y 3DMet {{{3DMet}}} ChemSpider NA N Nomor EC PubChem CID 62698 Nomor RTECS {{{value}}} UNII 7CVR7L4A2D Y CompTox Dashboard (EPA) DTXSID5027720 Sifat Rumus kimia C6nH(10n+2)O(5n+1) Massa molar bervariasi Penampilan serbuk putih Titik lebur 240 °C Kelarutan dalam air Mudah larut atau mudah terdispersi dalam air[1] Kelarutan sedikit larut hingga tidak larut dalam alkohol anhidrat[1] Bah...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (August 2020) (Learn how and when to remove this template message) This article may contain citations that do not verify the text. Please check for citation inaccuracies. (August ...

Performing the service in the armed forces of a state For recruitment for military employment, see Military recruitment. For state-mandated military service, see Conscription. For the feudal institution, see Knight-service. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to relia...

Bridge in Ontario, CanadaRosedale Valley BridgeCoordinates43°40′21″N 79°22′15″W / 43.67263°N 79.37071°W / 43.67263; -79.37071CarriesLine 2 Bloor–DanforthCrossesRosedale Ravine Rosedale Valley RoadLocaleToronto, Ontario, CanadaOther name(s)Rosedale Ravine BridgeMaintained byToronto Transit CommissionCharacteristicsDesignCovered arch bridgeMaterialSteel and concreteNo. of spans1HistoryConstructed byJohn B. ParkinConstruction start1965Construction end1966Ope...
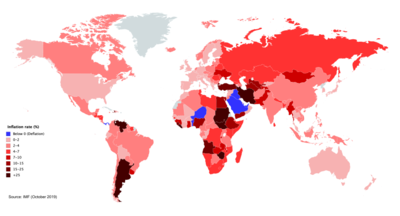
Disambiguazione – Se stai cercando la teoria cosmologica, vedi Inflazione (cosmologia). Fonte: OECD Data. Tasso di inflazione nei diversi paesi nel 2019 Con inflazione (dal latino inflatio «enfiamento, gonfiatura», derivato da inflāre «gonfiare»[1]), in economia, si indica l'aumento prolungato del livello medio generale dei prezzi di beni e servizi in un determinato periodo di tempo, che genera una diminuzione del potere d'acquisto della moneta.[2][3] L'inflazi...

Untuk candi di Bali, lihat Candi Gunung Kawi. Gunung KawiRangkaian Pegunungan Butak-Kawi-Panderman. Gunung Kawi terletak kedua dari kanan.Titik tertinggiKetinggian2,551 m (8,369 kaki)[1]Koordinat7°55′S 112°27′E / 7.92°S 112.45°E / -7.92; 112.45 GeografiLetakJawa Timur, IndonesiaGeologiUsia batuanHoloceneJenis gunungStratovolcano Gunung Kawi adalah sebuah gunung berapi yang sudah lama tidak aktif, berada sebelah barat daya di Kabupaten Ma...

Intersex rights in ArgentinaArgentinaProtection of physical integrity and bodily autonomyNoProtection from discriminationNoAccess to identification documentsNoChanging M/F sex classificationsYesThird gender or sex classificationsYesMarriageYes Rights by country Argentina Australia Canada Chile China Colombia France Germany Kenya Malta Mexico Nepal New Zealand South Africa Spain Switzerland Taiwan Uganda United Kingdom United States Intersex topics Human rights and legal issues Compulsory ster...

Study of international math and science skills This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this message) TIMSS 8th grade average Mathematics scores (2...

IIe législature de la Cinquième République française 6 décembre 1962 - 2 avril 19674 ans, 3 mois et 27 jours Assemblée nationale Composition UNR-UDT (233) SOC (66) CD (55) COM (41) RD (39) RI (35) Non inscrits (13) Président Jacques Chaban-Delmas (UNR)9 décembre 1958-20 juin 1969 Élections 18 et 25 novembre 1962 Sénat Président Gaston Monnerville (RAD)9 décembre 1958-3 octobre 1968 Élections Gouvernement Parti(s) UNR-UDT, UDVe, UDR - RI, FNRI Gouvernement(s) Pompi...

le Nouzet Caractéristiques Longueur 15,5 km Bassin collecteur Loire Régime pluvial Cours Source la Brande de Rossine · Localisation Saint-Hilaire-en-Lignières · Altitude 189 m · Coordonnées 46° 46′ 22″ N, 2° 08′ 28″ E Confluence l'Arnon · Localisation Mareuil-sur-Arnon · Altitude 135 m · Coordonnées 46° 52′ 35″ N, 2° 08′ 06″ E Géographie Pays traversés France Département Cher Régions...

Флаг гордости бисексуалов Бисексуальность Сексуальные ориентации Бисексуальность Пансексуальность Полисексуальность Моносексуальность Сексуальные идентичности Би-любопытство Гетерогибкость и гомогибкость Сексуальная текучесть Исследования Шк...

Historic district in California, United States United States historic placePasadena Civic Center DistrictU.S. National Register of Historic PlacesU.S. Historic district Pasadena City Hall, 2008LocationPasadena, CaliforniaArchitectural styleBeaux ArtsNRHP reference No.80000813[1]Added to NRHPJuly 28, 1980 The Pasadena Civic Center District is the civic center of and a historic district in Pasadena, California, United States. The district is roughly bounded by Walnut and ...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Persenga Nganjuk – berita · surat kabar · buku · cendekiawan · JSTOR Persenga NganjukNama lengkapPersatuan Sepak Bola NganjukJulukanLaskar Singo Barong(The Lassib)Berdiri17 Agustus 1950StadionStadion Anj...

Пам'ятник Анатолію Солов'яненку Країна Україна Адміністративна одиниця Донецьк Місце розташування Theatre Squared Жанр публічне мистецтво На честь Солов'яненко Анатолій Борисович Статус спадщини пам'ятка монументального мистецтва України місцевого значенняd Описан�...

2017 film by Nicolas Bedos Mr. & Mrs. AdelmanTheatrical release posterFrenchMonsieur & Madame Adelman Directed byNicolas BedosScreenplay by Nicolas Bedos Doria Tillier Dialogue byNicolas Bedos Produced by François Kraus Denis Pineau-Valencienne Starring Doria Tillier Nicolas Bedos Denis Podalydès Antoine Gouy Christiane Millet Pierre Arditi Zabou Breitman Julien Boisselier CinematographyNicolas BolducEdited by Anny Danché Marie Silvi Music by Philippe Kelly Nicolas Bedos Production...

English musician; bassist for The Who (1944–2002) For the English cyclist, see John Entwistle (cyclist). For the English Member of Parliament, see John Entwistle (politician). John EntwistleEntwistle at Maple Leaf Gardens in Toronto, Canada, 1976Background informationBirth nameJohn Alec EntwistleAlso known asThe OxThunderfingersThe Quiet OneBig Johnny TwinkleBorn(1944-10-09)9 October 1944Chiswick, Middlesex, EnglandDied27 June 2002(2002-06-27) (aged 57)Paradise, Nevada, U.S.GenresRockh...

此條目需要补充更多来源。 (2019年9月13日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:台中馬禮遜美國學校 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 馬禮遜學校Morrison Academy馬禮遜學校Morrison Academy地址 中華民國臺�...

Tlatoani of Tlatelolco QuauhtlatoaKing QuauhtlatoaTlatoani of TlatelolcoPredecessorTlacateotlSuccessorMoquihuixFatherPrince Acolmiztli of Tlatelolco Quauhtlatoa (or Cuauhtlatoa) (1 Flint (1428)[1] – 4 Reed (1431)[2]/7 Flint (1460)[3]/8 House (1461)[4]) was a tlatoani (king, ruler) of the Nahua city-state Tlatelolco. Biography He was a son of Prince Acolmiztli of Tlatelolco, grandson of the King Tlacateotl and great-grandson of Quaquapitzahuac. He was a succes...

لمعانٍ أخرى، طالع باتلر (توضيح). باتلر الإحداثيات 43°10′52″N 76°46′23″W / 43.181111111111°N 76.773055555556°W / 43.181111111111; -76.773055555556 [1] تاريخ التأسيس 1803 تقسيم إداري البلد الولايات المتحدة التقسيم الأعلى مقاطعة وين خصائص جغرافية المساحة 37.17 ميل مربع&...







































