K-théorie
|
Read other articles:

Arjun KapoorKapoor di sebuah acara promosional untuk film MubarakanLahir26 Juni 1985 (umur 38)[1]Mumbai, Maharashtra, IndiaPekerjaanPemeranTahun aktif2012–sekarangOrang tuaBoney Kapoor (ayah) Mona Shourie Kapoor (ibu)KerabatLihat Keluarga Kapoor Arjun Kapoor (pelafalan [ɐrˈɟun kəˈpuːr]; lahir 26 Juni 1985) adalah seorang pemeran India yang tampil dalam perfilman Bollywood. Ia adalah putra dari produser film Boney Kapoor dan Mona Shourie Kapoor. Setelah berka...

Motion problem in classical mechanics This article is about the two-body problem in classical mechanics. For the relativistic version, see Two-body problem in general relativity. For the career management problem of working couples, see Two-body problem (career). Left: Two bodies with similar mass orbiting a common barycenter external to both bodies, with elliptic orbits—typical of binary stars . Right: Two bodies with a slight difference in mass orbiting a common barycenter. The sizes, and...

Pancuran Malaikat Jatuh karya Ricardo Bellver, 1877, Taman Retiro (Madrid, Spanyol) Malaikat-Malaikat Jatuh (1893) karya Salvatore Albano di Museum Brooklyn Kota New York Malaikat jatuh dalam istilah agama Abrahamik adalah malaikat yang terusir dari surga. Istilah literal malaikat jatuh tidak terdapat kitab suci agama-agama Abrahamik mana pun, tetapi digunakan untuk menggambarkan malaikat-malaikat yang tersingkir dari surga[1] atau malaikat-malaikat berdosa. Malaikat-malaikat semacam ...

Antonio Giolitti Commissario europeo per la politica regionaleDurata mandato6 gennaio 1977 –5 gennaio 1985 PresidenteRoy JenkinsGaston Thorn PredecessoreGeorge Thomson SuccessoreGrigoris Varfis Ministro del bilancioDurata mandato5 dicembre 1963 –23 luglio 1964 Capo del governoAldo Moro PredecessoreGiuseppe Medici SuccessoreGiovanni Pieraccini Ministro del bilancio e della programmazione economicaDurata mandato28 marzo 1970 –18 febbraio 1972 Capo...

2012 Harlow District Council election ← 2011 3 May 2012 2014 → 11 of the 33 seats to Harlow District Council17 seats needed for a majority First party Second party Third party Party Labour Conservative Liberal Democrats Seats before 14 17 2 Seats won 7 4 0 Seats after 20 13 0 Seat change 6 4 2 Popular vote 9,722 7,083 1,467 Percentage 52.1% 38.0% 7.9% Map showing the results of contested wards in the 2012 Harlow District Council el...

American independent professional wrestling promotion SukebanFoundedSeptember 1, 2023; 8 months ago (2023-09-01)StyleProfessional wrestlingJoshi PuroresuHeadquartersNew York CityOwner(s)Dream Slam ProductionsWebsitesukeban.com Sukeban is an American independent women's professional wrestling promotion. In Japanese culture, Sukeban is an ode to the girl gangs in the 60's and 70's, which the promotion is influenced by as the roster is consisted by different units.[1]&...

إميل أرتين (بالألمانية: Emil Artin) معلومات شخصية الميلاد 3 مارس 1898(1898-03-03)فيينا، النمسا الوفاة 20 ديسمبر 1962 (64 سنة)هامبورغ، ألمانيا مواطنة الإمبراطورية النمساوية المجرية الولايات المتحدة النمسا عضو في الأكاديمية الألمانية للعلوم - ليوبولدينا، والأكاديمية الأمريكية ...

مبادرة مستقبل الاستثمارشعار مبادرة مستقبل الاستثمارمعلومات عامةالحالة مستمرالنوع اقتصادتاريخ البداية منتصف شهر أكتوبرتاريخ الانتهاء منتصف شهر أكتوبرالتكرر سنويًاالمبنى ريتز كارلتونالمكان الرياضالبلد السعوديةسنوات النشاط 2017-الانتاريخ التأسيس 24 أكتوبر 2017المؤسس ا...

Indian actor For other people named Ram Charan, see Ram Charan (disambiguation). Ram CharanRam Charan in 2022BornKonidela Ram Charan[1] (1985-03-27) 27 March 1985 (age 39)Madras, Tamil Nadu, IndiaAlma materSt. Mary's College, HyderabadOccupationsActorfilm producerentrepreneurYears active2007–presentSpouse Upasana Kamineni (m. 2012)Children1ParentChiranjeevi (father)RelativesPawan Kalyan (uncle) Shobana Kamineni (mother-in-law) Allu Arjun...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Members of the New South Wales Legislative Assembly who served in the 29th parliament held their seats from 1930 to 1932. They were elected at the 1930 state election,[1] and at by-elections.[2][3][4] The Nationalist Party was replaced by the United Australia Party in 1931. The Speaker was Frank Burke.[5] Name Party Electorate Term in office George Ardill Nationalist Yass 1930–1941 Richard Arthur Nationalist Mosman 1904–1932 Jack Badd...

Administrative division of Uttar Pradesh, India Gorakhpur division Gorakhpur division is one of the 18 administrative geographical units (i.e. division) of the northern Indian state of Uttar Pradesh. Gorakhpur city is the administrative headquarters of the division. The division consists of 4 districts.[1] PlaceCommissionery OfficeGovernment • Divisional CommissionerJayant Narlikar[2][3] Districts Gorakhpur Deoria Kushinagar Maharajganj History In the year ...

Shan XiaonaInformasi pribadiKewarganegaraanJermanLahir18 Januari 1983 (umur 41)Anshan, Liaoning, ChinaTinggi165 m (541 ft 4 in)Berat54 kg (119 pon) OlahragaNegara GermanyOlahragatenis meja Rekam medali Olimpiade 2016 Rio de Janeiro Team Pesta Olahraga Eropa 2015 Baku Team 2019 Minsk Team Shan Xiaona (Hanzi sederhana: 单晓娜; Hanzi tradisional: 單曉娜; lahir 18 Januari 1983)[1] adalah pemain tenis meja Jerman. Dia mewakili negaranya di O...

SDN 03 BotumoitoSekolah Dasar Negeri 03 BotumoitoInformasiJenisSekolah DasarNomor Pokok Sekolah Nasional40500133Kepala SekolahRatna MusaModeratorSri Dewi AdipuJumlah kelas7Rentang kelasI-VIKurikulumkurikulum 2013StatusNegeriAlamatLokasiJln. Trans Sulawesi, Desa Tutulo, Boalemo, Gorontalo, IndonesiaTel./Faks.085298522421Koordinat0°29′51″N 123°17′53″E / 0.4975483°N 123.2980000°E / 0.4975483; [email protected] SD Negeri 03 ...

Ethnolinguistic and geographical region in South Asia This article is about the geographical region. For the province of Pakistan, see Punjab, Pakistan. For the state in India, see Punjab, India. For other uses, see Punjab (disambiguation). RegionPunjab PanjābRegionNickname: Land of the Five RiversLocation of Punjab in South AsiaCoordinates: 31°N 74°E / 31°N 74°E / 31; 74Countries Pakistan IndiaLargest cityLahoreSecond Largest cityFaisalabadNamed fo...

Bungli Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Asterid Ordo: Lamiales Famili: Bignoniaceae Tribus: Oroxyleae Genus: OroxylumVent. Spesies: Oroxylum indicum(L.) Benth. ex Kurz Sinonim[2] Arthrophyllum ceylanicum Miq. Arthrophyllum reticulatum Blume ex Miq. Bignonia indica L. Bignonia lugubris Salisb. Bignonia pentandra Lour. Bignonia quadripinnata Blanco Bignonia tripinna...
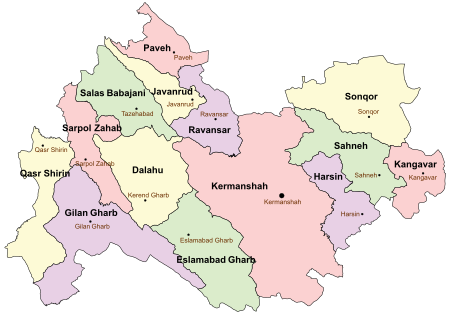
Province of Iran Not to be confused with Kermanshah County.For the city, see Kermanshah. Province in 4th Region, IranKermanshah Province Persian: استان کرمانشاهProvinceLocation of Kermanshah Province within IranCoordinates: 34°33′N 46°43′E / 34.550°N 46.717°E / 34.550; 46.717[1]CountryIranRegion4th RegionCapitalKermanshahCounties14Government • Governor-generalMohammad-Tayyeb Sahraee • MPs of Assembly of ExpertsAman N...

Former local government area in New South Wales, Australia Bingara ShireNew South WalesLocation within New South WalesPopulation2,029 (2004)[1] • Density0.71101/km2 (1.8415/sq mi)Established1 January 1944 (1944-01-01)Abolished17 March 2004 (2004-03-17)Area2,853.7 km2 (1,101.8 sq mi)Council seatBingaraRegionNew England LGAs around Bingara Shire: Moree Plains Yallaroi Inverell Moree Plains Bingara Shire Guyra Narrabri Barraba...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2023) هيديو إيشيكاوا (باليابانية: 石川英郎) معلومات شخصية الميلاد 13 ديسمبر 1969 (العمر 54 سنة)نيشينومايا، هيو�...

Bài viết này trong loại bàiKinh tế học Các nền kinh tế theo vùng Châu Phi · Bắc Mỹ Nam Mỹ · Châu Á Châu Âu · Châu Đại Dương Đề cương các chủ đề Phân loại tổng quát Kinh tế học vi mô · Kinh tế học vĩ mô Lịch sử tư tưởng kinh tế Lý luận · Các phương pháp không chính thống Các phương pháp kỹ thuật Toán học &...























