Número de Betti
|
Read other articles:

1999 compilation album by CatatoniaThe Crai-EPs 1993/1994Compilation album by CatatoniaReleased19 October 1999GenrePop, rockLength26.27LabelCraiCatatonia chronology Equally Cursed and Blessed(1999) The Crai-EPs 1993/1994(1999) Paper Scissors Stone(2001) Professional ratingsReview scoresSourceRatingAllmusic[1]NME(7/10)[2] The Crai-EPs 1993/1994 is a compilation of two EPs released by the band Catatonia; For Tinkerbell (the first five tracks) and Hooked (the last three t...

Monthly magazine (1902–1953 The SphinxThe cover of the first issueFrequencyMonthlyFounderWilliam J. HilliarFirst issueMarch 1902 (1902-03)Final issueNumberMarch 1953 (1953-03)597 The Sphinx (subtitled: An Independent Magazine for Magicians) was a monthly magic magazine published in Chicago from March 1902 through March 1953 by William J. Hilliar.[1] History and profile The magazine was started in Chicago by William Hilliar and moved to Missouri in 1904 when a Kan...

Ini adalah nama Jepang, nama keluarganya adalah Shirakawa. Yoshinori ShirakawaLahir24 Januari 1869Iyo, JepangMeninggal26 Mei 1932(1932-05-26) (umur 63)Shanghai, TiongkokPengabdian JepangDinas/cabang Angkatan Darat Kekaisaran JepangLama dinas1890–1932PangkatJenderalKomandan Divisi Infanteri ke-11 Divisi Infanteri ke-1 Tentara Kwantung Tentara Ekspedisi Shanghai Perang/pertempuran Perang Tiongkok-Jepang Pertama Perang Rusia-Jepang Perang Dunia I Penghargaan Ordo Layang Ema...
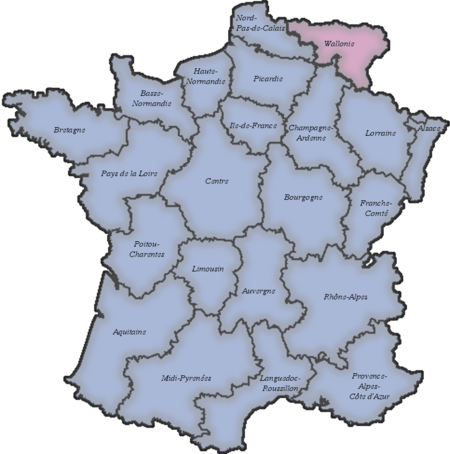
Bendera pergerakan rattachisme Peta region Prancis (sebelum reformasi tahun 2014) ditambah dengan Wallonia Rattachisme (Prancis: Rattachismecode: fr is deprecated , IPA: [ʁataʃism], reattach-ism) atau Reunionisme (Réunionisme) adalah ideologi politik yang menyerukan agar wilayah berbahasa Prancis di Belgia atau Wallonia memisahkan diri dari negara Belgia dan bergabung dengan Prancis. Brussel (yang terletak di tengah-tengah Flandria tetapi kebanyakan penduduknya saat ini berbahasa Pran...

Artikel ini bukan mengenai arXiv. Koordinat: 37°46′56.3″N 122°28′17.65″W / 37.782306°N 122.4715694°W / 37.782306; -122.4715694 Internet Archive Motouniversal access to all knowledge DataNama singkatIA Tipearsip Perpustakaan digital organisasi nirlaba situs web arsip Internet SpesialisasiPengarsipan web dan Pelestarian digital Bentuk legal501(c)(3) organization (en) SejakMei 1996PendiriBrewster Kahle KegiatanMemproduksiCover Art Archive (en) Anggota dariAmer...

Меркенский районМеркі ауданы Герб 42°53′ с. ш. 73°11′ в. д.HGЯO Страна Казахстан Входит в Жамбылскую область Включает 14 сельских округов Адм. центр село Мерке Аким района Жорабек Баубеков[1] История и география Дата образования 27 декабря 1933 года Площадь 7,1 тыс...

2011 studio album by Jessie JWho You AreStudio album by Jessie JReleased25 February 2011 (2011-02-25)Recorded2005 – 19 January 2011StudioScala, London, UK, and studios: Conway, Hollywood, California, US; GCR Audio, Buffalo, New York, US; Grove, London; Herminator, London; Quad, New York City; RAK, London; Santisound, Los Angeles, California; Stadium Red, New York City; Strawberry Bee, Hollywood Hills, CaliforniaGenrePop[1]Length50:14Label Lava Island Universa...

UnstoppableSingel oleh Siadari album This Is ActingDirilis2022Direkam2015GenreElectropopDurasi3:37LabelMonkey PuzzleRCAPencipta Sia Furler Christopher Braide ProduserJesse ShatkinKronologi singel Sia Dynamite (2022) Unstoppable (2022) Gimme Love (2023) Live videoUnstoppable (Live from the Nostalgic For The Present Tour) di YouTube Unstoppable adalah lagu oleh penyanyi-penulis lagu asal Australia, Sia, diambil dari album studio ketujuhnya, This Is Acting (2016). Lagu ini ditulis oleh Sia dan C...

Australian cricketer For the squash player, see Cameron White (squash player). Cameron WhitePersonal informationFull nameCameron Leon WhiteBorn (1983-08-18) 18 August 1983 (age 40)[1]Bairnsdale, Victoria, AustraliaNicknameWhitey, Bear, BundyHeight1.87[2] m (6 ft 2 in)BattingRight-handedBowlingRight-arm leg breakInternational information National sideAustralia (2005-2018)Test debut (cap 402)9 October 2008 v IndiaLast Test6 November 20...

American politician Aaron ShawMember of the U.S. House of Representativesfrom Illinois's 16th districtIn officeMarch 4, 1883 – March 3, 1885Preceded byJames C. AllenSucceeded byJames C. RobinsonMember of the U.S. House of Representativesfrom Illinois's 7th districtIn officeMarch 4, 1857 – March 3, 1859Preceded byWilliam A. J. SparksSucceeded bySilas Z. LandesMember of the Illinois House of RepresentativesIn office1850 Personal detailsBorn(1811-12-19)December 19, 18...

Spanish footballer In this Spanish name, the first or paternal surname is Palencia and the second or maternal family name is Hurtado. Sergi Palencia Palencia in 2012Personal informationFull name Sergi Palencia HurtadoDate of birth (1996-03-23) 23 March 1996 (age 28)Place of birth Badalona, SpainHeight 1.68 m (5 ft 6 in)[1]Position(s) Right-backTeam informationCurrent team Los Angeles FCNumber 14Youth career2004–2006 Badalona2006–2015 BarcelonaSenior car...

Japanese television series The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Ultraman Blazar – news · newspapers · books · scholar&...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

国民阵线Barisan NasionalNational Frontباريسن ناسيونلபாரிசான் நேசனல்国民阵线标志简称国阵,BN主席阿末扎希总秘书赞比里署理主席莫哈末哈山总财政希山慕丁副主席魏家祥维纳斯瓦兰佐瑟古律创始人阿都拉萨成立1973年1月1日 (1973-01-01)[1]设立1974年7月1日 (1974-07-01)前身 联盟总部 马来西亚 吉隆坡 50480 秋傑区敦依斯迈路太子世贸中心(英�...

Stasiun Kirihara桐原駅Stasiun Kirihara pada September 2007LokasiTeradomari-gobuichi, Nagaoka-shi, Niigata-ken 959-0154JepangKoordinat37°36′06″N 138°47′33″E / 37.60167°N 138.79250°E / 37.60167; 138.79250Koordinat: 37°36′06″N 138°47′33″E / 37.60167°N 138.79250°E / 37.60167; 138.79250Operator JR EastJalur■ Jalur EchigoLetak36.2 km dari KashiwazakiJumlah peron1 peron sampingJumlah jalur1Informasi lainStatusTanpa stafSitu...

Sanguijuelas Una sanguijuela en un manantial, buscando efímeras bajo los guijarros. Montaje de un ejemplar de Helobdella.TaxonomíaReino: AnimaliaFilo: AnnelidaClase: ClitellataSubclase: HirudineaLamarck, 1818Infraclases y órdenes Acanthobdellida Euhirudinea Arhynchobdellida Rhynchobdellida [editar datos en Wikidata] Los hirudíneos (Hirudinea) son una clase del filo anélidos, conocidos popularmente como sanguijuelas. Hay hirudíneos marinos, terrestres y arborícolas, per...

For keynote presentations given by Steve Jobs, see Stevenote. This list is incomplete; you can help by adding missing items. (August 2022) The Yerba Buena Center for the Arts's exterior prepared in anticipation for the March 2, 2011 unveiling of Apple's iPad 2 Apple Inc. has announced major new and redesigned products and upgrades through press conferences, while minor updates often happen through press releases on Apple Newsroom. The press conferences have historically garnered a significan...

2012 video game 2012 video game007 LegendsDeveloper(s)EurocomPublisher(s)ActivisionWriter(s)Bruce FeirsteinRobin MatthewsComposer(s)David ArnoldKevin KinerSeriesJames Bond video gamesPlatform(s)PlayStation 3Xbox 360Microsoft WindowsWii UReleasePlayStation 3 & Xbox 360NA: 16 October 2012EU: 19 October 2012AU: 31 October 2012Microsoft WindowsWW: 2 November 2012Wii UEU: 7 December 2012NA: 11 December 2012Genre(s)First-person shooterInteractive filmMode(s)Single-player, multiplayer 007 Legend...

A hat used by the Serbs in folk attire Civil šubaras The šubara (Serbian Cyrillic: шубара) is a type of traditional male winter hat used by the Serbs in folk attire. It is in a conical or cylindrical shape predominantly in black colour, because of the black lamb/sheep fur (woollen).[1][2] The šubara is a traditional peasant hat used in harsher and colder times. It was used in World War I by the Serbian soldiers and by the Chetniks in World War II and again during the ...

American musician Les ClaypoolClaypool performing in March 2011Background informationBirth nameLeslie Edward ClaypoolAlso known asColonel ClaypoolBorn (1963-09-29) September 29, 1963 (age 60)Richmond, California, U.S.OriginEl Sobrante, California, U.S.Genres Alternative metal funk metal funk rock progressive rock experimental rock thrash metal Occupation(s) Musician singer songwriter record producer filmmaker author Instrument(s) Bass vocals double bass whamola Years active1984–present...

















